基于压缩感知的三维网格模型数据处理方法与流程

本发明涉及计算机数据压缩领域，尤其涉及一种基于压缩感知的三维网格模型数据处理方法。

背景技术：

三维模型在计算机中表示的方法很多，概括起来有：点云表示、体素表示、参数曲面表示、隐函数表示、多边形网格表示等。目前标准的三维模型表示方式是三角网格模型，这种表示方法结构明确、处理简单、获取容易，是工业界的标准表示方式。三角网格模型的数据结构包括几何结构与拓扑结构。几何结构部分描述了顶点的坐标信息，拓扑结构部分描述了面的组成信息。因为是三角网格，所以拓扑结构部分均为三角面片。计算机中的三维模型是由许多三角形拼接起来的，三角形数量决定了模型的精细程度，也决定了存取数据量的大小，三维模型之所以数据量大，就是由于用于拼接模型的三角形太多。

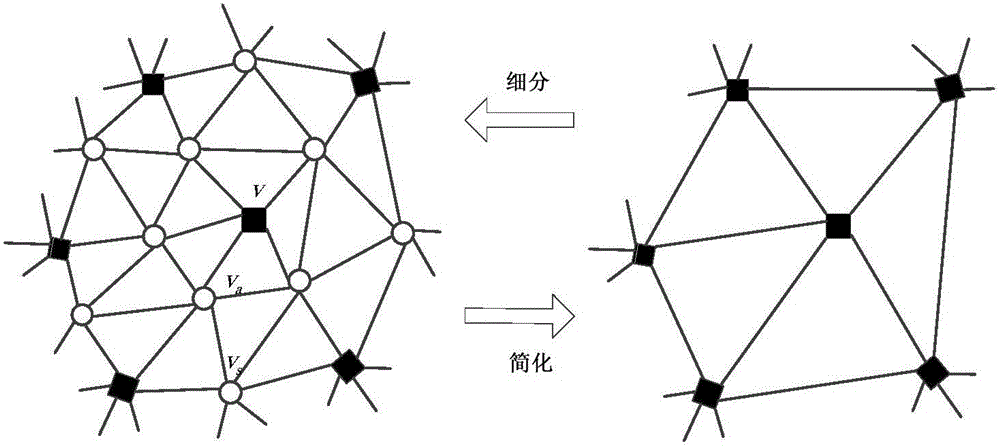
三维模型简化处理的过程就是减少拼接三维模型三角形个数的过程。网格简化是曲面细分的逆过程，也称逆细分。常用的基于三角网格的简化模式有逼近型的逆Loop细分和插值型的逆Butterfly细分等，它们都是对三角形进行面分解操作，按照不同的规则减少细密的网格顶点和三角形数目。附图1表示了曲面细分与网格简化的关系。

随着互联网的不断发展以及人们对三维模型需求的不断增加，当前各种应用对模型的质量要求不断提高，这也接导致了三维模型的数据量不断增大。因此对三维模型进行压缩，使用户快速获得模型，也是急需解决的问题之一。几何模型的压缩方法可以分为单分辨率压缩和渐进压缩，单分辨率压缩尽管能最大限度的保持压缩精度，但这种方法通常不能被移动用户接收，因为只有全部模型数据下载以后图形才能被渲染；渐进压缩可以灵活的、交互式的方式，用户先快速存取轮廓模型，然后边下载细节信息边对模型渐进加细。

随着人们对三维模型数量与质量的要求不断提高，三维模型库中模型的数据规模和复杂程度也随之增加。一方面由于高分辨率的几何模型具有数万个三角形，在短时间内存储和显示如此庞大的数据对移动终端存在很大的压力。另一方面移动终端对图形显示的实时性要求较高，所以经常面临使用者失去等待的耐心的情况；虽然互联网已成为虚拟现实和可视化系统的主流平台，而目前的网络速度远远不能满足大规模三维几何模型实时传输的需求。传统的三维模型简化与压缩方法，压缩比不理想并且需要大量计算，不适合在以上情况下使用。

技术实现要素：

本发明旨在至少解决现有技术中存在的技术问题，特别创新地提出了一种基于压缩感知的三维网格模型数据处理方法。

为了实现本发明的上述目的，本发明提供了一种基于压缩感知的三维网格模型数据处理方法，包括如下步骤：

S1，将需要传送的三维模型数据进行分块；

S2，分块后的三维模型块数据采用改进版Loop模型进行简化处理，对不同三维模型块数据的三角形网格经过逆细分简化；

S3，对基网格的几何结构数据进行串行化，并且对一系列偏移量集串行化；

S4，通过压缩感知方法对基网格和一系列偏移量集进行压缩处理，并将压缩的数据传输到远端，通过数据重构方法进行解压缩，获取原始三维模型数据。

所述的基于压缩感知的三维网格模型数据压缩方法，优选的，所述S1包括：

将全部三维模型按照简单程度或复杂程度分成K块，其中S_k表示第k块；

S1-1，对简单三维模型数据的三维网格进行多次简化，减少大量的三维模型数据网格数目，其中多次简化的数量大于3；

S1-2，对复杂的模块进行1-2次的网格简化。

所述的基于压缩感知的三维网格模型数据压缩方法，优选的，所述S2包括：

对分块后的不同三维模型块的三角形网格进行逆细分简化，生成由基网格和一系列偏移量集组成具有多分辨率的渐进网格；

S2-1，三维模型的三角网格表示成M＝(V,F)，其中V表示几何信息的集合，即网格顶点坐标的集合V_i＝(x_i,y_i,z_i)，F表示网格拓扑信息集合；表示第k块细密的三角形网，表示具有多分辨率的渐进网格，表示第k块的基网格；d^j表示网格M^j+1简化成下一层粗网格M^j后的偏移量集，表示第k块的偏移量集；第k块细密的三角形网简化后表示为Ψ_n×n表示基网格的稀疏矩阵；Φ_m×n表示随机观测矩阵。

所述的基于压缩感知的三维网格模型数据压缩方法，优选的，所述S2还包括：

对三维模型进行简化过程采用改进版Loop模型，对不同模型块的三角形网格经过逆细分简化；

S2-2，将三角形网格中的所有顶点分裂为偶点和奇点，分别归到奇点集和偶点集中；奇异点是需要保留的信息，故首先选奇异点，v点将其设为偶点，与其相邻的顶点v_a设为奇点；对以v为中心，与v_a相邻的对称点v_s设为偶点，这样依次分裂下去，直到将网格中所有的顶点分裂完毕；

S2-3，网格中的顶点分裂成奇点与偶点两个集合后，由于表示几何特征的奇异点归到偶点集合中，故将奇点集作为冗余信息删除，实现三维网格的简化，在删除奇点之前要建立偶点与奇点之间的联系，以便以后的模型重建，采用改版Loop模式作为预测器，计算实际奇点与预测奇点的差值得到偏移量集改进版Loop模型对内部边顶点的计算如下：

改进版Loop模型对边界边顶点的计算如下：

其中v_o表示预测得到的奇点，v₁、v₂、v₃、v₄表示上一层与奇点v_o相关联的邻接点；实际奇点与预测奇点的差值得到偏移量集

网格中每个奇点都会产生一个偏移量，所以是向量，由于网格中邻接顶点之间的位置不会有很大的突变，故偏移量的值很小，多数偏移量趋于0；因此首先设定一个阈值，当偏移量小于阈值时，令其值为0，这样就只有少部分非零数；

S2-4，删除奇点集合奇点集后，剩余的偶点集作为简化后网格的顶点，形成新的网格由于网格中的奇异点都保留下来，故简化后新生网格基本保持着上一层网格的特征；重复以上步骤，将稠密的网格简化为基网格简化后的渐进网格表示为

所述的基于压缩感知的三维网格模型数据压缩方法，优选的，所述S3包括：

S3-1，先将几何结构串行化，即将相同坐标分量X(Y或Z)排成一列，作为一个列矢量；

可以看作是三组分离的一维信号；以下只针对一维信号X进行分析，同样的方法可以应用于Y和Z；

S3-2，由于网格邻接顶点之间的位置不会有很大的突变，故偏移量集中的偏移量多数集中在零值附近，因此首先设定一个阈值δ，当偏移量小于设定阈值δ时，令其值为0，然后将阈值处理后的偏移量集向量排成一列，形成列向量

所述的基于压缩感知的三维网格模型数据压缩方法，优选的，所述S4压缩过程包括：

S4-1，为了得到信号的稀疏表达，引入离散余弦变换，根据公式

其中X_C(u)是第u个余弦变换系数，u是广义频率变量，u＝1,2,…N-1；x(l)是时域N点序列，l＝1,2,…N-1。

因此可得离散余弦变换系数矩阵C：

其中变换矩阵C是一个正交矩阵。

首先考虑对几何信息进行压缩处理，取出的第一列并经过离散余弦变换，信号在离散余弦变换作用下稀疏表示为：

上式中的为信号在新坐标基底下的表达式，Ψ表示稀疏基；是n×1维列向量，经过稀疏变换后，存在个r较大系数值，其他几乎为0，称信号是r稀疏的；同样的方法可以应用于Y和Z，其中表示稀疏后的几何信息；

S4-2，生成随机观测矩阵Φ_m×n，分别对进行观测，即得到观测向量

其中r<<m<<n，根据压缩感知经验公式m≥4r；A^CS表示感知矩阵，Φ_m×n与Ψ_n×n不相干；得到m维的信号，即实现了基网格几何信号的压缩；然后进行一系列偏移量集的压缩；

S4-3，偏移量集经过阈值处理后，多数偏移量为0，因此偏移量集直接具有稀疏性，故采用压缩感知进行数据压缩时，不需要先使用额外稀疏基进行稀疏化，稀疏基用单位矩阵I_n×n表示；生成随机观测矩阵Φ_m×n，对进行进行观测，得到实现偏移量集的压缩。

所述的基于压缩感知的三维网格模型数据压缩方法，优选的，所述S4重建过程包括：

S4-4，渐进网格依次按照在网络中渐进传输；几何模型的重建也是网格简化的逆过程，也是渐进进行的；首先利用

求出然后通过恢复出原来的信号得到几何信息即得到基网格因此可以根据基网格构建轮廓模型；

S4-5，其次利用逐一求出偏移量集并同时利用改进版Loop模式对网格进行细分；新产生的顶点通过偏移量集进行调整，得到网格网格细分后产生的顶点又通过偏移量进行调整；以此类推，直到完全重建第k块模型或获得模型分辨率能满足移动终端的分辨率要求为止。

综上所述，由于采用了上述技术方案，本发明的有益效果是：

本发明有效地压缩原始三维模型的数据并加快数据的传输，满足移动终端存储量小和实时性高的要求。

本发明的附加方面和优点将在下面的描述中部分给出，部分将从下面的描述中变得明显，或通过本发明的实践了解到。

附图说明

本发明的上述和/或附加的方面和优点从结合下面附图对实施例的描述中将变得明显和容易理解，其中：

图1是三维模型示意图；

图2是本发明方法示意图；

图3是本发明方法三维模型几何信息图；

图4是本发明方法具体工作流程图；

图5是本发明方法效果示意图。

具体实施方式

下面详细描述本发明的实施例，所述实施例的示例在附图中示出，其中自始至终相同或类似的标号表示相同或类似的元件或具有相同或类似功能的元件。下面通过参考附图描述的实施例是示例性的，仅用于解释本发明，而不能理解为对本发明的限制。

在本发明的描述中，需要理解的是，术语“纵向”、“横向”、“上”、“下”、“前”、“后”、“左”、“右”、“竖直”、“水平”、“顶”、“底”“内”、“外”等指示的方位或位置关系为基于附图所示的方位或位置关系，仅是为了便于描述本发明和简化描述，而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作，因此不能理解为对本发明的限制。

在本发明的描述中，除非另有规定和限定，需要说明的是，术语“安装”、“相连”、“连接”应做广义理解，例如，可以是机械连接或电连接，也可以是两个元件内部的连通，可以是直接相连，也可以通过中间媒介间接相连，对于本领域的普通技术人员而言，可以根据具体情况理解上述术语的具体含义。

如图2所示，服务端将需要传送的三维模型分成K块，其中S_k表示第k块。几何模型的三角网格可以表示成M＝(V,F)，其中V表示几何信息的集合，即网格顶点坐标的集合V_i＝(x_i,y_i,z_i)，F表示网格拓扑信息集合；表示第k块细密的三角形网，表示具有多分辨率的渐进网格，表示第k块的基网格；d^j表示网格M^j+1简化成下一层粗网格M^j后的偏移量集，表示第k块的偏移量集；第k块细密的三角形网简化后表示为Ψ_n×n表示基网格的稀疏矩阵；Φ_m×n表示随机观测矩阵。具体实施过程如下：

步骤1：开始。

步骤2：对三维模型进行分块处理。将整体三维模型按照复杂简单程度分成K块，其中S_k表示第k块。对简单模块的三维网格进行多次简化，减少大量的三维模型网格数目，其中多次简化的数量大于3；而对复杂的模块只进行1-2次的网格简化，保证能够尽可能的保留原有信息。

步骤3：三维模型的简化。根据步骤2，采用改进版Loop模型，对不同模型块的三角形网格经过逆细分简化。将三维模型第k块较细密的三角形网格逆细分简化，形成具有多分辨率的渐进网格同时生成一系列偏移量如附图1所示，在三角形网格中，定义与六条边相连接的顶点为正则点，非正则的顶点为奇异点，所以附图1中v点为奇异点。所有顶点都是正则点的网格为正则网格，多数顶点是正则点的网格为半正则网格。将第k块较细密的网格简化的具体步骤如下：

(1)将三角形网格中的所有顶点分裂为偶点和奇点，分别归到奇点集和偶点集中。奇异点是需要保留的信息，故首先选奇异点，图1中的v点，并将其设为偶点，与其相邻的顶点v_a设为奇点；对以v为中心，与v_a相邻的对称点v_s设为偶点，这样依次分裂下去，直到将网格中所有的顶点分裂完毕。

(2)网格中的顶点分裂成奇点与偶点两个集合后，由于表示几何特征的奇异点归到偶点集合中，故将奇点集作为冗余信息删除，实现三维网格的简化。在删除奇点之前要建立偶点与奇点之间的联系，以便以后的模型重建。采用改版Loop模式作为预测器，计算实际奇点与预测奇点的差值得到偏移量集改进版Loop模型对内部边顶点的计算如下：

改进版Loop模型对边界边顶点的计算如下：

其中v_o表示预测得到的奇点，v₁、v₂、v₃、v₄表示上一层与奇点v_o相关联的邻接点。实际奇点与预测奇点的差值得到偏移量集

网格中每个奇点都会产生一个偏移量，所以是向量，由于网格中邻接顶点之间的位置不会有很大的突变，故偏移量的值很小，多数偏移量趋于0。因此首先设定一个阈值，当偏移量小于阈值时，令其值为0，这样就只有少部分非零数。

(3)删除奇点集合奇点集后，剩余的偶点集作为简化后网格的顶点，形成新的网格由于网格中的奇异点都保留下来，故简化后新生网格基本保持着上一层网格的特征。重复以上3个步骤，可以将稠密的网格简化为基网格简化后的渐进网格表示为

步骤4：三维模型几何信息可以由图3所示。考虑相邻点的相同坐标分量具有更强的相关性，为了获得更好地压缩效果，本发明先将几何结构串行化，即将相同坐标分量X(Y或Z)排成一列，作为一个列矢量。

可以看作是三组分离的一维信号。以下只针对一维信号X进行分析，同样的方法可以应用于Y和Z。

由于网格邻接顶点之间的位置不会有很大的突变，故偏移量集中的偏移量多数集中在零值附近，因此首先设定一个阈值δ，当偏移量小于设定阈值δ时，令其值为0，然后将阈值处理后的偏移量集向量排成一列，形成列向量。

步骤5：应用压缩感知方法对信号进行处理的前提是信号必须在一组基底下为稀疏信号。为了得到信号的稀疏表达，引入离散余弦变换，根据公式

其中X_C(u)是第u个余弦变换系数，u是广义频率变量，u＝1,2,…N-1；x(l)是时域N点序列，l＝1,2,…N-1。

因此可得离散余弦变换系数矩阵C：

其中变换矩阵C是一个正交矩阵。

首先考虑对几何信息进行压缩处理，取出的第一列并经过离散余弦变换，信号在离散余弦变换作用下稀疏表示为：

上式中的为信号在新坐标基底下的表达式，Ψ表示稀疏基；是n×1维列向量，经过稀疏变换后，存在个r较大系数值，其他几乎为0，称信号是r稀疏的；同样的方法可以应用于Y和Z，其中表示稀疏后的几何信息；

生成随机观测矩阵Φ_m×n，分别对进行观测，即得到观测向量

其中r<<m<<n，根据压缩感知经验公式m≥4r；A^CS表示感知矩阵，Φ_m×n与Ψ_n×n不相干；得到m维的信号，即实现了基网格几何信号的压缩；然后进行一系列偏移量集的压缩。

如图4所示，步骤4中偏移量集经过阈值处理后，多数偏移量为0，因此偏移量直接具有稀疏性，故采用压缩感知进行数据压缩时，不需要先使用额外稀疏基进行稀疏化，稀疏基用单位矩阵I_n×n表示。生成随机观测矩阵Φ_m×n，对进行进行观测，得到实现偏移量集的压缩。

步骤6：渐进网格依次按照在网络中渐进传输；几何模型的重建也是网格简化的逆过程，也是渐进进行的；首先利用

求出然后通过恢复出原来的信号得到几何信息即得到基网格因此可以根据基网格构建轮廓模型；

S4-5，其次利用逐一求出偏移量集并同时利用改进版Loop模式对网格进行细分；新产生的顶点通过偏移量集进行调整，得到网格网格细分后产生的顶点又通过偏移量进行调整；以此类推，直到完全重建第k块模型或获得模型分辨率能满足移动终端的分辨率要求为止。

步骤7：结束。

如图5所示，本发明提出的基于压缩感知的三维网格模型数据处理方法能够精确的重构原始数据，对于基网格的重构也是如此。而在三维模型数据压缩和传输方面，首先采用改进的Loop模型简化，降低了基网格数目，然后通过压缩感知进行采样压缩并传输，进一步降低了传输数据，在获得较高压缩比的同时，运行速度较快，满足移动终端存储量小和实时性高的要求。

在本说明书的描述中，参考术语“一个实施例”、“一些实施例”、“示例”、“具体示例”、或“一些示例”等的描述意指结合该实施例或示例描述的具体特征、结构、材料或者特点包含于本发明的至少一个实施例或示例中。在本说明书中，对上述术语的示意性表述不一定指的是相同的实施例或示例。而且，描述的具体特征、结构、材料或者特点可以在任何的一个或多个实施例或示例中以合适的方式结合。

尽管已经示出和描述了本发明的实施例，本领域的普通技术人员可以理解：在不脱离本发明的原理和宗旨的情况下可以对这些实施例进行多种变化、修改、替换和变型，本发明的范围由权利要求及其等同物限定。