纸样规格参数推理模型的神经网络的训练学习方法和系统与流程

本发明属于神经网络学习领域，尤其涉及一种纸样规格参数推理模型的神经网络的训练学习方法和系统。

背景技术：

人工神经网络(artificialneuralnetwork，即ann)，是20世纪80年代以来人工智能领域兴起的研究热点[32]。信息处理角度对人脑神经元网络进行抽象，建立某种简单模型，按不同的连接方式组成不同的网络[33]。bp(back-propagation)神经网络模型是人工神经网络模型领域运用最广的一种，也是人工神经网络领域的精髓。因为bp神经网络的中间层一般为一层或者多层，所以整个网络层为三层或者三层以上。

神经网络在投入使用之前或投入使用之后需要进行训练学习以满足神经网络根据输入值输出较准确的输出值，但是现有技术的神经网络训练学习方法不够灵活导致存在误差较大，以及训练速率不合适导致网络训练效果不佳等问题。

为了解决上述技术问题，人们进行了长期的探索，例如中国专利公开了一种基于深层神经网络的声学模型训练方法、主机和系统[申请号：cn201310704701.9]，其方法包括：主控主机将原始深层神经网络的各副本深层神经网络下发给至少一个运算主机，以指示运算主机基于训练数据对副本深层神经网络进行训练；主控主机定时查询各所述运算主机的状态，若查询到处于训练停止状态的运算主机，获取停止状态运算主机上副本深层神经网络的加权参数的变化量；主控主机根据所述停止状态运算主机上副本深层神经网络的加权参数的变化量，更新主控主机上原始深层神经网络的加权参数；主控主机利用更新后的原始深层神经网络的加权参数绝对值更新所述停止状态运算主机上副本深层神经网络的加权参数绝对值。

上述方案通过利用至少一个运算主机对副本深层神经网络进行训练，使得能够利用多台主机异步、并行的进行深层神经网络训练，大幅提高了深层神经网络训练的效率，但是仍然存在需要改进的地方，例如，训练方法仍然不够灵活、训练速率仍然不合适等。

技术实现要素：

本发明的目的是针对上述问题，提供一种提高学习效果的纸样规格参数推理模型的神经网络的训练学习方法；

本发明的另一目的是针对上述技术问题，提供一种基于纸样规格参数推理模型的神经网络的训练学习方法的用于纸样规格参数推理模型的神经网络训练学习的神经网络训练系统。

为达到上述目的，本发明采用了下列技术方案：

本发明的纸样规格参数推理模型的神经网络的训练学习方法，包括以下步骤：

s1：在输入层导入包括网络输入向量和网络目标向量的多组学习样本后将输出层连接权、中间层连接权、中间层输出阈值和输出层输出阈值进行初始化设置；

s2：随机选取一组学习样本，并基于选取的学习样本、中间层连接权和中间层输出阈值通过中间层算法计算中间层各单元的输入和中间层各单元输出；

s3：基于输出层连接权、输出层输出阈值和步骤s2中得到的中间层各单元的输出通过输出层算法计算输出层各单元的输出和输出层各单元的响应；

s4：根据网络目标向量和网络输出层各单元的响应计算输出层各单元的输出层一般化误差，并基于输出层连接权、输出层一般化误差和中间层的输出通过中间层一般化误差算法计算中间层各单元的中间层一般化误差；

s5：根据输出层一般化误差和中间层的输出通过输出层连接权修正算法修正输出层连接权，通过输出层输出阈值修正算法修正输出层输出阈值；根据中间层一般化误差和网络输入向量通过中间层连接权修正算法修正中间层连接权，通过中间层输出阈值修正算法修正中间层输出阈值；

s6：随机选取下一组学习样本并返回步骤s2，直至选取至最后一组学习样本和/或网络全局误差一般化误差小于一个设定阈值。

在上述的纸样规格参数推理模型的神经网络的训练学习方法中，在步骤s2之前，还包括以下步骤：

神经网络自行设定和选取和/或接收用户设置的包括输入层节点、输出层节点、中间层层数、中间层节点、激活函数、初始权值和学习速率中的任意一种或多种组合的训练参数。

在上述的纸样规格参数推理模型的神经网络的训练学习方法中，所述的输入层节点为人体多个部位尺寸的向量，所述的输出层节点为成衣多个部位尺寸的向量，所述的中间层层数设定为一层、二层或三层，所述的中间层节点通过试值的方式和/或通过经验式进行选取，所述的激活函数包括中间层激活函数和输出层激活函数，且中间层激活函数选取sigmoid函数，输出层激活函数选取purelin线性函数，初始权值由matlab随机产生，学习速率选取0.01-0.8。

在上述的纸样规格参数推理模型的神经网络的训练学习方法中，所述的经验式包括至少三种：

h＝2i+1①

h＝log2ii∈(0.02i，4i)③

h：中间层节点数；

i：输入层节点数；

o：输出层节点数；

a：常数。

在上述的纸样规格参数推理模型的神经网络的训练学习方法中，所述的学习速率为变化的自适应学习速率，神经网络根据训练的不同阶段自动设置不同学习速率的大小。

在上述的纸样规格参数推理模型的神经网络的训练学习方法中，在步骤s1中，所述的网络输入向量为人体多个部位尺寸，即：pk＝(a1，a2，...，an)

k：学习样本数量；n：输入层节点个数；

所述的网络目标向量为对应人体的成衣的多个部位尺寸，即

tk＝(s1，s2，...，sqq：输出层节点个数；

在步骤s2中，所述的中间层算法为公式④，即

其中，

sj：中间层各单元的输入；

wij：输入层至中间层的中间层连接权，wij，i＝1，2，…，n；j＝1，2，…，p；

θj：中间层各单元的中间层输出阈值；θj，j＝1，2，…，p；

bj：中间层各单元的输出；

ai：第i个网络输入向量。

其中，n：输入层节点个数；p：中间层节点个数

在上述的纸样规格参数推理模型的神经网络的训练学习方法中，在步骤s3中，所述的输出层算法为公式⑤，即

其中，

lt：输出层各单元的输出；

vjt：输出层连接权，vjt，j＝1，2，…，p；t＝1，2，…，q；

yt：输出层输出阈值；

bj：中间层各单元的输出；

ct：输出层各单元的响应；

p：中间层节点个数；q：输出层节点个数。

在上述的纸样规格参数推理模型的神经网络的训练学习方法中，在步骤s4中，所述的输出层一般化误差通过网络目标向量与输出层的响应作差而得，即：

输出层一般化误差；

tk：网络目标向量：

ct：输出层响应；

所述的中间层一般化误差算法为公式⑥，即

中间层一般化误差；

dt：输出层一般化误差。

在上述的纸样规格参数推理模型的神经网络的训练学习方法中，在步骤s5中，所述的输出层连接权修正算法为公式⑦，输出层输出阈值修正算法为公式⑧

t＝1，2，…，q，j＝1，2，…，p，0<a<1；

vjt(n)：前一个输出层连接权；

vjt(n+1)：前一个输出层连接权经过修正后的下一个输出层连接权；

yt(n)：前一个输出层输出阈值；

yt(n+1)：前一个输出层输出阈值经过修正后的下一个输出层输出阈值；

所述的中间层连接权修正算法为公式⑨，所述的中间层输出阈值修正算法为公式⑩，即

i＝1，2，…，n，j＝1，2，…，p，0<β<1

wij(n)：前一个中间层连接权；

wij(n+1)：前一个中间连接权经过修正后的下一个中间层连接权；

θj(n)：前一个中间层输出阈值；

θj(n+1)：前一个中间层输出阈值经过修正后的下一个中间层输出阈值。

一种基于纸样规格参数推理模型的神经网络的训练学习方法的用于纸样规格参数推理模型的神经网络训练学习的神经网络训练系统。

本发明纸样规格参数推理模型的神经网络的训练学习方法和系统相较于现有技术具有以下优点：1、得到一个能够根据人体尺寸得出成衣尺寸的神经网络系统，实现从人体尺寸到连衣裙成衣尺寸的映射；2、通过参数的选择和与实际样本比较的方法，使训练学习后的神经网络的输出结果更加接近实际值；3、通过沿系统平均误差的反方向修改权值，使网络逐步收敛，提高学习训练效果；4、训练过程灵活，且选取的参数均适合于神经网络的训练需要，提高训练效果。

附图说明

图1是本发明的神经网络学习训练方法流程图；

图2是本发明参数确定方法的流程图；

图3是本发明三层神经网络模型图；

图4是本发明sigmoid函数图像；

图5是本发明purelin函数图像；

图6是本发明神经网络训练过程图。

具体实施方式

以下是本发明的优选实施例并结合附图，对本发明的技术方案作进一步的描述，但本发明并不限于这些实施例。

本发明的纸样规格参数推理模型的神经网络的训练学习方法，bp神经网络的训练学习：训练网络的学习阶段，给定模式作为网络的输入，要求网络通过调节所有的连接权和各神经元的阈值，使得在输出层神经元上得到需要的理想输出，一旦网络完成这种调节，则再给出另一个输入模式并有相应的理想输出，要求网络继续完成对这组模式的学习，这实际上就是要求网络寻找单一的一组连接权系数和偏置，以满足给定的所有输入输出模式对。为了使网络逐步收敛，沿系统平均误差的反方向修改权系数的值。

下面先对本实施例需要用到参数进行介绍：

网络输入向量pk＝(a1，a2，…，an)

网络目标向量tk＝(s1，s2，…，sq)

中间层单元输入向量sk＝(s1，s2，…，sp)，输出向量

bk＝(b1，b2，…，bp)

输出层单元输入向量lk＝(l1，l2，…，lq)，输出向量

ck＝(c1，c2，…，cq)

参数k＝1，2，…，m，表示样本数据的个数

中间层连接权，即输入层至中间层的连接权wij，i＝1，2，…，

n；j＝1，2，…，p；

输出层连接权，即中间层至输出层的连接权vij，vjt，j＝

1，2，…，p；t＝1，2，…，q；

中间层各单元的输出阈值θj，j＝1，2，…，p；

输出层各单元的输出阈值yt，t＝1，2，…，q。

如图1所示，神经网络学习训练的方法具体包括如下步骤：

s1：初始化：在输入层导入包括网络输入向量和网络目标向量的多组学习样本后将输出层连接权、中间层连接权、中间层输出阈值和输出层输出阈值进行初始化设置，给每个连接权值wij、vjt，阈值θj与yt赋予区间(－1，1)内的随即值；

s2：随机选取一组学习样本：并基于选取的学习样本、中间层连接权wij和中间层输出阈值θj通过中间层算法计算中间层各单元的输入和中间层各单元输出，

中间层算法公式为④：

其中，中间层各单元的输出bj又通过中间层各单元的输入sj通过传递函数计算而得；

bj＝f(sj)j＝1，2，…，p

其中，

sj：中间层各单元的输入；

wij：输入层至中间层的中间层连接权，wij，i＝1，2，…，n；j＝1，2，…，p；

θj：中间层各单元的中间层输出阈值；θj，j＝1，2，…，p；

bj：中间层各单元的输出；

ai：第i个网络输入向量；

其中，n：输入层节点个数；p：中间层节点个数。

s3：基于输出层连接权、输出层输出阈值和步骤s2中得到的中间层各单元的输出通过输出层算法计算输出层各单元的输出和输出层各单元的响应；

输出层算法为公式⑤，即

同样地，利用传递函数计算输出层各单元的响应ct：

ct＝f(lt)t＝1，2，…，p；

其中，

lt：输出层各单元的输出；

vjt：输出层连接权，vjt，j＝1，2，…，p；t＝1，2，…，q；

yt：输出层输出阈值；

bj：中间层各单元的输出；

ct：输出层各单元的响应；

p：中间层节点个数；q：输出层节点个数。

s4：根据网络目标向量网络输出层各单元的响应ct，计算输出层各单元的输出层一般化误差并基于输出层连接权vjt、输出层一般化误差dt和中间层的输出bj，通过中间层一般化误差算法计算中间层各单元的中间层一般化误差

其中，输出层一般化误差通过网络目标向量与输出层的响应做差而得，即：

输出层一般化误差；

tk：网络目标向量：

ct：输出层响应；

进一步地，中间层一般化误差算法为公式⑥，即

中间层一般化误差；

dt：输出层一般化误差。

在计算输出层的一般化误差后，执行步骤s5：

s5：根据输出层一般化误差和中间层的输出bj，通过输出层连接权修正算法修正输出层连接权vjt，通过输出层输出阈值修正算法修正输出层输出阈值γt；根据中间层一般化误差和网络输入向量pk＝(a1，a2，...，an)，通过中间层连接权修正算法修正中间层连接权wij，通过中间层输出阈值修正算法修正中间层输出阈值θj；

其中，输出层连接权修正算法为公式⑦，输出层输出阈值修正算法为公式⑧，中间层连接权修正算法为公式⑨，中间层输出阈值修正算法为公式⑩，

t＝1，2，…，q，j＝1，2，…，p，0<a<1；

vjt(n)：前一个输出层连接权；

vjt(n+1)：前一个输出层连接权经过修正后的下一个输出层连接权；

yt(n)：前一个输出层输出阈值；

yt(n+1)：前一个输出层输出阈值经过修正后的下一个输出层输出阈值；

i＝1，2，…，n，j＝1，2，…，p，0<β<1

wij(n)：前一个中间层连接权；

wij(n+1)：前一个中间连接权经过修正后的下一个中间层连接权；

θj(n)：前一个中间层输出阈值；

θj(n+1)：前一个中间层输出阈值经过修正后的下一个中间层输出阈值。

s6：随机选取下一组学习样本并返回步骤s2，再一次通过步骤s2-s5对连接权与阈值进行修正，直至选取至最后一组学习样本和/或网络全局误差e一般化误差小于一个设定阈值ε，该设定阈值ε极小，例如0.1或0.5等，该设定阈值即本bp神经网络的网络收敛。本实施例中的网络全局误差即为目标值与实际输出的误差平方和。

当所有的训练样本训练结束，但是最后的输出层一般化误差仍然大于设定阈值，则重新从学习样本中随机选取一组学习样本，返回步骤s2继续进行学习。

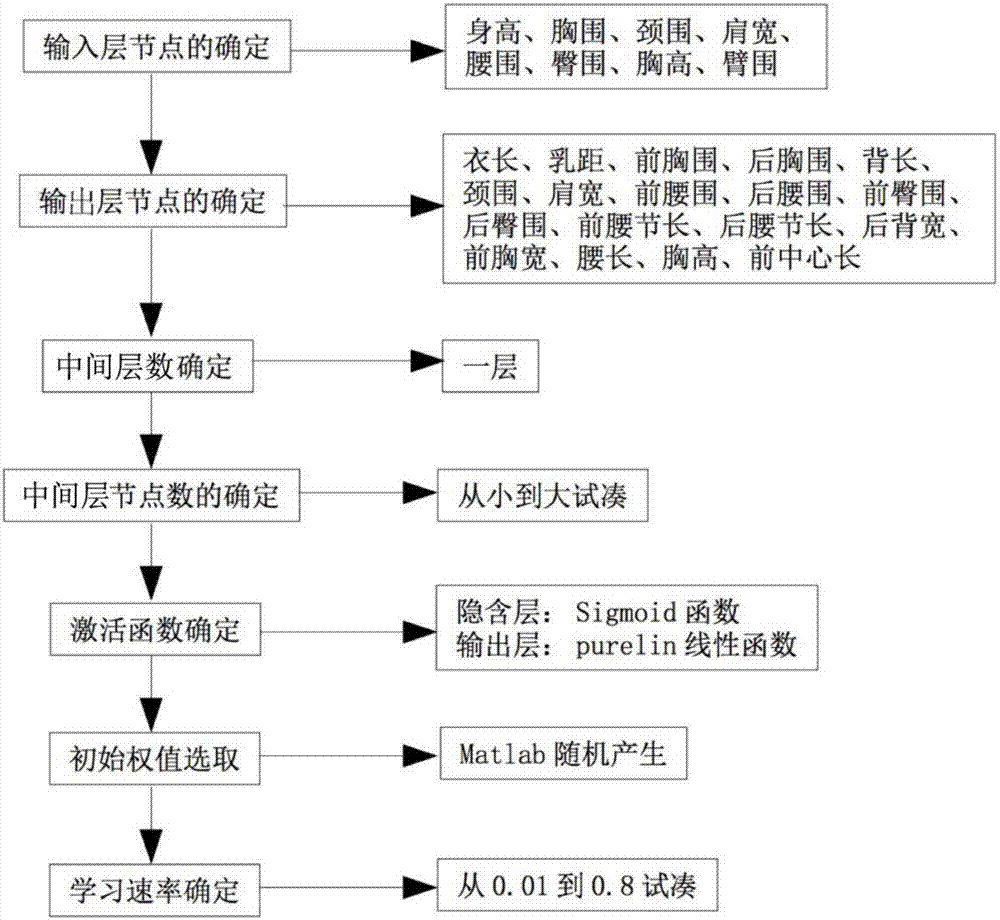
进一步地，如图2所示，在步骤s2之前，还包括以下步骤：

神经网络自行设定和选取和/或接收用户设置的包括输入层节点、输出层节点、中间层层数、中间层节点、激活函数、初始权值和学习速率中的任意一种或多种组合的训练参数，此处的初始权值包括中间层连接权值和输出层连接权值。

其中，gb/t6160标准中对人体测量标准做了详细解释，服装人体测量主要表现在纵向长度的和横向围度的两个方面共25个测量指标，其中长度主要包括身高、前腰节长、后腰节长、臀高、腰高等17个纵向指标，维度包括胸围、腰围、臀围等8个水平指标。但在合体连衣裙制作时主要控制部位包括身高、胸围、颈围、腰围、肩宽、臀围、胸高、臂围8个部位，输入层节点为人体多个部位尺寸的向量，本实施例采用生活装连衣裙进行具体说明，由于从款式结构或合体度上生活装连衣裙均和合体连衣裙的特征相似，所以本实施例将上述8个人体尺寸作为bp神经网络输入层节点。

同样地，输出层节点为成衣多个部位尺寸的向量，输出层的数量以及输出层指标的确定主要是结合实际情况来加以确定。本实施例中输出层向量就是成衣尺寸，由于成衣完整的样板共需衣长、乳间距、前胸围、后胸围、背长、颈围、肩宽、前腰围、后腰围、前臀围、后臀围、前腰节长、后腰节长、后背宽、前胸宽、腰长、胸高和前中心长18个成衣尺寸，所以本实施例的输出层节点采用上述18个向量。

由于神经网络的许多特性就是因为有了中间层的存在才具备的，但是中间层的确定还没有统一的规律可循，建立不同的模型，不同实际运用，中间层的网络结构差异很大。1989年roberthechtnielson在理论上证明了对任意闭合区间连续函数都可以用一个含有中间层的bp网络来逼近，因此一个3层bp网络可以完成任意的n维到m维的映射，3层以上的网络模型虽然训练速度较快，但是随着中间层层数的增加，误差反向传播的计算过程也将变得更加复杂且训练时间更长，而且在模型构建过程中，训练速度可以通过增加中间层的节点数进行控制，所以中间层的层数的多少对于输出结果误差的精度而言并没有太大的影响，所以根据上述理论，可以发现一层中间层的网络模型就符合本实施例的需要，所以本实施例采用一层中间层的网络模型。

由于本实施例的中间层采用一层，所以本实施例神经网络模型为最基本的三层，也就是输入层、中间层和输出层三层，三层的神经网络模型如图3所示。

由于中间层节点数过多或者过少都会对神经网络的模型的实现产生影响，最终导致学校能力不够或者能力下降。如果中间层的节点数在设置时过少，那么相应的学习时间也就比较短，就会因为训练不足而造成网络性能不好；如果中间层节点过多会使得学习时间增加，存储容量变大，训练会陷入局部极小点而得不到最优点。基于上述原因，本实施例的中间层节点数通过试值的方式和/或通过经验式进行选取，其中本实施例的经验式包括至少三种：

h＝2i+1①

h＝log2ii∈(0.02i，4i)③

h：中间层节点数；

i：输入层节点数；

o：输出层节点数；

a：常数。

通过试值的方式选取中间层：首先先选择较小的节点数，然后在此基础上将中间层的节点数稍有增大，对两个不同的节点数进行分析选取更优的结果作为中间层的节点数。

为了更好地选择节点数，本实施例结合试值和经验公式两种方法，对学习时间、误差值平方和、收敛速度等网络性能进行综合比较分析，本实施例将中间层节点数设置为12。

误差在反向调节过程中，激活函数是求解误差梯度的重要参数。较为常用的激活函数主要有tansig、logsig、purelin三种。由于s型函数是可微的满足传递函数必须可微的基本条件，故一般选其作为传递函数，s型函数包括sigmoid函数和正切函数，sigmoid函数的值域范围为(0，1)，sigmoid函数：f(x)＝(1+e^-αx)^-1α为常数正切函数的值域为(-1,1)，正切函数：(-1<f(x)<1)

因为sigmoid函数连续可微，能够表现非线性函数的逼近能力，且更加接近于生物神经元的信号输出形式，所以本实施例的中间层激活函数采用sigmoid函数，函数图像如图4所示。

因为sigmoid函数和正切函数的值域在(0，1)或者(-1，1)上，所以对于输出层如果选用s型函数，输出层的输出值将被限制在(0，1)或者(-1，1)的范围内，由于本实施例实际输出值是成衣尺寸，选用s型函数不能满足实际需要，所以本实施例选用purelin线性函数作为输出层激活函数，purelin线性函数图像如图5所示。

进一步地，初始权值由matlab随机产生选取不同的初始权值，不会影响网络的收敛精度，但有可能造成网络在某一局部极小值周围徘徊不出。权值太大还会导致神经元易于进入饱和状态，所以最终训练连接权值在[-10，10]范围内为宜。从全局的观点来看，影响网络训练的因素除初始权值外，还有很多因素，如学习速率和动量项的设定、网络结构及激活函数的选择等，在其它因素一定的条件下，本实施例选择权值初始值的范围为±0.5左右。

进一步地，学习速率值的大小对学习过程的稳定产生重要影响，学习速率如果较大将会使得权值的修正量增大，甚至会出现权值超出最小值的现象；学习速率如果较小会使得学习时间较长，而且不一定收敛，所以为了保证训练过程最终收敛，一般会将学习速率设置为较小值。

一个bp神经网络会对应一个最优的学习效率，本实施例采用从0.01至0.8试凑的方式确定最优的学习速率。

本实施例采用matlab7.0软件对网络进行训练，网络的训练过程图如图6所示

本实施例的网络训练部分程序：

net＝train(net,inputn,outputn)；

inputweights＝net.iw{1,1}；

layerweights＝net.lw{2,1}；

bias1＝net.b{1}；

bias2＝net.b{2}；

savenet；

训练集测试结果对比程序：

figure(i)

subplot(2,1,1)

plot(yy(i,:),'r*-')

holdon

plot(output_train(i,:),'bo')

legend

gridon

xlabel

ylabel(style)

string_1＝{'训练集预测结果对比'；}；

title(string_1)

subplot(2,1,2)

plot(output_test(i,:)-yn(i,:),'r-*')

gridon

xlabel('样本编号')

ylabel('训练结果误差')

string_2＝{'预测值与实际值误差'；}；

title(string_2)；

end

由于本实施例的中间层激活函数采用sigmoid函数，其取值范围介于-1到1之间，因此在网络训练之前需要对样本输入信号进行归一化处理，使得所有样本的输入信号其均值接近于0或与其均方差相比很小，matlab软件中提供了三种常用的数据归一化方法：

(1)利用premnmx、postmnmx、tramnmx函数对数据归一化

(2)利用prestd、poststd、trastd函数对数据归一化

(3)利用matlab语言用户自定义

本实施例对样本归一化处理时选用premnmx、postlnnmx、tramnmx函数，在premnmx函数的调用格式：

[pn,minp,maxp,tn,mint,maxt]＝premnmx(p,t)

p是原始输入数据，t为原始输出数据。pn为归一化处理之后的输入数据，tn是输出数据。n和tn分别是归一化处理之后的输入输出数据，同时返回输入样本p的最大值和最小值，以及输出样本t的最大值和最小值。

进一步地，本实施例还公开了一种用于纸样规格参数推理模型的神经网络训练学习的神经网络训练系统。

本文中所描述的具体实施例仅仅是对本发明精神作举例说明。本发明所属技术领域的技术人员可以对所描述的具体实施例做各种各样的修改或补充或采用类似的方式替代，但并不会偏离本发明的精神或者超越所附权利要求书所定义的范围。

尽管本文较多地使用了输入层、中间层、输出层、连接权、输出层一般化误差、中间层一般化误差等术语，但并不排除使用其它术语的可能性。使用这些术语仅仅是为了更方便地描述和解释本发明的本质；把它们解释成任何一种附加的限制都是与本发明精神相违背的。