一种无人机自主寻路策略方法与流程

本发明主要涉及基于遗传蚂蚁算法的无人机自主寻路策略。
背景技术：
：无人机今年来得到大力的发展，主要应用于地质探测、影视摄影、环境监控、物体跟踪等方面。无人机除了人工控制，还具有自主智能搜索功能，能根据环境障碍物进行智能躲避和最优路径选择。目前较常使用的，通过对障碍物分类进行全局路径规划，主要步骤包括环境建模和寻路策略算法。近来环境建模较多使用时通过栅格法建模，即通过对整体空间划分成不同栅格，没有障碍物的栅格为自由栅格，存在障碍物的非自由栅格。寻路策略算法即是在起点和目标终点之间只能选择最短路径的自由栅格组合。目前通常使用的是将x-y-z三维坐标系空间按一定距离平面进行划分成多个栅格空间，这种方法简单易行，但随着栅格数的增加，搜索组合数存在指数增加极大的耗费了计算资源造成响应慢；而基于遗传蚂蚁算法的寻路策略是借鉴自然选择和自然遗传机制的随机搜索算法，包括选择保留精英算法(elitistgeneticalgorithm,ega)和最大最小蚁群系统(max-minantsystem)，其基本思想在每次迭代中保留适应值最优的个体，该算法一定程度上提高了搜索效率，但仍存在着在算法后期搜索效率降低的问题；最大最小蚁群系统(max-minantsystem)是由德国学者thomasstutzle提出改进的蚁群算法，主要改进如下：并不是对所有的蚂蚁都进行信息要素更新，，只对一只蚂蚁的信息素进行更新，这只蚂蚁只能是当前循环下找到的最优解蚂蚁或可能发现已知最优路径的蚂蚁；同时为了防止某条路径上的信息素出现过大或过小，设定了信息素浓度区间，同时为了开始吸引更多蚂蚁进行搜素，信息素浓度初始化的值设定为区间值，而非常数。但单纯的mmas算法仍然存在搜素效率不高，最优解求解时间过长的问题。技术实现要素：发明目的：为了克服现有技术中存在的不足，本发明提供了一种无人机自主寻路策略方法，通过极坐标系进行环境建模大大减少了计算量，同时通过mmas和ega算法进行快速收敛算法，提高了最优解的搜索效率。技术方案：为实现上述目的，本发明采用以下技术：一种无人机自主寻路策略方法，其特征在于包括以下步骤：(1)基于极坐标系对环境进行建模，首先将无人机等效为质点，将障碍物的体积等效为自身体积与无人机体积之和，在水平面上采用极坐标方式建立扇形栅格划分单元，无人机所在坐标s(t)为t+1时刻的极点；然后在三维环境中，在无人机的运动方向上按照极径距离对各障碍物进行聚类划分，将极径ρ方向上间距小于无人机机长1.2倍的障碍物聚为一类，并记为聚类结果n,n＝1,2,3…n,同时在聚类结果n离无人机质点极径最小和最大处作虚拟环形柱面，从而得到2n+1个子区间；(2)然后通过最大最小蚁群算法mmas得到部分优化解，并作为ega算法的初始值；(3)利用mmas和ega算法进行同步运算，实现路径寻优；最后利用改进的变异算子和mmas继续寻优，最终得到最优路径。进一步改进，步骤(2)中，先进行参数初始化，参数包括蚂蚁数量m1，挥发系数ρ，种群数量m2，交叉概率pc，变异概率pm，最大迭代次数iter_max，信息素重要程度因子α，启发函数重要程度因子β，初始化时迭代次数iter设置为1；然后通过迭代最优解定义算法的转换时刻，并将转换时刻mmas的路径求解值和全局最优求解值作为ega算法的初始解。进一步的，步骤3中mmas和ega算法路径寻优方法包括以下步骤：首先，通过mmas算法继续最优解的计算，并以上次迭代得到的最优解对路径信息素浓度进行更新，计算公式入使(1)式中，τij(t)为t时刻ij两栅格间的信息素浓度，ρ为挥发系数，为迭代最优解的信息素浓度增量；同时，将ega算法每次迭代得到的最优解更新至信息素浓度，加快收敛速度和扩大收敛范围。进一步的，所述障碍物的体积在极径上的长度等效为自身长度和无人机长度之和。进一步的，无人机经过障碍物的最短安全距离为路径与障碍物边缘的最小距离为无人机长度的0.2～0.5倍。有益效果：与现有技术相比，本发明采用全新的极坐标系进行区域环境划分和建模，在确保计算精度的同时简化了计算量，从而提高了寻优效率；同时采用mmas算法与ega算法的收敛速度的特点，采取了在每次中将迭代最优解和ega优化得到的最优解共同更新信息素的方法，提高了搜索最优解的效率附图说明图1为本发明所述无人机自主寻路策略方法的流程示意图。具体实施方式下面结合附图对本发明作更进一步的说明。应当指出：对于本
技术领域：
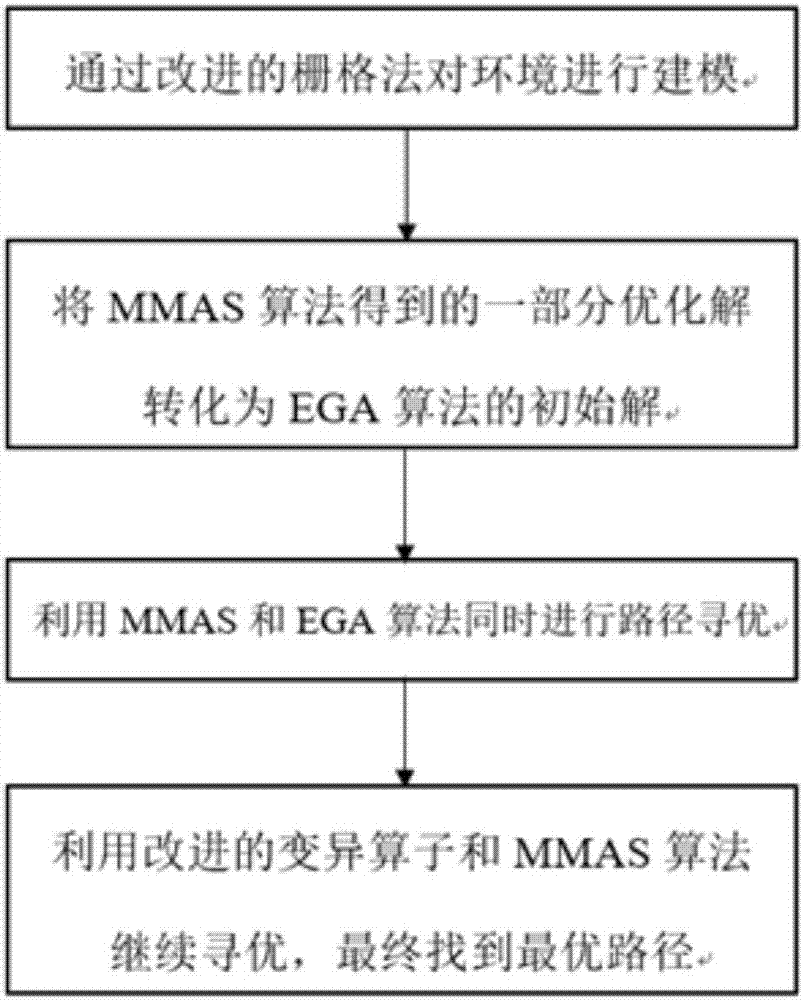
的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。如图1所示，本发明中无人机自主寻路策略方法的路径规范步骤如下：通过极坐标法改进栅格对环境进行建模，将mmas算法得到的部分优化解作为ega算法的初始解，利用mmas和ega算法的同步运算，并结合变异算子继续寻优，最终得到最优路径。具体过程如下：首先，基于极坐标系对环境进行建模，首先将无人机等效为质点，将障碍物的体积等效为自身体积与无人机体积之和，在水平面上采用极坐标方式建立扇形栅格划分单元，无人机所在坐标s(t)为t+1时刻的极点；然后在三维环境中，在无人机的运动方向上按照极径距离对各障碍物进行聚类划分，将极径ρ方向上间距小于无人机机长1.2倍的障碍物聚为一类，并记为聚类结果n,n＝1,2,3…n,同时在聚类结果n离无人机质点极径最小和最大处作虚拟环形柱面，从而得到2n+1个子区间。相对于x-y坐标系下的栅格建模，本发明中的极坐标环境建模越靠近无人机质点，划分区域越小，也就是越精细提高了数据计算精度，随着原理无人机质点，单个划分区域逐渐增大，从而能减少栅格数量和计算量，提高了计算和寻优的计算效率。因此本发明采用近程有限精度计算，远程有限效率计算，从而在保证计算精度的同时，大大减少了计算量，从而提高了计算效率。然后，对mmas和ega算法的参数初始化，包括蚂蚁数量m1，挥发系数ρ，种群数量m2，交叉概率pc，变异概率pm，最大迭代次数iter_max，信息素重要程度因子α，启发函数重要程度因子β，初始化时迭代次数iter设置为1。本发明中在水平面上的路径选择，主要考虑无人机的路径的偏转角和行进长度仅为二维环境下的运动，相对于x-y栅格，路径转变过程时采用的对角线路径，因此相对直接路径更短，同时只需再考虑在高度方向上避开与障碍物的碰撞。然后通过迭代最优解定义算法的转换时刻，并将转换时刻mmas的路径求解值和全局最优求解值作为ega算法的初始解。具体而言：每次迭代中利用mmas算法得到路径解，蚂蚁k在栅格i选择下一个栅格j的转移公式如下：式中，allowedk为蚂蚁k待访问的栅格的集合，对迭代最优解对应的路径进行信息素更新，计算每次迭代的解的平均值、全局最优解和迭代最优解。在i3-3220和4g内存的硬件条件下，利用matlab进行模拟仿真，设定仿真迭代次数为50，按照极角*极长*高度模式建立360*500*500的栅格环境明显，通过本发明算法和传统gaaa算法进行路径规划。仿真结果比较如下性能指标本发明gaaa出现全局最优解仿真次数3012第一次出现最优解时间，s6.810.2平均运行时间20.823.5通过结果比较，可知本发明的寻优能力明显更优秀。当前第1页12