一种基于最优化估计的摄像机外参数标定方法与流程

本发明属于计算机视觉领域，具体涉及一种基于最优化估计的摄像机外参数标定方法。

背景技术：

摄像机外参数标定是计算机视觉应用问题的核心内容，包括运动分割、物体识别和模型校准等。摄像机的外参数是指摄像机相对于世界坐标系的方位，包括选择矩阵r和平移矢量c。摄像机外参数标定就是给定一系列三维点以及对应的图像点，确定r和c。在不存在噪声时，可以采用直接线性变换(dlt)算法求得摄像机外参数，这种方法是利用线性算法求出初始解，然后进行非线性优化。虽然该方法比较有效，但是由于问题的非凸性而往往陷入局部最优。为了求得全局最优解，一些基于重投影误差的l∞范数的全局优化算法已经提出，然而，这些算法是在假设摄像机的旋转矩阵r已知的情况下，仅仅确定摄像机的位置c。

olsson提出了摄像机外参数标定问题的第一种全局优化算法，这种方法是基于全局优化理论，在重投影误差的二范数下采用凸松弛结合分支定界法求解，但其缺点是收敛速度很慢。enqvist利用经典几何的一个简单结论推导l∞范数的必要条件，并将其应用到分支定界方法中进行寻优和检测外围点。该方法的缺点是分支定界方法的寻优区域很难定义。另外一种求取摄像机最优位姿的方法是在旋转空间寻优，通过解一系列的二阶锥规划问题得到最优解，其寻优空间是可以确定的，但是收敛速度仍然较慢。

技术实现要素：

针对现有技术的不足，本发明提出了一种基于最优化估计的摄像机外参数标定方法。

本发明的技术方案为：

一种基于最优化估计的摄像机外参数标定方法，包括以下步骤：

(1)将内参数矩阵已知的被测摄像机固定，并拍摄一个空间结构已知的三维物体的图像；

(2)提取图像中的特征点组成一组原始图像点vi(i＝1,…,n)，并确定与特征点对应的一组三维空间点xi(i＝1,…,n)，n为特征点的总个数；

(3)将三维空间点重投影到图像上，得到估算图像点

(4)利用摄像机内参数矩阵分别对原始图像点、估算图像点作归一化处理，并根据处理后的原始图像点、估算图像点，利用l∞范数定义三维空间点的重投影误差，构成二阶锥规划模型；

(5)将二阶锥规划模型中的圆锥约束松驰为方锥约束，将二阶锥规划问题松弛为线性规划问题；

(6)将摄像机姿态中的旋转矩阵以轴角坐标表示，使用分支定界法在旋转空间中进行搜索，并求解对应的线性规划问题，直至找到最优解。

步骤(1)中，被测摄像机的内参数矩阵k是通过文献z.zhang.flexiblecameracalibrationbyviewingaplanefromunknownorientations[c].proceedingsofthe5^thinternationalconferenceoncomputervision,1999,pp.666-673所述的单摄像机标定方法测量得到的。

步骤(2)中，根据图像中的特征点，在三维空间内找到与特征点对应位置的三维空间点，这样建立了原始图像点与三维空间点的对应关系。

步骤(3)中，估算图像点其中，r表示摄像机相对于世界坐标系的旋转矩阵，c表示摄像机的位置。

步骤(4)中，归一化处理后的原始图像点vi＝k-¹vi，估算图像点根据vi和利用l∞范数定义三维空间点的重投影误差，则摄像机外参数标定问题就可以描述成minmax优化问题：

其中，||·||表示原始图像点和估算图像点的距离，该距离应小于阈值ε，即||vi-r(xi-c)||≤ε。||vi-r(xi-c)||≤ε符合二阶锥约束的形式，若摄像机外参数旋转矩阵已知，该问题可以用二阶锥规划求解；

利用平面坐标表示原始图像点、估算图像点，则vi＝(ui,vi,1)^τ，两点距离即重投影误差满足其中，zi和分别为vi和对应的球面点vsi和的z坐标值，β表示球面点vsi与之间的弧长，至此，二阶锥规划模型可表述为：

步骤(5)中，用l∞范数替换式(2)中的l2范数，则：

且

公式(3)中，2n个线性不等式代表了n个以摄像机为中心的方锥，即公式(2)中的n个圆锥被n个方锥替代，则二阶锥规划问题松弛为线性规划问题。

步骤(6)中，旋转矩阵用轴角表示为其中α表示旋转矩阵的角，表示旋转轴的单位矢量，这样所有的三维旋转矩阵可以由半径为π的球体内的点表示。

分支定界法可以描述为：

将球体松弛成其外切立方体并将该立方体分割成小立方块dk，对每一个小立方体，计算其中心点σ等于小立方体边长的一半，判断是否有解(c,δr)满足如下问题：

判断公式(4)是否有解，

若有，则将当前的立方体平均分成8块较小立方体，并判断分得的较小立方体中是否包含球体中的任何元素，若是，进入下一次迭代判断，若否，将该较小立方体舍弃；

若否，将当前立方体舍弃；

上述过程反复迭代，直到小立方体不能再分并且满足公式(4)，迭代终止，求解得到最优的摄像机外参数r和c。

与现有技术相比，本发明将二阶锥约束松弛为线性约束，结合分支定界法和线性规划法求取全局最优解，在保证全局最优解的同时具有更快的求解速度。

附图说明

图1是本发明基于最优化估计的摄像机外参数标定方法的流程图；

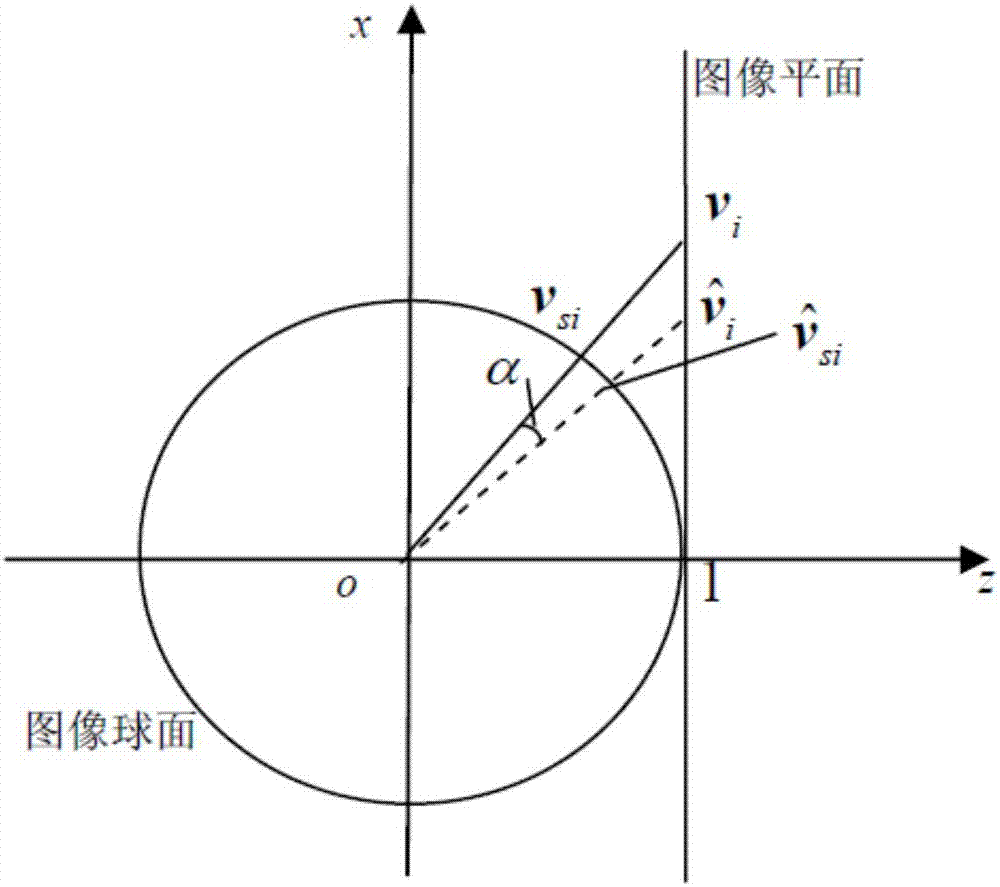
图2是本发明中图像球面和图像平面的二维图。

具体实施方式

为了更为具体地描述本发明，下面结合附图及具体实施方式对本发明的技术方案进行详细说明。

本实施例的具体实施过程如下：

s01，将被测摄像机固定，利用单摄像机标定方法确定出其内参数矩阵k，将一个空间结构已知的三维物体置于摄像机前，拍摄一幅图像。

s02，在图像中提取特征点，确定图像点与空间点的对应关系，从而得到一组空间三维点xi(i＝1,…,n)和原始图像点vi(i＝1,…,n)的对应。

s03，将三维空间点重投影到图像上，得到估算图像点

s04，利用摄像机内参数矩阵分别对原始图像点、估算图像点作归一化处理，得到处理后的原始图像点vi＝k^-1vi，估算图像点

s05，根据原始图像点vi，估算图像点用l∞范数定义三维空间点的重投影误差，摄像机外参数标定问题就可以描述成minmax优化问题：

其中，||·||表示原始图像点和估算图像点的距离，应该小于某个阈值ε，即||vi-r(xi-c)||≤ε，符合二阶锥约束的形式，若旋转矩阵已知，该问题可以用二阶锥规划求解。

本实施例采用平面坐标表示图像点，则vi＝(ui,vi,1)^τ，两点距离即重投影误差满足其中zi和分别为vi和对应的球面点vsi和的z坐标值，β表示两个球面点之间的弧长，图1为图像球面和图像平面的二维图，由于图像点坐标已经归一化，因此假设摄像机焦距为1。至此，问题求解的二阶锥规划模型可表述为：

s06，用l∞范数替换式(2)中的l2范数，于是有

且

公式(3)给出2n个线性不等式代表n个以摄像机为中心的方锥，也就是说当用l∞范数代替l2范数时，式(2)中的n个圆锥被n个方锥替代，原二阶锥规划问题松弛为线性规划问题。

s07，采用分支定界方法对旋转空间进行搜索，旋转矩阵用轴角表示为其中α表示旋转量的角，是表示旋转轴的单位矢量。这样所有的三维旋转量可以由半径为π的球体内的点表示。

为了简化算法，将球松弛成它的外切立方体把立方体分割成小的立方块，通常每次分割是将立方体平分成8块小立方体。随着立方体的尺寸逐渐变小，解就会越来越接近最优解。因此，分支定界算法可以描述为：

a.将旋转空间(球)松弛成它的外切立方体将立方体分割成小的立方体dk，对每一个小立方体，计算其中心点σ等于小立方体边长的一半，判断是否有解(c,δr)满足如下问题：

这是个可行性问题。如果不可行，那么这个小立方体就被舍弃。

b.如果(4)有解，则将这个小立方体继续平分成八块。如果分得的小立方体中不包含原旋转空间(球)中的任何元素，那么这个小立方体也被舍弃。

反复迭代步骤a和步骤b，直至小立方体包含满足要求的解，算法终止，求得最优的摄像机外参数r和c。

与hartely方法相比，本发明方法计算的r值与c值更接近真值，r值的误差在5度以内，c值的误差在2cm以内。本发明方法在保证求解精度的同时，在速度上比hartely方法有一倍以上的提升，特别适用于实时应用中。

以上所述的具体实施方式对本发明的技术方案和有益效果进行了详细说明，应理解的是以上所述仅为本发明的最优选实施例，并不用于限制本发明，凡在本发明的原则范围内所做的任何修改、补充和等同替换等，均应包含在本发明的保护范围之内。