一种用于目标跟踪的带有重要性图的特征整合方法与流程

本发明属于单目标跟踪领域，特别提出一种用于目标跟踪的带有重要性图的特征整合方法。

背景技术

单目标跟踪是计算机视觉中一项重要的任务，在实际生活中有众多应用，比如视频监控、机器人服务等。单目标跟踪的难点在于缺乏关于目标的外貌、形状的先验信息，却需要在保持跟踪速度的同时，处理各种具有挑战性的问题，比如形变、遮挡、光照。由于这些挑战的存在，目标的外貌、形状在图像序列中不断改变，因此大多数跟踪器倾向于在线更新模型，而不是学习一个固定的跟踪器。此外，缺乏训练样本也给学习一个固定的跟踪器带来了困难。

在跟踪模型中检测模型和特征表示是备受关注的两个要素。目前相关滤波是广泛使用的单目标跟踪方法，它通过循环平移进行稠密采样，近似样本在真实图像中的平移。此外避免二分类边界的二义性，相应目标使用高斯响应表示。由于卷积定理的存在，相关滤波能够在频率域快速训练和检测，同时拥有不错的精确度和鲁棒性。当然循环平移近似真实平移导致了边界效应，目前主要存在两种解决方案，一种通过裁剪获得更精确的样本，另外一种给滤波器引入二范数，惩罚力度随着到中心距离的增加而增大。提出的方法中使用裁剪的方法解决边界效应。

特征表示对于模型的效果有着至关重要的影响，主要采用手工特征或者深度特征。手工特征目前主要采用梯度方向直方图和颜色特征，但大多是简单拼接两者，并未充分发挥他们各自的优势。而深度特征牺牲了跟踪速度，获得极好的鲁棒性和精确度。提出的方法采用梯度方向直方图和灰度特征，通过重要性图发挥梯度方向直方图对光照的鲁棒性、灰度特征对形变的鲁棒性。

技术实现要素：

发明目的：本发明为了解决单目标跟踪问题，有效改进形变和光照的鲁棒性，提出了一种带有重要性图的特征整合方法。

技术实现要素：
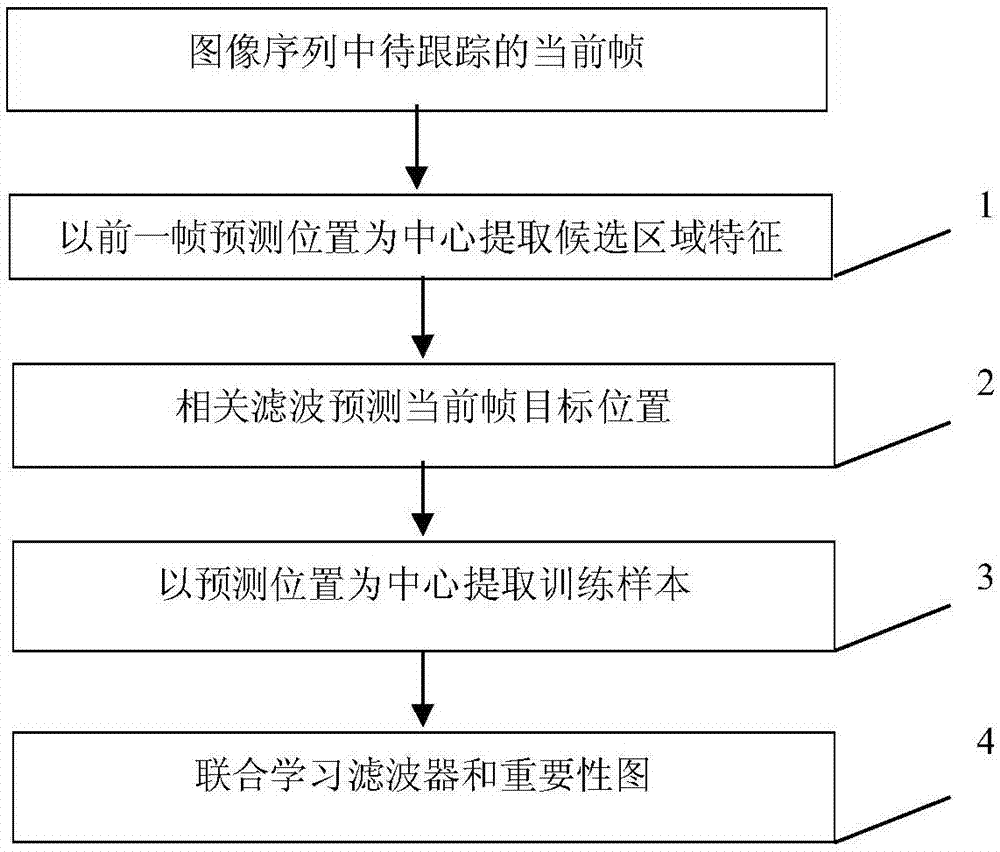
一种用于目标跟踪的带有重要性图的特征整合方法，具体包含如下步骤：

步骤1，以上一帧预测位置为中心，提取候选区域的梯度方向直方图和灰度特征；

步骤2，利用滤波器，根据最大响应值预测当前帧的目标位置；

步骤3，以当前预测目标的位置为中心，提取训练样本；

步骤4，利用相关滤波模型学习得到滤波器和重要性图，完成下一帧目标位置的预测。

作为本发明一种用于目标跟踪的带有重要性图的特征整合方法的进一步优选方案，在步骤1中，以上一帧预测位置pt-1为中心，提取候选区域特征xt∈r^dmn，其中，使用hann窗处理候选区域特征xt∈r^dmn；d指特征的维度，mn指特征中元素的个数，且xt由k个特征组成，即xt＝[x¹,x²,…,x^k]，其中，且k＝2。

作为本发明一种用于目标跟踪的带有重要性图的特征整合方法的进一步优选方案，当前帧目标位置的预测具体包括以下步骤：

步骤2.1，对特征的每个通道应用二维离散傅里叶变换，获得频率域的候选特征

步骤2.2，使用相关滤波获得响应值,根据最大响应值预测目标的位置；

其中，是上一帧训练获得的带有重要性图的滤波器；相当于将每个特征的通道对角化后拼接而成，f-¹是二维离散傅里叶变换的逆变换。

作为本发明一种用于目标跟踪的带有重要性图的特征整合方法的进一步优选方案，步骤3中，以当前帧预测位置pt为中心，提取训练样本同样的使用hann窗处理训练样本

作为本发明一种用于目标跟踪的带有重要性图的特征整合方法的进一步优选方案，利用相关滤波模型学习得到滤波器和重要性图，具体包括以下步骤：

步骤4.1，建立模型：类似于脊回归，实数域中相关滤波的目标函数以向量化的二维高斯响应y∈r^mn为目标，通过循环平移近似目标在图像中的真实平移，目标是最小化带有正则项的最小平方误差

其中，★指循环相关，xk,l指第k个特征的第l个通道，h∈r^dmn是滤波器,hk,l是对应于xk,l的滤波器，mk是第k个特征的重要性图，diag(mk)∈r^mn×mn是mk的对角化，αk是第k个重要性图的二范数系数，λ是滤波器的二范数系数；

利用卷积定理和parseval定理，将上述公式转换到频域，并且对角化；

其中，是的对角化，是带有重要性图的滤波器，f是单位离散傅里叶变换矩阵；

步骤4.2，求解模型：使用增广拉格朗日法转换问题，随后使用admm求解下列子问题；

其中，ξk,l∈r^mn是gk,l拉格朗日乘子，μ是二范数的惩罚项；

求解子问题滤波器相似于脊回归，该等式存在闭合解，但是通过利用sherman-morrison公式避开矩阵求逆操作，因此解为

其中t＝[1,2,…,mn]代表位置，

conj代表复数共轭；

求解子问题重要性图m：将关于m的目标函数转换到实数域，mk∈r^mn相互独立，因此可以分别求解

求解子问题中间变量h：将关于h的目标函数转换到实数域，hk,l∈r^mn相互独立，分别求解

更新

更新μ：其中μmax是最大值，而β是更新速率；

值得注意的是m的初始值为0矩阵，而h的初始解来自于kcf，采用bacf处理边界效应的方法，在中心处裁剪h，其余均赋值为0，更新目标特征模型后训练模型，其中是在线更新的目标特征模型，t表示帧的索引；η是学习率，通过对角化获得；

步骤4.3，直至步骤4.2达到最大迭代次数，获得滤波器和重要性图。滤波器用于下一帧的目标检测。

本发明是针对相关滤波提出的特征整合方法，与现有技术相比，本发明具有以下特征：

首先采用相关滤波框架保证跟踪的速度和精度，使用裁剪方法克服边界效应；然后，通过整合重要性图、特征整合到相关滤波框架，联合学习重要性图和滤波器；在保持速度的同时兼得特征的优势，提高跟踪器的鲁棒性，因此具有较高的使用价值。

附图说明

图1为本发明整体流程图；

图2为本发明联合学习获得滤波器和重要性图的流程图。

具体实施方式

以下结合附图说明本发明的具体实施方式。

如图1所示，本发明公开了一种用于目标跟踪的带有重要性图的特征整合方法，具体步骤如下：

步骤1，以上一帧预测位置为中心，提取候选区域的梯度方向直方图和灰度特征；

步骤2，利用滤波器，根据最大响应值预测当前帧目标的位置；

步骤3，以当前帧预测位置为中心，提取训练样本；

步骤4，联合学习滤波器和重要性图，用于下一帧目标位置的预测。

需要说明的是，本发明的核心步骤联合学习滤波器和重要性图，具体实施方式的描述主要侧重于步骤4，步骤1、2以及步骤3可采用现有技术实现。

如图2所示，联合学习获得滤波器和重要性图的具体步骤如下：

步骤4.1，建立模型。类似于脊回归，实数域中相关滤波的目标函数以向量化的二维高斯响应y∈r^mn为目标，通过循环平移近似目标在图像中的真实平移，目标是最小化带有正则项的最小平方误差

其中，★指循环相关，xk,l指第k个特征的第l个通道，h∈r^dmn是滤波器,hk,l是对应于xk,l的滤波器，mk是第k个特征的重要性图，diag(mk)∈r^mn×mn是mk的对角化，αk是第k个重要性图的二范数系数，λ是滤波器的二范数系数；

利用卷积定理和parseval定理，将上述公式转换到频域，并且对角化；

其中，是的对角化，是带有重要性图的滤波器，f是单位离散傅里叶变换矩阵；

步骤4.2，求解模型。使用增广拉格朗日法转换问题，随后使用admm求解下列子问题；

其中，ξk,l∈r^mn是gk,l拉格朗日乘子，μ是二范数的惩罚项；

求解子问题滤波器相似于脊回归，该等式存在闭合解，但是通过利用sherman-morrison公式避开矩阵求逆操作，因此解为

其中t＝[1,2,…,mn]代表位置，

conj代表复数共轭；

求解子问题重要性图m：将关于m的目标函数转换到实数域，mk∈r^mn相互独立，因此可以分别求解

求解子问题中间变量h：将关于h的目标函数转换到实数域，hk,l∈r^mn相互独立，分别求解

更新

更新μ：其中μmax是最大值，而β是更新速率；

值得注意的是m的初始值为0矩阵，而h的初始解来自于kcf，采用bacf处理边界效应的方法，在中心处裁剪h，其余均赋值为0，更新目标特征模型后训练模型，其中是在线更新的目标特征模型，t表示帧的索引；η是学习率，通过对角化获得。

步骤4.3，直至步骤4.2达到最大迭代次数，获得滤波器和重要性图。滤波器用于下一帧的目标跟踪。

以上对本发明所提供的一种用于目标跟踪的带有重要性图的特征整合方法进行了详细介绍。值得注意的是，具体实现该技术方案的方法和途径有很多，以上所述仅是本发明的优选实施方式，只用于帮助理解本发明的方法及核心思想；同时，对于本领域的一般技术人员，在本发明核心思想的基础上，做出的修改和调整都将视为本发明的保护范围。综上所述，本说明书内容不应理解为对本发明的限制，本发明的保护范围应由所附的权利要求来限定。