多晶硅还原工序能耗值的预测方法、系统、介质及设备与流程

本发明涉及生产工艺能耗预测领域，特别涉及一种多晶硅还原工序能耗值的预测方法、系统、介质及设备。

背景技术

多晶硅作为光伏转换器最好的制作材料之一，有95％的太阳能电池都是以多晶硅作为原材料，其主要的生产方法有西门子法、冶金法和碳热还原法等等。其中，西门子法是生产多晶硅最为成熟的工艺技术，该工艺流程主要包括三氯氢硅合成工艺、三氯氢硅精馏提纯工艺、三氯氢硅还原工艺和尾气回收再利用工艺。而三氯氢硅还原工艺是多晶硅生产的核心技术，长期被国外企业所垄断，我国工艺技术水平落后，每生产1kg的多晶硅将消耗10～15kg的三氯氢硅，能量消耗巨大，而利用预测模型可以对多晶硅还原工序的能耗值进行预测，从而工作人员可以根据多晶硅还原工序的能耗值对多晶硅还原工序的生产流程进行控制，进而达到提高多晶硅生产效率的目的，该方法在目前市场上应用较为广泛。但是，在现有技术当中，大多数的预测模型对多晶硅还原工序能耗值进行预测时，都存在预测精度较低的问题，由此可见，如何利用一种更好的方法来提高多晶硅还原工序能耗值的预测精度，是本领域技术人员亟待解决的问题。

技术实现要素：

有鉴于此，本发明的目的在于提供一种多晶硅还原工序能耗值的预测方法、系统、介质及设备，以提高多晶硅还原工序能耗值的预测精度。其具体方案如下：

一种多晶硅还原工序能耗值的预测方法，包括：

获取多晶硅还原工序能耗值的影响因素；

利用小波神经网络算法对所述影响因素进行建模，得到初始化模型；

利用sfla算法对所述初始化模型进行优化，得到目标模型；

利用所述目标模型对目标多晶硅还原工序的能耗值进行预测。

优选的，所述利用小波神经网络算法对所述影响因素进行建模，得到初始化模型的过程之前，还包括：

对所述影响因素进行降维处理。

优选的，所述对所述影响因素进行降维处理的过程，包括：

利用pca算法对所述影响因素进行降维处理。

优选的，所述小波神经网络算法的模型表达式为：

式中，n为隐层节点的个数，wij为连接隐含层节点i和输入层结点j的权值，φx,y为连续小波，x为小波神经网络算法中当前隐含节点的伸缩系数，y为小波神经网络算法中当前隐含节点的平移系数，p为输入层结点的个数，wjk为连接隐含层节点j和输入层结点k的权值。

优选的，所述利用sfla算法对所述初始化模型进行优化，得到目标模型的过程之后，还包括：

利用测试数据检测所述目标模型的预测精度。

优选的，所述利用sfla算法对所述初始化模型进行优化，得到目标模型的过程，包括：

利用sfla算法建立初始化参数，以确定蛙群中青蛙的数量f和族群的数量m，并计算所述蛙群中每一只青蛙的适应值；

将所有青蛙按照适应值的大小进行降序排列，并将排序后的f只青蛙按照预设分配条件分配至m个族群当中；

利用文化基因算法对每一个族群中的青蛙作优化，得到优化青蛙；

将所述m个族群中的优化青蛙进行混合，以确定出所述蛙群中的最优解；

判断所述最优解是否满足预设筛选条件；

若是，则将所述最优解输入至所述初始化模型，以得到所述目标模型。

优选的，所述判断所述最优解是否满足预设筛选条件的过程之后，还包括：

若否，则再次执行将所有青蛙按照适应值的大小进行降序排列，并将排序后的f只青蛙按照预设分配条件将所述f只青蛙分配至m个族群当中的步骤。

相应的，本发明还公开了一种多晶硅还原工序能耗值的预测系统，包括：

因素获取模块，用于获取多晶硅还原工序能耗值的影响因素；

模型初始化模块，用于利用小波神经网络算法对所述影响因素进行建模，得到初始化模型；

模型优化模块，用于利用sfla算法对所述初始化模型进行优化，得到目标模型；

模型预测模块，用于利用所述目标模型对目标多晶硅还原工序的能耗值进行预测。

相应的，本发明还公开了一种计算机可读存储介质，所述计算机可读存储介质上存储有计算机程序，所述计算机程序被处理器执行时实现如前述公开的多晶硅还原工序能耗值的预测方法的步骤。

相应的，本发明还公开了一种多晶硅还原工序能耗值的预测设备，包括：

存储器，用于存储计算机程序；

处理器，用于执行所述计算机程序时实现前述公开的多晶硅还原工序能耗值的预测方法的步骤。

可见，在本发明中，首先是获取影响多晶硅还原工序能耗值的影响因素，然后，利用小波神经网络算法对影响因素进行建模，得到初始化模型，显然，由于小波神经网络算法具有自学习功能，那么，就可以利用小波神经网络算法对影响多晶硅还原工序更多的影响因素进行分析，因此，利用小波神经网络算法创建的初始化模型对目标多晶硅还原工序能耗值进行预测时，就能够显著提高目标多晶硅还原工序能耗值的预测精度。并且，在得到初始化模型之后，又再次利用sfla算法对初始化模型进行优化，得到目标模型，以避免初始化模型中的参数陷入局部最优解，所以，利用该种方法可以进一步提高目标模型的预测精度，显然，利用本发明中的目标模型对目标多晶硅还原工序能耗值进行预测时，就会进一步提高目标多晶硅还原工序能耗值的预测精度。相应的，本发明公开的一种多晶硅还原工序能耗值的预测系统、介质及设备，同样具有上述有益效果。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据提供的附图获得其他的附图。

图1为本发明实施例提供的一种多晶硅还原工序能耗值的预测方法的流程图；

图2为本发明实施例提供的另一种多晶硅还原工序能耗值的预测方法的流程图；

图3为本发明实施例提供的一种多晶硅还原工序能耗值的预测系统的结构图；

图4为本发明实施例提供的一种多晶硅还原工序能耗值的预测设备的结构图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

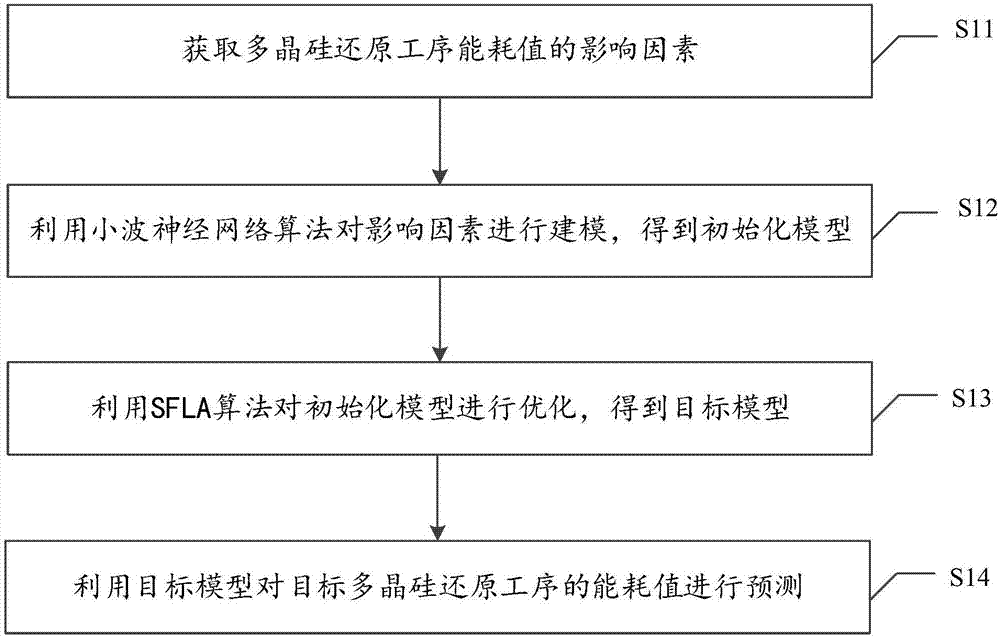
本发明实施例公开了一种多晶硅还原工序能耗值的预测方法，如图1所示，该方法包括：

步骤s11：获取多晶硅还原工序能耗值的影响因素；

在本实施例中，为了对多晶硅还原工序的能耗值进行预测，首先，需要获取影响多晶硅还原工序的影响因素，比如：还原炉的结构、还原炉中硅棒的布置方式、还原炉内沉积物的温度、还原炉内的压力、还原炉内三氯氢硅和氢气的配比、硅棒的电流和电压等等。当然，在实际应用当中，还有很多其它能够影响多晶硅还原工序的影响因素，此处不再进行一一列举。

步骤s12：利用小波神经网络算法对影响因素进行建模，得到初始化模型；

步骤s13：利用sfla算法对初始化模型进行优化，得到目标模型；

可以理解的是，因为小波神经网络算法结构简单、收敛速度快，具有强大的自学习能力，并且，能够通过小波神经网络算法中的尺度伸缩因子和平移因子对输入数据进行多尺度分析，提取到更多输入数据中的有效信息，所以，在本实施例中，是利用小波神经网络算法来对影响因素进行建模，得到能够对目标多晶硅还原工序能耗值进行预测的初始化模型。

此外，由于利用小波神经网络算法创建的初始化模型当中有一些参数是比较固定的，容易使得创建的初始化模型陷入局部最优解，在此种情况下，初始化模型并不能对目标多晶硅还原工序的能耗值进行最佳的预测，所以，在本实施例中，还利用sfla算法(蛙跳算法)对基于小波神经网络算法创建的初始化模型进行优化，以避免初始化模型中的参数陷入局部最优解，然后得到目标模型。

步骤s14：利用目标模型对目标多晶硅还原工序的能耗值进行预测。

能够想到的是，当利用sfla算法对初始化模型进行优化，寻找到初始化模型中的最优参数，得到目标模型之后，就可以利用目标模型来对目标多晶硅还原工序的能耗值进行预测，得到目标多晶硅还原工序的能耗值。显然，当得到目标多晶硅还原工序的能耗预测值之后，就能够根据预测得到的目标多晶硅的能耗预测值对目标多晶硅的还原工序进行调整和改良，以提高目标多晶硅的生产效率。

需要说明的是，此处的目标多晶硅是指待预测还原工序能耗值的多晶硅，上述步骤过程中提及到的多晶硅是指创建初始化模型时所用到的影响多晶硅还原工序的数据样本。并且，本实施例提供的一种多晶硅还原工序能耗值的预测方法，还可以应用于其它与多晶硅还原工序相类似的工艺流程，比如：铁还原工序和铜还原工序的能耗值预测等等。

可见，在本实施例中，首先是获取影响多晶硅还原工序能耗值的影响因素，然后，利用小波神经网络算法对影响因素进行建模，得到初始化模型，显然，由于小波神经网络算法具有自学习功能，那么，就可以利用小波神经网络算法对影响多晶硅还原工序更多的影响因素进行分析，因此，利用小波神经网络算法创建的初始化模型对目标多晶硅还原工序能耗值进行预测时，就能够显著提高目标多晶硅还原工序能耗值的预测精度。并且，在得到初始化模型之后，又再次利用sfla算法对初始化模型进行优化，得到目标模型，以避免初始化模型中的参数陷入局部最优解，所以，利用该种方法可以进一步提高目标模型的预测精度，显然，利用本实施例中的目标模型对目标多晶硅还原工序能耗值进行预测时，就会进一步提高目标多晶硅还原工序能耗值的预测精度。

基于上述实施例，本实施例对上述实施例作进一步的说明与优化，具体的，上述步骤s12：利用小波神经网络算法对影响因素进行建模，得到初始化模型的过程之前，还包括：

对影响因素进行降维处理。

可以理解的是，影响多晶硅还原工序能耗值的影响因素多种多样，在这些影响因素当中，必然会有一些影响因素呈现出线性相关的特性，所以，在本实施例中，为了减少在后续流程步骤中对数据进行处理时的数据处理数量，还对获取到的影响多晶硅还原工序的影响因素进行了降维处理，以进一步提高创建初始化模型的速度。

具体的，上述步骤：对影响因素进行降维处理的过程，包括：

利用pca算法对影响因素进行降维处理。

具体的，在本实施例中，是利用pca算法(principalcomponentanalysis)来对影响多晶硅还原工序能耗值的影响因素进行降维处理，也即，利用pca算法去除掉影响多晶硅还原工序能耗值的影响因素中互不相关的特征量，从而达到减少影响多晶硅还原工序影响因素的目的，进而可以极大的减少在后续流程步骤中对数据进行处理时的数据处理数量。

当然，在实际操作当中，还可以利用lda算法(lineardiscriminantanalysis，线性判别法)、kpca(kernelprincipalcomponentanalysis，基于核的主成分分析算法)来对影响多晶硅还原工序的影响因素进行降维处理，此处不作具体的限定。

基于上述实施例，本实施例对上述实施例作进一步的说明与优化，具体的，小波神经网络算法的模型表达式为：

式中，n为隐层节点的个数，wij为连接隐含层节点i和输入层结点j的权值，φx,y为连续小波，x为小波神经网络算法中当前隐含节点的伸缩系数，y为小波神经网络算法中当前隐含节点的平移系数，p为输入层结点的个数，wjk为连接隐含层节点j和输入层结点k的权值。

在本实施例中，是提供了小波神经网络算法的数学模型表达式，通过该数学模型表达式就可以对影响多晶硅还原工序能耗值的影响因素进行建模，得到初始化模型。

并且，需要说明的是，在小波神经网络算法中，是利用梯度下降法来对网络模型中待确定的参数，比如：输出层权值wij、隐含层权值wjk、伸缩因子xj、平移因子yj进行求解，计算得到小波神经网络算法中的梯度值。能够想到的是，利用该种方法就能够提取到更多影响多晶硅还原工序的影响因素。

其中，小波神经网络算法中目标函数的数学表达式为：

式中，为k个输入样本的第i个输出节点的实际输出值，为与对应的小波神经网络的预测输出值，k为输入样本的总数，n为输出空间的维度数。

小波神经网络算法中输入层的权重为：

式中，为k个输入样本的第个输出节点的实际输出值，为与对应的小波神经网络的预测输出值，k为输入样本的总数，φx,y为连续小波，x为小波神经网络算法中当前隐含节点的伸缩系数，y为小波神经网络算法中当前隐含节点的平移系数；

小波神经网络算法中输出层的权重为：

式中，为k个输入样本的第i个输出节点的实际输出值，为与对应的小波神经网络的预测输出值，k为输入样本的总数，φx,y为连续小波，x为小波神经网络算法中当前隐含节点的伸缩系数，y为小波神经网络算法中当前隐含节点的平移系数，xj为伸缩因子。

以上为小波神经网络算法中一些关键参数模型及函数的数学模型表达式，显然，基于小波神经网络算法理论，通过上述模型表达式就可以对多晶硅还原工序能耗值的影响因素进行建模，得到初始化模型。

基于上述实施例，本实施例对上述实施例作进一步的说明与优化，具体的，上述步骤s13：利用sfla算法对初始化模型进行优化，得到目标模型的过程之后，还包括：

利用测试数据检测目标模型的预测精度。

为了进一步检测目标模型对多晶硅还原工序能耗值的预测精度，在本实施例中，还利用测试数据对目标模型的预测精度进行了检测。具体的，在实际操作当中，可以是在获取多晶硅还原工序能耗值的影响因素时，将这些影响因素划分为训练数据和测试数据，然后，利用训练数据对初始化模型进行训练，之后，再利用测试数据对目标模型的预测精度进行检验，以此来判断目标模型的精确程度。显然，通过此种方法，工作人员就可以及时知晓目标模型的预测精度，并以此来对目标多晶硅还原工序的生产流程进行调控。

基于上述实施例，本实施例对上述实施例作进一步的说明与优化，如图2所示，具体的，上述步骤s13：利用sfla算法对初始化模型进行优化，得到目标模型的过程，包括：

步骤s131：利用sfla算法建立初始化参数，以确定蛙群中青蛙的数量f和族群的数量m，并计算蛙群中每一只青蛙的适应值；

步骤s132：将所有青蛙按照适应值的大小进行降序排列，并将排序后的f只青蛙按照预设分配条件分配至m个族群当中；

在本实施例中，将具体阐述一下如何利用sfla算法对初始化模型进行优化，得到目标模型。sfla算法的主要原理是：假设在一片湿地当中生活着一群青蛙，青蛙通过不同的石头进行跳跃寻找食物较多的地方。每只青蛙通过文化交流实现信息的互换，而每只青蛙可以被定义为问题的一个解，然后，将整个青蛙群体被分为不同的族群，每个族群也会有自己的文化，也即，青蛙通过在族群中跳跃，执行局部搜索策略，寻找局部最优解。此外，族群中的每只青蛙都会有自己的文化，并且，这些青蛙的文化会随着子群体的进化而进化，当子群体进化到一定阶段之后，各个子群体之间再进行信息的交换，以实现子群体之间的混合运算，一直到满足预设条件为止，就寻找到了全局最优解。

也即，首先是利用sfla算法建立初始化参数，以确定蛙群中青蛙的数量f和族群的数量m，并计算蛙群中每一只青蛙的适应值。当计算得到了蛙群中每一只青蛙的适应值之后，就可以将所有青蛙按照适应值的大小进行降序排列，并将排序后的f只青蛙按照预设分配条件分配至m个族群当中。

此处的预设分配条件通过一个具体的例子来进行说明，假设蛙群中青蛙的数量为9只，族群的数量为3，那么当这9只青蛙按照适应值的大小进行降序排列之后，就可以将排在第一位的青蛙放置到第一个族群当中，将排在第二位的青蛙放置在第二个族群当中，将排在第三位的青蛙放置在第三个族群当中，之后，将排在第四位的青蛙放置在第一个族群当中，将排在第五位的青蛙放置在第二个族群当中，将排在第六位的青蛙放置在第三个族群当中，以此类推，直至将这9只青蛙放置在3个族群当中。

步骤s133：利用文化基因算法对每一个族群中的青蛙作优化，得到优化青蛙；

步骤s134：将m个族群中的优化青蛙进行混合，以确定出蛙群中的最优解；

步骤s135：判断最优解是否满足预设筛选条件；

步骤s136：若是，则将最优解输入至初始化模型，以得到目标模型。

当将f只青蛙放置到m个族群当中时，就可以利用文化基因算法对每一个族群当中的青蛙进行优化，得到优化青蛙，显然，此操作的目的是为了使得每一只青蛙更加接近族群当中的最优值，之后，将m个族群当中的优化青蛙进行混合，也即，当每一个族群当中的青蛙都执行了文化基因算法的进化之后，让每一只青蛙在各个族群当中进行跳跃，以对各个族群当中的青蛙进行重新组合，重新合并得到一个新蛙群，然后，重新计算新蛙群中每一个青蛙的适应值，并按照适应值的大小重新对新蛙群中的青蛙进行降序排列，以确定出新蛙群中具有最优适应值的青蛙，也即，确定出新蛙群中的最优解，当确定出新蛙群中的最优解时，判断该最优解是否满足预设筛选条件，也即，判断该最优解是否达到迭代终止条件，若达到迭代终止条件，则停止对最优解的寻优迭代，并将最优解输入至初始化模型当中，以得到目标模型。

相应的，上述步骤s135：判断最优解是否满足预设筛选条件的过程之后，还包括：

若否，则再次执行将所有青蛙按照适应值的大小进行降序排列，并将排序后的f只青蛙按照预设分配条件将f只青蛙分配至m个族群当中的步骤。

可以理解的是，如果搜索得到的最优解并不满足预设筛选条件，则说明该最优解并不是蛙群中的全局最优解，此时需要再次返回执行步骤s132，以重新确定出蛙群中的最优值，从而达到对初始化模型中的参数进行优化目的，以得到目标模型。

相应的，本发明还公开了一种多晶硅还原工序能耗值的预测系统，如图3所示，该系统包括：

因素获取模块21，用于获取多晶硅还原工序能耗值的影响因素；

模型初始化模块22，用于利用小波神经网络算法对影响因素进行建模，得到初始化模型；

模型优化模块23，用于利用sfla算法对初始化模型进行优化，得到目标模型；

模型预测模块24，用于利用目标模型对目标多晶硅还原工序的能耗值进行预测。

相应的，本发明还公开了一种计算机可读存储介质，计算机可读存储介质上存储有计算机程序，所述计算机程序被处理器执行时实现如前述公开的多晶硅还原工序能耗值的预测方法的步骤。

相应的，本发明还公开了一种多晶硅还原工序的能耗预测设备，如图4所示，该设备包括：

存储器31，用于存储计算机程序；

处理器32，用于执行计算机程序时实现如前述公开的多晶硅还原工序能耗值的预测方法的步骤。

本说明书中各个实施例采用递进的方式描述，每个实施例重点说明的都是与其它实施例的不同之处，各个实施例之间相同或相似部分互相参见即可。对于实施例公开的装置而言，由于其与实施例公开的方法相对应，所以描述的比较简单，相关之处参见方法部分说明即可。

最后，还需要说明的是，在本文中，诸如第一和第二等之类的关系术语仅仅用来将一个实体或者操作与另一个实体或操作区分开来，而不一定要求或者暗示这些实体或操作之间存在任何这种实际的关系或者顺序。而且，术语“包括”、“包含”或者其任何其他变体意在涵盖非排他性的包含，从而使得包括一系列要素的过程、方法、物品或者设备不仅包括那些要素，而且还包括没有明确列出的其他要素，或者是还包括为这种过程、方法、物品或者设备所固有的要素。在没有更多限制的情况下，由语句“包括一个……”限定的要素，并不排除在包括所述要素的过程、方法、物品或者设备中还存在另外的相同要素。

以上对本发明所提供的一种多晶硅还原工序能耗值的预测方法、系统、介质及设备进行了详细介绍，本文中应用了具体个例对本发明的原理及实施方式进行了阐述，以上实施例的说明只是用于帮助理解本发明的方法及其核心思想；同时，对于本领域的一般技术人员，依据本发明的思想，在具体实施方式及应用范围上均会有改变之处，综上所述，本说明书内容不应理解为对本发明的限制。