基于飞行数据分析的飞机离场燃油消耗评估方法与流程

本发明属于机场绿色交通技术，尤其涉及一种侧风影响下机场终端区离场燃油消耗评估方法。

背景技术：

空中交通持续和快速增长，据预测在下一个15年，空中交通量将翻倍。同时，燃油价格的上涨和环境政策限制的矛盾，降低飞机的燃油消耗问题成为空管和签派的管理者和研究者关注的热点问题。据2017年IATA报道，飞机的燃油消耗在航空公司所占比重最大的运营成本支出。准确评估飞机的燃油消耗可以最大限度地减少燃油排放对环境的有害影响，可以节约燃油能源，降低飞行成本，实现更精确的飞行轨迹预测，并实现有效的空中交通管理。因此，航空公司纷纷将降低燃油消耗的目光集中于精确估计飞机燃油加载量，避免“油烧油”的现象。终端空域是空中交通的枢纽，燃油排放的限制和快速增长的交通量矛盾尤为突出。在终端区飞机飞行活动中，相对于进场和场面滑行阶段，离场起飞的燃油消耗较大。因此，建立符合运行实际的离场燃油消耗评估模型，精确控制燃油加载量，对于提高航空公司运营效益，降低终端区燃油排放具有重要意义。

飞机运行中燃油消耗量受到诸多性能指标的影响，主要影响因素包括飞机质量、速度，大气密度、温度、压力、以及侧风等气象环境。由此可见，现有技术中，首先，各燃油消耗预测方法中均存在不足，其中基于能量守恒原理进行建模未考虑爬升阶段水平面因素，且未考虑侧风这种气象因素；基于神经网络训练模型进行预测使得结果抖动明显，油耗总量估计结果与真实值存在一定误差，并且未分析飞机性能参数对燃油消耗的影响；采用线性回归方法对真实数据的要求很大，且目前文献不涉及气象因素及性能参数从而导致预测精度降低。其次，现阶段爬升阶段燃油消耗研究大多数涉及在常规爬升阶段燃油消耗的影响，极少考虑连续爬升阶段对其影响，且未涉及两者之间比较。最后，实际的气动参数非定值，文献中将其设为定值会导致计算结果存在误差。

飞机燃油消耗的准确评估是航空公司降低飞行成本和控制燃油排放的重要手段。相当多的文献都提出了燃油消耗评估模型，目的是建立更接近于燃油消耗真实值的研究方法。一些政府组织先后建立了飞机燃油消耗和排放的计算工具和计算方法，如ICAO，FAA 和欧控。FAA建立了AEDT，用于预测商业飞机的燃油消耗和排放。欧控采用BADA数据库计算飞行全过程阶段的燃油消耗量和排放量。此外，一些学者提出了诸多燃油消耗的评估方法，如影响燃油消耗的诸多主要因素分析，基于性能数据的燃油消耗分析，采用能量守恒原理，神经网络和回归分析等预测燃油消耗量，以及不同飞行航迹下的燃油消耗差异分析等。此外，离场连续爬升模式与传统离场爬升模式相比，具有节约燃油，提高旅客舒适性，缓解机场噪声、减少废气排放以及减少管制人员与机组人员工作量等优点，相关研究者围绕离场连续爬升运行模式下飞机的燃油成本和飞行安全性等进行了研究，例如，验证终端区内连续爬升运行模式(CCO)的最佳飞行剖面和燃油成本最小化问题，连续爬升运行模式的轨迹优化和运行效率，将连续爬升运行模式与传统爬升运行模式燃油消耗状况进行了对比分析，但提出的这些燃油消耗模型时未考虑侧风对燃油消耗的影响，以及采用理想数据拟合气动参数之间的关系，导致计算结果不准确。可见，现有技术中，燃油消耗模型中气动参数需要查阅由风洞试验获取的静态图表关系，但无法估计由于飞机性能衰减造成的额外耗油，同时较少涉及侧风对燃油消耗的影响，导致计算结果不准确。

技术实现要素：

为解决上述问题，本发明提出一种基于飞行数据分析的飞机离场燃油消耗评估方法，在QAR实际飞行数据的基础上，采用真实数据的函数拟合方法得到气动参数之间的函数关系，并结合建立的侧风动力学模型，修正BADA数据库中爬升阶段的飞机燃油消耗模型(本文简称BADA爬升阶段燃油消耗模型)，以实现燃油加载量的精确控制，避免飞行前所加油量过多从而导致“油烧油”现象的发生，从而减少燃油成本。

基于飞行数据分析的飞机离场燃油消耗评估方法，包括：

获取待分析机型的多组QAR实际飞行数据，从中提取不同马赫数条件下所对应的多组阻力系数与升力系数数据；

根据所提取的数据拟合出不同马赫数对应的趋势曲线，初步确定至少一个符合所述趋势曲线的函数，并根据所述函数得到阻力系数与升力系数之间的拟合关系；结合拟合优度和残差平方和确定所述拟合关系中的最优拟合结果；

基于BADA爬升阶段燃油消耗模型求出升力系数，再由所述最优拟合关系得到近似阻力系数；

考虑三维风对飞行地速的影响，建立加入侧风后的阻力和推力计算公式；

根据所述计算公式修正BADA爬升阶段燃油消耗模型，得到改进的BADA爬升阶段燃油消耗模型；

将所述升力系数和近似阻力系数代入改进的BADA爬升阶段燃油消耗模型，得到待分析机型在离场爬升阶段的燃油消耗量。

进一步的，所述BADA爬升阶段燃油消耗模型包括：

涡轮喷气式发动机飞机单位时间内单位推力的燃油消耗量η为：

结合标称飞行剖面中飞机爬升阶段的推力得到单位时间的燃油消耗量fclimb为：

fclimb＝ηT (2)

飞机在飞行中受到的升力L、阻力D及推力T计算公式为：

整个爬升阶段的燃油消耗量计算公式为：

其中，海拔高度与大气温度、压力及密度的关系式如下：

T1＝T0-1.98×(H/1000) (7)

pa＝p0(1-0.02257H)^5.256 (8)

根据计算式(7)、(8)和(9)计算出各个海拔高度对应的大气温度、压力及密度；

建立加入侧风后的阻力和推力计算公式，具体包括：

根据飞机爬升受到的风速大小Vwind和风速方向Dwind计算风速在地面坐标系中的投影矢量[uwg vwg wwg]^T，即：

wwg＝0 (12)

有侧风时，飞机的地速在[u v w]^T机体坐标系中的投影矢量VGS为：

式中，Lbk，Lbg分别为：

[uwg vwg wwg]^T由式(10)、(11)和(12)计算得到，即飞机的地速为：

由式(3)和(4)得到加入侧风后的阻力与推力计算公式如下：

根据式(16)和(17)修正式(1)、(2)和(6)，得到改进的BADA爬升阶段燃油消耗模型如下：

上述公式中，Cf1、Cf2表示燃油消耗系数，由BADA数据库中.OPF格式文件提供；F表示总燃油消耗量；S表示飞机机翼面积；N表示发动机台数；k表示时间点数；VTAS表示飞机的真空速；VGS表示飞行地速；Vk表示飞机的航迹速度；γ表示飞机的航迹角；m表示飞机的质量；g表示飞机的重力加速度；CL表示升力系数；CD表示阻力系数；H表示海拔高度；pa表示海拔高度为H的大气压力；p0表示海拔高度为0km时的大气压力；ρ表示海拔高度为H的大气密度；T0为设定的温度常量；T1表示海拔高度为H对应的大气温度；Lbk表示航迹坐标系到机体坐标系的坐标转换矩阵；Lbg表示地面坐标系到机体坐标系的坐标转换矩阵；表示飞机爬升阶段的偏航角；φ表示飞机爬升阶段的滚转角；θ表示飞机爬升阶段的俯仰角。

进一步的，所述风速方向以真经线正北方向为0°，顺时针为正。

进一步的，所述风速大小和风速方向通过查询不同地区不同高度的气象数据获取。

进一步的，所述T0为20摄氏度。

进一步的，所述函数包括幂函数、指数函数和多项式函数。

进一步的，所述最优拟合结果的拟合优度值最接近1，残差平方和值最小。

本发明具有以下有益效果：

1)针对气动参数往往需要查阅由风洞试验方法获取的静态图表关系，无法估计由于飞机性能衰减造成的额外耗油，从而导致燃油计算结果与实际耗油存在误差，本发明对BADA爬升阶段燃油消耗模型中升力系数和阻力系数之间的关系采用了基于QAR数据拟合的方法获得，确定了无风条件下的燃油消耗优化模型。

2)针对以往燃油消耗模型研究中较少涉及侧风对燃油消耗的影响，导致计算结果不准确问题，本发明通过对离场爬升阶段的飞行动力学分析，在燃油消耗优化模型中加入了侧风参数，保证了燃油消耗计算的准确性。

3)引入QAR实际运行参数，对比分析传统爬升运行模式和连续爬升运行模式的燃油消耗量，得到采用离场连续爬升离场比采用传统离场爬升离场要节省燃油，并分析了 飞机质量和爬升角度不同情况下对于燃油消耗的影响，验证模型的同时，体现飞机质量和爬升角度对燃油消耗影响的重要性以及是如何影响的。

4)本方法尤其适用于机场终端区离场飞行程序设计和飞行计划编排，以保证空中交通运行的安全高效。

附图说明

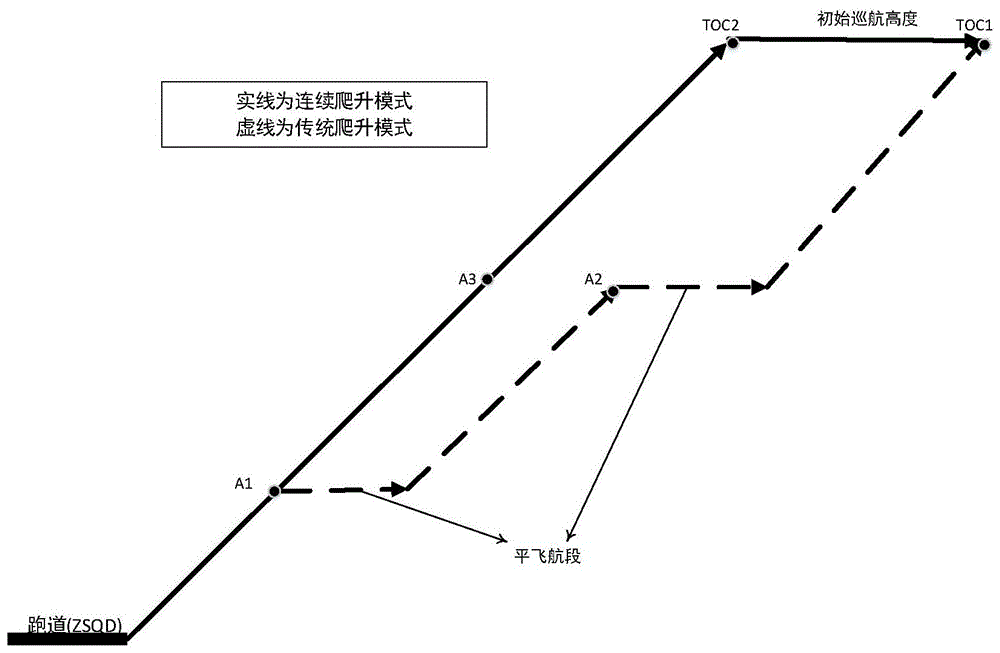
图1为飞行剖面对比图；

图2为QAR真实轨迹与仿真轨迹对比图；

图3为空客A320极特性曲线；

图4为幂函数拟合图；

图5为指数函数拟合对比图；

图6为多项式函数拟合对比图，其中，图6(a)为一次函数与二次函数对比图，图6(b)为一次函数与三次函数对比图；

图7为空客A320三维关系图；

图8为燃油消耗对比图；

图9为各个飞行阶段QAR燃油消耗量分别与风洞实验计算燃油消耗量差值、气动参数拟合计算燃油消耗量差值比较图；

图10为燃油消耗对比图2；

图11为山西太原武宿国际机场离场燃油消耗对比图；

图12为两种离场爬升模式燃油消耗对比图；

图13为不同飞行质量燃油消耗对比图；

图14为不同爬升角燃油消耗对比图；

图15为空客A321三维关系图；

图16为空客A320与空客A321燃油消耗对比图。

具体实施方式

当今全球航油价格持续上涨，燃油成本在民航运输成本中所占比例居高不下，严重影响到航空公司生存和发展。飞机燃油消耗的准确评估是航空公司降低飞行成本和控制燃油排放的重要手段。目前传统的燃油消耗模型中气动参数需要查阅由风洞试验获取的静态图表关系，但无法估计由于飞机性能衰减造成的额外耗油，同时较少涉及侧风对燃 油消耗的影响，导致计算结果不准确。为解决上述问题，本发明通过建立基于BADA数据库的飞机离场燃油消耗评估模型，可以精确控制燃油加载量。

BADA飞机性能数据库模型是由欧洲航空安全组织开发的分析飞行动力学的模型，主要应用于飞行仿真、航迹预测、排放评估及油耗计算等方面，且在飞行仿真度、复杂度和精确度上具有很大优势。

BADA数据库中飞机爬升阶段燃油消耗模型所涉及到的主要参数意义说明如下：

η 单位时间内单位推力的燃油消耗量，kg/(min·kN)；

VTAS 飞机的真空速，knots；

Cf1,Cf2 飞机在爬升阶段的燃油消耗系数；

fclimb 单位时间的燃油消耗量，kg/min；

T 飞机在爬升阶段的推力，kN；

D 飞机在爬升阶段的阻力，kN；

L 飞机在爬升阶段的升力，kN；

m 飞机的质量,kg；

g 飞机的重力加速度，kg/s²；

γ 飞机的航迹角；

VTAS 飞行真空速,knots；

VGS 飞行地速,knots；

CL 升力系数；

CD 阻力系数；

S 飞机机翼面积,m²。

F 总燃油消耗量，

N 发动机台数；

k 时间点数；

T1 海拔高度为H对应的大气温度，T0取20℃；

pa 海拔高度为H的大气压力,Pa；

p0 海拔高度为0km时的大气压力，取p0＝0.1013MPa；

H 海拔高度，Metres；

ρ 海拔高度为H时的大气密度，kg/m³。

Vwind 飞机爬升受到的风速大小，knots；

Dwind 飞机爬升受到的风速方向；

Lbk 航迹坐标系到机体坐标系的坐标转换矩阵；

Vk 飞机的航迹速度；

Lbg 地面坐标系到机体坐标系的坐标转换矩阵；

飞机爬升阶段的偏航角；

φ 飞机爬升阶段的滚转角；

θ 飞机爬升阶段的俯仰角；

BADA数据库中爬升阶段的飞机燃油消耗模型表述如下：

涡轮喷气式发动机飞机单位时间内单位推力的燃油消耗量为：

结合标称飞行剖面中飞机爬升阶段的推力便可推出单位时间的燃油消耗量为：

fclimb＝ηT (2)

上述公式中的燃油消耗系数Cf1，Cf2可由BADA数据库中.OPF格式文件提供，以A320机型为例，其性能参数值：Cf1＝0.63330，Cf2＝859.03。

飞机在飞行中会受到升力、重力、阻力及推力作用，直接影响其飞行速度，根据爬升阶段受力分析及气动参数性能数据可计算阻力及推力模型表示如下：

通过以上两组模型，根据阻力可得到推力；根据推力可获取爬升阶段飞行过程中各时刻的燃油消耗量，通过叠加可得出整个爬升阶段的燃油消耗量，公式为：

大气是包围地球的一层气体混合物，其主要参数为压强、温度、密度，这些参数值在垂直方向上变化较大而在水平面上较均匀，随着高度升高，气温降低、空气密度变小， 空气易被压缩，改善了热能的利用，燃油消耗率减小。海拔高度与大气温度、压力及密度的关系式：

T1＝T0-1.98×(H/1000) (7)

pa＝p0(1-0.02257H)^5.256 (8)

根据计算式(7)、(8)和(9)，即可计算出各个海拔高度对应的大气温度、压力及密度。

本发明对上述基于BADA数据库的爬升阶段燃油消耗模型做如下两方面进行优化，包括气动参数和侧风影响。

一、气动参数的优化

基于QAR实际运行数据，本发明采用真实数据的函数拟合方法，得出阻力系数与升力系数的关系表达式。

以A320机型为例。首先获取某航空公司A320机型多组QAR数据，将数据提取出不同马赫数条件下所对应的多组阻力系数与升力系数数据，如表1所示。

表1 A320飞机的QAR数据

将表1中马赫数为0.7的数据导入数据分析软件中，拟合出该数据的图像曲线，根据图像中数据的趋势曲线，确定符合该趋势曲线的函数。常见的拟合函数有幂函数、指数函数和多项式函数，其中：幂函数的标准形式为y＝a×x^κ，κ是大于1的有理数，a为系数；指数函数的标准形式为y＝b×c^x，c是大于1的常数，b为系数；多项式函数的标准形式为y＝anxⁿ+an-1x^n-1+…+a1x+a0，其中a0,a1,…,an均为各项的系数，n为该多项式中最高次数。

通过拟合优度(R²)及残差平方和(SSE)来确定幂函数、指数函数以及多项式函数最优拟合结果。R²的值越接近1，说明其对观测值的拟合程度越好；残差平方和是用以反映变量之间相关关系密切程度的统计指标，其值越小，拟合结果越精确。其他马赫数所 对应的拟合关系按照同样的方法获得。基于前面通过式(5)可求出的升力系数，再由拟合出的阻力系数与升力系数关系得出准确的近似阻力系数。

二、侧风下的燃油消耗计算

飞行环境特别是侧风，对燃油消耗有着较大影响，而飞机受侧风影响又随着地理位置、飞行高度H而变化。现有技术中的很多燃油消耗模型未考虑侧风对燃油消耗的影响，不符合实际运行的环境，从而导致计算结果不准确。本发明将考虑三维风对飞行地速的影响，进而建立三维风影响下BADA爬升阶段燃油消耗模型。

风速大小Vwind和风速方向Dwind，其中风速方向以真经线正北方向为0°，顺时针为正。通过查询气象数据，可以获取不同地区不同高度的风数据，包括风速大小和风速方向。

为研究三维风对飞机飞行的影响，首先需要根据风速大小Vwind和风速方向Dwind，计算得到风速在地面坐标系中的投影矢量[uwg vwg wwg]^T，即：

uwg＝Vwindcos Dwind (10)

vwg＝Vwindsin Dwind (11)

wwg＝0 (12)

有侧风时，飞机的地速在[u v w]^T机体坐标系中的投影矢量VGS为：

其中，Lbk，Lbg分别为：

[uwg vwg wwg]^T可由式(10)、(11)和(12)计算得到，即飞机的地速为：

由式(3)和(4)可得加入侧风后的阻力与推力计算公式如下：

再由式(1)、(2)和(6)可计算加入侧风后的燃油消耗量，公式如下：

基于上述优化，下面对离场连续爬升运行模式性能进行分析。

离场连续爬升是一种飞机运行模式，其离场程序根据飞机的性能进行飞行剖面的优化设计，满足的ATC放行许可，使飞机在爬升过程中，能够以最优空速和最佳引擎推力参数爬升至初始巡航高度。基础的连续爬升离场程序设计前提是所有飞机爬升率都不受限制，这就要求足够的垂直空域来保证连续爬升运行模式不受干扰。

传统离场爬升和离场连续爬升两种运行模式，采用如下两个运动学模型描述。爬升阶段运动学模型如下：

平飞阶段运动学模型如下：

其中，D，T分别为式(16)和(17)的计算结果，h为飞行高度，α为飞行迎角；原点O位于飞机质心，OX轴指向飞机的地速方向，OZ轴位于包含OX轴的铅垂平面内且垂直于OX轴，代表飞行高度，OY轴垂直于OXZ平面；Vwind1，Vwind2，Vwind3分别为三维风在OZ轴，OX轴，OY轴上的分量。

根据两阶段的运动学模型进行对比分析，爬升阶段将采用一定的倾斜角进行爬升，飞行高度随着飞行时间改变而增加；而平飞阶段倾斜角为0，飞行高度不随着飞行时间的变化而变化。连续爬升阶段整个过程均采用爬升阶段的运动学模型，按照一定的倾斜角及爬升梯度一直爬升到初始巡航高度，中间无平飞阶段。而传统爬升阶段整个过程采用爬升阶段与平飞阶段相结合的运动学模型，先按照一定的倾斜角及爬升率爬升到指定高度，接着在该高度进行平飞，平飞一段距离后再爬升，依次循环至爬升到初始巡航高度。

基于以上连续爬升运行特点，本发明将按照变换固定爬升角与爬升梯度进行轨迹模拟飞行，该飞行阶段全程持续爬升无平飞增速阶段，以致飞机在最短时间内达到最优空速和初始巡航高度。在飞行轨迹基础上加入前面所建立的燃油消耗优化模型，将计算结果与传统爬升耗油量进行对比分析。

下面，实施例中采用青岛流亭国际机场离场为研究对象，加入山西太原武宿国际机场离场进行模型的进一步验证。

首先获取A320机型的QAR青岛离场实际运行数据，在编制青岛离场飞行轨迹仿真程序的基础上，并结合上述理论模型，建立五组对比实验，通过对比实验数据分析，验证本发明的理论模型相比于以往燃油消耗评估模型更优。然后分析了飞机质量差异以及爬升角度不同对燃油消耗的影响，最后分析了空客A320与空客A321不同机型对燃油消耗的影响。具体步骤如下：

步骤1、数据获取和准备

通过仿真编程结合航路点信息，仿真出飞机的飞行轨迹，再通过所仿真出的飞行轨迹中参数，代入BADA爬升阶段燃油消耗模型中，最终进行燃油消耗理论计算。

进行燃油消耗计算之前，我们需要先模拟出飞机飞行轨迹，获取飞机飞行过程中的速度、高度、航向、飞行距离等飞行参数。由于燃油消耗理论计算结果需与QAR数据进行对比验证，所以在飞行轨迹模拟时应采用QAR中实际飞行离场航线。所获取的QAR数据为青岛-虹桥航线，根据青岛-虹桥飞行计划，选取青岛机场离场爬升阶段的航路点信息，其中模拟的飞行速度、爬升率均和QAR数据近似，具体爬升航路点信息如表2所示。基于QAR数据，本算例选取机型A320，假定飞机质量为63t，爬升角为5°，机翼面积为122.6㎡。连续离场爬升和传统离场爬升两种运行模式的飞行剖面如图1所示。两种运行模式各个航段相关节点的信息表如表2和表3所示。

表2青岛机场传统离场爬升航路点信息表

表3青岛机场离场连续爬升航路点信息表

通过表2中信息可得出飞机从青岛跑道起飞，起飞速度为300km/h，起飞后沿着A1方向按照一定爬升率爬升至1000m的飞行高度，飞行速度保持300km/h，到达A1航路 点，进行平飞增速，飞行速度上升至560km/h后沿着A2方向进行爬升，到达A2航路点进行平飞增速阶段，最后继续爬升至7200m的初始巡航飞行高度，飞行速度为780km/h，爬升阶段结束。

通过表3中信息可得出飞机从青岛跑道起飞，起飞速度为280km/h，起飞后沿着A1方向按照一定爬升率爬升至1000m的飞行高度，到达A1航路点时，飞行速度上升为340km/h，再沿着A3方向按照一定爬升率爬升至3200m的飞行高度，到达A3航路点时，飞行速度上升为600km/h，最后继续爬升至7200m的初始巡航飞行高度，飞行速度为780km/h，爬升阶段结束。整个连续爬升阶段与传统爬升阶段相比，无平飞航段，速度增加过程均在爬升航段完成。

利用编制的计算机程序，结合表2信息，以青岛机场基准点为坐标原点的直角坐标系，可仿真出青岛离场爬升阶段的飞行轨迹，仿真出的飞行轨迹信息具体包括仿真时间、坐标点、飞行高度、航向、飞行速度、真空速以及音速，如表4所示。仿真轨迹与QAR真实飞行轨迹如图2所示。

表4模拟飞行轨迹信息表

结合仿真飞行轨迹信息中的飞行速度和式(5)可求出飞行轨迹中各点的升力系数；再由升力系数与阻力系数的关系求出各点的阻力系数；结合式(4)求出阻力的大小，其中大气密度ρ、温度T以及大气压强p均根据2.1节中气象参数随飞行高度的变化公式所得出；结合式(3)求出推力的大小；最终结合式(1)和(2)求出飞行轨迹中各 点的燃油消耗量。

步骤2、五组对比实验

本算例以青岛离场为例，对爬升阶段下飞机的燃油消耗进行讨论，分为以下五组对比实验：1)采用空客A320机型利用实验对比的方法验证模型中气动参数的优化使得模型更加精确；2)在气动参数优化基础上验证加入侧风使得模型更加精确，并将燃油消耗优化模型所计算的航班燃油消耗量理论值与某航空公司的航班实际运行QAR数据作对比，以验证所优化的BADA爬升阶段燃油消耗模型是否可行；3)计算连续爬升阶段燃油消耗量理论值，与传统爬升阶段燃油消耗理论值进行对比分析，并分析了改变爬升角和飞机质量的燃油消耗差异。

五组对比实验具体如下：

(1)优化气动参数实验及结果分析。

相关学者所提出的燃油消耗模型中，气动参数往往采用查阅由风洞试验方法获取的静态图表关系，该方法的数据源自理想化的数据。在空客A320性能手册获取该静态图表关系如图3所示。

现设计以下实验将以往的方法与我们所提供的真实QAR数据拟合方法进行对比分析，即：1)在基于BADA爬升阶段燃油消耗模型基础上，气动参数中阻力系数与升力系数的大小通过查阅由风洞试验方法获取的静态图表关系，如图3所示，进行取点，加入模型中进行燃油消耗计算；2)气动参数中阻力系数与升力系数采用本发明提出的基于QAR数据最小二乘法进行函数拟合所得出的关系式加入模型中进行燃油消耗计算。

结合图8所示，将上述实验计算结果分别与QAR数据作对比，说明采用基于QAR数据最小二乘法进行函数拟合得出的气动参数关系式比查阅由风洞试验方法获取的静态图表关系更精确。

接下来将对QAR数据结合MATLAB软件采用最小二乘法进行多项式拟合。前文已给出不同马赫数所对应的多组阻力系数与升力系数数据。实施例中以0.7马赫数为例，对阻力系数与升力系数关系表达式进行拟合。其余马赫数所对应的拟合关系按照同样的方法获得。将A320飞机的QAR数据挑选出0.7马赫数所对应的升力系数与阻力系数，将其导入Origin软件，利用Curve Fitting功能拟合出幂函数、指数函数、一次至多次多项式函数。

幂函数拟合结果图像如图4所示。根据拟合结果(图中左上角)，可得出a＝0.04886，b＝0.67968，其中a值表示幂函数的系数，b值表示幂函数的指数，即拟合出的幂函数表达式为f(x)＝0.04886×x^0.67968，残差平方和(SSE)为2.827×10^-5，拟合优度(R-square)为0.9674。根据图4可直观看出，所拟合出的幂函数曲线与QAR数据点偏差较大。按照同样方法可得出指数函数与多项式函数(从一次到三次)的拟合结果与拟合图像。将拟合结果汇总到表中，见表5。

表5拟合结果汇总表

根据表5结果中，可得出各函数类型的拟合表达式、拟合优度及残差平方和值。根据第3节所述，残差平方和和拟合优度是用以反映变量之间相关关系密切程度的统计指标，残差平方和值越小，拟合优度值越接近于1，拟合结果越精确。由表中结果可得出多项式函数中二次函数和三次函数残差平方和值远远小于幂函数、指数函数及一次函数，即二次函数和三次函数拟合精度在残差平方和这个判断指标上来看要比其他所拟合的三种函数高。并且二次函数和三次函数拟合优度均为1，幂函数为0.9674，指数函数为0.9919，一次函数为0.9771，通过比较可得二次函数和三次函数拟合精度在拟合优度这个判断指标上来看要比其他所拟合的三种函数高。结合拟合优度和残差平方和值这两个判断标准，可得出二次函数与三次函数均可作为数据点的关系表达式。

如图4所示，前面已经将幂函数图像与QAR数据点放在图像中进行对比。与此类似，现分别将指数函数、多项式函数与QAR数据点放在图像中对比，如图5和图6所示。通过图4、图5和图6中各函数拟合对比图显示，可以宏观看出幂函数、指数函数以及一次函数与数据点偏差较大，重合度很低，二次与三次函数图像几乎重合且与数据点较吻合，进一步验证二次函数和三次函数可作为数据点的关系表达式从而精确表达出QAR数据点。图6中左上角为多项式拟合结果。

实施例中亦研究次数大于三次的多项式拟合，拟合优度均为1，残差平方和值与二 次、三次近似，略小于二者。但由于次数过高会强制曲线穿过样点，有失真实性，且容易产生龙格现象，造成高频振动。基于此原因，我们忽略高次的多项式函数而选用二次函数作为数据点的拟合关系表达式。所以0.7马赫数所对应的拟合关系表达式为：

按照同样的方法可拟合出不同马赫数下阻力系数与升力系数的关系表达式，如表6所示。

表6拟合关系表

将以上关系表采用插值方法获取马赫数、阻力系数、升力系数三者之间关系式如下：

三者之间关系图像如图7所示。

将得出的马赫数、阻力系数以及升力系数三者之间关系式与查表风洞试验中所获得的阻力系数与升力系数数值分别代入BADA爬升阶段燃油消耗模型中，进行计算。两种方式各点燃油消耗计算结果如图8所示。

图8显示的是飞行过程中以每4秒划分为一个飞行阶段的燃油消耗值，飞行过程为720秒，共计180个飞行阶段。黑色曲线为基于查阅由风洞试验方法获取的静态图表关系代入BADA爬升阶段燃油消耗模型中所计算的燃油消耗值，红色曲线为采用拟合方法所得出的阻力系数与升力系数关系代入BADA爬升阶段燃油消耗模型中所计算的燃油消耗值，蓝色曲线为QAR数据。通过图像直观看出，黑色曲线各点均位于蓝色和红色曲线的下方，且红色曲线与黑色曲线相比红色曲线更接近于蓝色曲线，即采用拟合方法比采用风洞试验方法更精确。

下面将飞行过程中720秒以72秒为一个飞行阶段，划分成10个飞行阶段，将各阶 段的燃油消耗值进行计算得出表7。

表7燃油消耗对比表(单位：kg)

通过表7进行量化分析可得，各个飞行阶段采用风洞试验所计算的燃油消耗均小于采用拟合方法计算的燃油消耗值和QAR数据值，这是由于采用查阅由风洞试验方法获取的静态图表关系属于理想情况下，采用试飞数据获取二者之间的关系，未考虑由于飞机性能衰减造成的额外耗油。采用风洞试验计算的燃油消耗准确度为965.2/1116×100％＝86.5％，采用拟合方法计算的燃油消耗准确度为1014.5/1116×100％＝90.1％，通过燃油消耗准确度对比，采用基于QAR数据最小二乘法进行多项式拟合得出的气动参数关系式比采用风洞试验所给出的关系式更精确，使得BADA爬升阶段燃油消耗模型更优化。

利用表7中数据，将10个飞行阶段中QAR数据分别与采用风洞试验以及采用拟合方法所得到的燃油消耗值做差值，将计算结果绘制到图表中，如图9所示。从图9中可看出，10个飞行阶段中每个飞行阶段的QAR数据记录的燃油消耗量与拟合方法计算的燃油消耗量的差值均小于QAR记录的燃油消耗量与风洞试验方法计算的燃油消耗量的差值，即每个飞行阶段采用拟合方法计算的燃油消耗值与风洞试验相比更接近QAR值，因此进一步验证了采用拟合方法比风洞试验方法更精确，且各个飞行阶段均满足。

(2)加入侧风参数差值比较图中可看出实验及结果分析。

在实际运行中，侧风对飞机的飞行航迹产生较大影响，也直接影响到离场的燃油消耗量。因此在优化气动参数基础上，我们加入侧风对BADA爬升阶段燃油消耗模型的影响，将QAR数据中风的数据加入到模型中进行理论计算，并与QAR中燃油消耗量对比，计算出所提出的燃油消耗优化模型精确度，验证是否可行。前面我们分析了三维风对燃油消耗的影响，将QAR数据中俯仰角θ、偏航角风速Vwind以及风向Dwind代入式(13) 中，计算得出加入三维风的地速VGS，再将地速加入BADA爬升阶段燃油消耗模型中可得各点燃油消耗结果如图10所示。

图10显示的是飞行过程中以每4秒划分为一个飞行阶段的燃油消耗值，共计180个飞行阶段。再将飞行过程中720秒以72秒为一个飞行阶段，划分成10个飞行阶段，将各阶段的燃油消耗值进行计算得出表8。

表8青岛机场理论计算与QAR数据对比表(单位：kg)

由于本实验是在拟合多项式基础上加入的侧风影响，所以本实验的燃油消耗模型是最终优化的模型。现将该模型计算结果与QAR计算结果作对比，判断模型是否可行。将各点燃油消耗量相加可得整个爬升阶段总的燃油消耗量为1041.6kg，QAR数据中整个爬升阶段总的燃油消耗量为1116kg，即可得总的燃油消耗模型精确度为1041.6/1116*100％＝93.3％，各个飞行阶段的精确度计算结果如表8所示，精确度结果显示所提出的优化后的BADA爬升阶段燃油消耗模型在各个飞行阶段均计算精确度高，模型可行。

与只采用拟合方法计算燃油消耗相比精确度增加了93.3％-90.1％＝3.2％。这是由于加入侧风影响后，根据式(7)地速会发生改变，从而导致阻力及推力发生改变，再由式(2)和(6)可得最终导致燃油消耗发生改变，这使飞机的燃油消耗更贴近于真实环境下的燃油消耗，导致计算结果更加精确。

由于前面实验结果是在青岛仿真轨迹基础上加入优化后的BADA爬升阶段燃油消耗模型进行计算的，所以存在仿真轨迹与QAR轨迹相比有误差的问题，从而导致燃油消耗计算结果也存在一定误差。现使用山西太原武宿国际机场离场爬升QAR轨迹数据，代入优化后的BADA爬升阶段燃油消耗模型中，计算结果与该QAR油耗数据作对比，如图11所示。

该爬升阶段为1120秒，以112秒为一个飞行阶段进行划分，共计10个飞行阶段，各飞行阶段的燃油消耗值进行计算得出表9。

表9山西太原武宿国际机场理论计算与QAR数据对比表(单位：kg)

本实验结果是在采用QAR轨迹数据基础上加入所优化后的BADA爬升阶段燃油消耗模型可得，可以单纯的验证模型的准确性，同表8中数据以及图10中图像对比可得，根据所优化后的BADA爬升阶段燃油消耗模型计算出的结果与QAR油耗值相差1645-1578.9＝66.1，模型精确度为1578.9/1645*100％＝96％,且从各个飞行阶段精确度可看出所优化的模型可行，计算精确度较高。

(3)对比分析两种离场爬升模式燃油消耗量。

前面已验证了优化后的离场爬升阶段燃油消耗模型计算结果对比QAR真实数据精确度较高，模型可行。在此基础上计算离场连续爬升阶段的燃油消耗，与前面所计算的传统离场爬升阶段的燃油消耗进行对比分析。

首先根据传统离场爬升与离场连续爬升两种运行模式的特点以及表2传统离场爬升航路点信息表，可得出青岛机场离场连续爬升航路点信息表如表3所示。

根据国际民航组织颁布的离场连续爬升运行手册可得，离场连续爬升运行模式的爬升梯度为60～300m/nm，即3.24％～16.2％，实施例中选取离场连续爬升梯度为10％。传统离场爬升运行模式参照青岛机场标准离场程序可得其爬升梯度不超过4％，实施例中再结合QAR数据中轨迹数据，根据爬升阶段中不同飞行阶段选取与QAR数据中近似的传统离场爬升梯度。其中两种离场爬升运行模式飞行速度均需满足ATC约束，即FL100高度下飞行速度不能超过250kt。

选取好离场爬升性能参数之后结合表3航路点信息，利用VB编程仿真出连续离场航路的飞行轨迹，其中包含飞行高度、飞行速度、航向等参数。在此基础上加入前面所 建立的优化后的BADA爬升阶段燃油消耗模型，可计算出连续离场航路的燃油消耗量理值。将连续离场爬升与传统离场爬升燃油消耗计算值进行对比如图12所示。通过分析可得，由于离场连续爬升阶段按照所设定的爬升梯度一直爬升到初始巡航高度，该过程通过式(9)可得出此过程的推力比平飞过程的推力要大，从而导致爬升阶段的燃油消耗比平飞过程要大。即从青岛离场一直爬升到初始巡航高度点，该过程一直处于燃油消耗量较大的状态，后面进行平飞直至TOC1航路点。而传统爬升模式采用的是爬升与平飞相结合的运行方式，即在图中可看出红色曲线呈现高低不平状态，图中中间平稳段表示平飞航段。

由于爬升模式不同，各点的燃油消耗量也有很大差别。现比较两种离场爬升模式总的燃油消耗量，将离场连续爬升模式各点燃油消耗量相加为913kg，与前面所计算的传统离场爬升模式燃油消耗总量1041.6kg相比减少128.6kg。可得采用离场连续爬升离场比采用传统离场爬升离场要节省燃油。这是由于离场连续爬升运行模式爬升梯度大于传统离场爬升模式爬升梯度，即离场连续爬升运行模式总的爬升时间要小于传统离场爬升，前面已经分析爬升阶段的燃油消耗要大于平飞阶段，所以离场连续爬升运行模式燃油消耗量要小于传统离场爬升运行模式。

(4)飞机质量和爬升角度对燃油消耗影响分析。

在上述实验基础上，进一步分析飞机质量以及爬升角度的不同对燃油消耗的影响。

首先分析飞机质量该因素对燃油消耗的影响。参照BADA数据库可得空客A320最大起飞重量(MTOW)为77000kg，空载为42400kg，所以选用70％、80％、90％以及100％最大起飞重量(即53900kg、61600kg、69300kg以及77000kg)分别进行燃油消耗计算，并进行量化分析。该计算过程中，考虑了飞机质量由于燃油消耗量的产生从而导致的变化，更加符合真实运行情况。燃油消耗理论计算结果如图13所示。从图13中对比可看出，飞机质量高的曲线均位于飞机质量低的曲线下方，即燃料量随总飞行距离以及飞行质量的增加而增加。这是由于飞行质量的增加，通过式(5)可得升力系数增大，从而导致阻力系数的变化，再由式(3)导致推力的增加，最终使得燃油消耗增大。通过图13中趋势可看出，随着飞行距离的增加，飞行质量对燃油消耗的影响逐渐增大。因此起飞前预测出精确的燃油消耗量，可以避免飞机配载多余的燃油量，从而避免不必要的飞机质量导致燃油消耗的产生，即以防“油耗油”现象的发生。

飞机爬升角度对燃油消耗的影响。前面仿真轨迹研究采用的爬升角为5°，在此基础 上选用爬升角为8°和10°来分析爬升角度对燃油消耗的影响(BADA数据库[5,32]中对爬升角限制为在低重量下不超过18度，高重量下不超过15度)。不同爬升角仿真出的燃油消耗值如图14所示。从图14中对比可看出，爬升角度的增大会导致燃油消耗量的增加。这是由于爬升角度的增大，根据式(5)及式(3)会导致推力增大，进而使得燃油消耗量增大。管制员指令往往是导致爬升角变化的主要因素，由于空域交通流的影响，管制员为了协调飞机在空域中交通安全间隔问题，从而发出快速爬升的指令，进而导致飞行员改变爬升角度。

(5)不同机型对燃油消耗影响分析。

与前面方法一致，针对空客A321机型的QAR数据将气动参数进行拟合，拟合结果如表10所示。

表10空客A321拟合关系表

同样将以上关系表采用插值方法获取马赫数、阻力系数、升力系数三者之间关系式如下：

三者之间关系图像如图15所示。

将拟合得出的马赫数、阻力系数与升力系数关系式分别代入优化后的BADA爬升阶段燃油消耗模型中，进行计算。将计算结果与相同运载条件下的空客A320机型计算结果进行对比，如图16所示。从图16中可看出，随着飞行距离的增加，空客A320机型在爬升阶段中燃油消耗量先大于空客A321机型，到达指定飞行距离后，燃油消耗量空客A320机型便小于空客A321机型。即在短距离爬升飞行过程中，空客A321较空客A320更省油，远距离爬升飞行过程中，空客A320较空客A321更省油。空客A321机型燃油消耗量为1063.6kg，空客A320机型燃油消耗量为1041.6kg，节省22kg燃油。这是由于 不同机型存在性能差异，导致气动参数之间的关系存在不同，从而导致两种机型燃油消耗量各异。

基于上述五组对比实验，对实验结果总结如下：

气动参数优化实验中，根据QAR数据阻力系数与升力系数的关系曲线趋势，确定了符合该趋势的幂函数、指数函数以及多项式函数作为拟合函数。通过拟合优度(R²)及残差平方和(SSE)这两个判别拟合结果优劣的参数，最终确定最优拟合函数为二次函数(式(28))，将拟合结果代入优化后的BADA爬升阶段燃油消耗模型中，燃油消耗量理论计算结果为1014.5kg，与QAR数据相比精确度为90.1％，采用查阅由风洞试验方法获取的静态图表关系的燃油消耗量理论计算结果为965.2kg，与QAR数据相比精确度为86.5％，QAR数据实际燃油消耗量为1116kg，通过计算数据可得，优化后的BADA爬升阶段燃油消耗模型中采用拟合方法比采用风洞试验方法来获取气动参数之间的关系更精确。

在优化气动参数基础上，我们加入侧风对燃油消耗模型的影响，将QAR数据中风的数据加入到模型中进行理论计算，燃油消耗理论计算结果为1041.6kg，与QAR数据相比精确度为93.3％，模型可行。与只采用拟合方法计算燃油消耗相比精确度增加了93.3％-90.1％＝3.2％，这是由于爬升阶段燃油消耗模型中加入侧风的影响会更贴近实际飞行环境，使得模型更加优化，计算结果精确度更高。此外，采用山西太原武宿机场QAR轨迹数据加入模型中，排除由于仿真轨迹误差所带来的燃油消耗误差，最终计算结果为1578.9kg，与QAR数据1645kg相比差值为66.1kg，精确度为96％，更加验证模型可行。

在前面已经验证所优化的BADA爬升阶段燃油消耗模型可行的基础上，计算离场连续爬升阶段的燃油消耗模型，计算结果为913kg。传统离场爬升阶段的燃油消耗计算结果为1041.6kg。两种离场爬升模式相比，离场连续爬升运行模式燃油消耗量减少了128.6kg，即离场连续爬升运行模式比传统离场爬升运行模式更节省燃油。

最后，考虑了飞机质量、爬升角度以及不同机型对燃油消耗的影响，通过计算结果可得，燃油消耗根据飞机质量的增加而增大，且随着飞行距离的增加，飞机质量对燃油消耗的影响逐渐增大。同样，燃油消耗伴随着爬升角度的增大而增大。空客A321与空客A320机型相比，在短距离爬升飞行过程中，空客A321较空客A320更省油，远距离爬升飞行过程中，空客A320较空客A321更省油，算例计算结果为空客A320较空客A321节省22kg燃油。

综上所述，本发明在分析QAR实际飞行数据的基础上，拟合离场爬升阶段燃油消耗模型中气动参数之间的函数关系；对侧风建模，加入燃油消耗评估模型中，并建立离场持续爬升运行模式的运动学模型。通过青岛机场离场爬升实验分析，采用改进的BADA爬升阶段燃油消耗模型计算离场爬升阶段的燃油消耗量，与QAR数据进行对比，结果显示比风洞实验计算结果精确度提高了3.6％；考虑侧风的燃油评估实验结果表明，理论模型计算结果与QAR数据精确度为93.3％。利用上述理论模型，计算连续爬升运行模式燃油消耗量小于传统爬升运行模式，同时分析了飞机质量差异以及爬升角度不同对燃油消耗的影响，最后分析了空客A320与空客A321不同机型对燃油消耗的影响。由此可见，本发明所提出的基于飞行数据分析的飞机离场燃油消耗评估方法的主要成果包括：1)基于QAR数据拟合的方法可以更加精确获得气动参数之间的数量关系；2)建立了侧风动力学模型，并结合拟合获取的气动参数函数关系，并修正了BADA爬升阶段燃油消耗模型；3)采用上述改进模型，利用五组分组对比实验，与QAR实际运行数据对比，验证了本发明提出的燃油消耗评估模型，相对于传统的BADA爬升阶段燃油消耗模型，精确度提高了3.6％。并在上述实验基础上，进一步计算验证了在飞机质量、爬升角度变化以及不同机型对燃油消耗的差异。通过本发明建立的基于BADA数据库的飞机离场燃油消耗评估模型，可以精确控制燃油加载量，避免飞行前所加油量过多从而导致“油烧油”现象的发生，从而减少燃油成本。

以上所述仅为本发明的优选实施例而已，并不用于限制本发明，对于本领域的技术人员来说，本发明可以有各种更改和变化。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。