一种基于MPC算法的独立悬架结构车辆控制方法与流程
本发明涉及现代智能控制技术领域与运筹学,具体涉及的是一种具有2自由度的独立悬架结构车辆控制方法。
背景技术:
模型预测控制(modelpredictivecontrol,mpc)是20世纪60年代初期发展起来并日趋完善的现代控制理论,具有极强的性能指标和系统精确的理论设计方法,在航天航空、制导等领域中获得了卓越的成就。但是在应用于工业过程控制时却难以轻松获得成果。究其原因,在工业应用受阻主要问题在于工业环境因素复杂建立控制方法的矩阵维数较多,模型预测对处理器性能要求过高,预测时域一旦过大就会导致一般的工控机数据处理速度变慢,对于工业而言又难以为此支付高昂的成本从而难以实施,但在投入成本不低汽车行业,尤其是对近年来加入智能计算机系统的高档车辆来说却有着有力的优势。
面对理论发展与实际应用之间的不协调,各国专家学者投入了大量的心血用以研究mpc的优化与应用。在著名国际研讨会nmpc05与nmpc08上人们认真的评估了非线性模型预测控制的现状、未来方向和待解决的问题。(findeisonr,allg~owerf,bieglerlt.assessmentandfuturedirectionsofnonlinearmodelpredictivecontrol.berlin:springer,2007)
模型预测控制(mpc)当前控制动作是在每一次采样后通过求解一个有限时域开环最优控制问题而获得。过程的当前状态作为最优控制问题的初始状态,解得的最优控制序列只实施第一个控制作用。在整个控制过程中最难以实现的是每一次控制时序之间要进行二次型最优滚动求解,每个时序都要重新计算,这使得工程量极其巨大,如何针对这一问题进行改进从而将mpc融入工程化应用也是本文的一个重要部分。
中国专利cn107399364a公开了一种多地隙自转向机构,其机械设计使得在转向时具有极大的先天优势,近两年在江苏海安投产效益丰厚,但由于其结构特殊工况复杂非线性和各种不确定因素使其建模困难不易控制,核心还停留在pid控制中,使得系统不得不附加外部手段进行辅助控制,给生产成本带来了巨大困扰给用户的使用带来极大的不便。
技术实现要素:
本发明的目的是对独立悬架车辆进行控制从软件算法角度对其操控性能进行提升,进一步解放硬件约束,期望克服现有技术方法的不足,做到控制简单、可控性好、实用性强并且易于维护,为此提出一种基于mpc((modelpredictivecontrol,模型预测控制)算法的控制方法。
本发明采用的技术方案是:基于mpc算法的独立悬架车辆控制方法
包括以下步骤:
步骤1,获取车辆模型参数,建立对象较为精确的牛顿力学微分方程;步骤2,对各方程进行线性化优化,简化微分方程并由此建立微分方程组;步骤3,对速度和加速度建立逐点线性化模型;步骤4,根据步骤2和步骤3建立mpc状态空间方程组;步骤5,基于步骤4,对系统的能控性和能观性与稳定性进行分析;步骤6,对步骤4线性连续状态空间方程组进行离散化;步骤7,建立最优二次型指标求解最优控制方案;步骤8,应用最优解的第(k+1)组策略,并采样更新各参数,然后进行下一时刻滚动优化。
进一步,所述步骤1具体方法是:
步骤1.1,获取电机参数补充电机输入电压与输出转矩和转速的关系方程。
步骤1.2,根据刚体力学建立车轴转动时角度与转矩的微分方程。
步骤1.3,根据整车的运动学方程建立输入的控制电压与车速、转弯半径以及转向时向心加速度的关系。
进一步,所述步骤2具体方法是:
对于精确的物理微分方程模型来说往往都是非线性的系统很难直接用现代控制理论来描述。本文结合研究对象特性给出一种具有针对性的线性化方法。
进一步,所述具有针对性的线性化方法具体是:
步骤2.1,对车轴的微分方程进行初步线性优化,忽略了直流电机内阻带来的影响,排除了一部分非线性因素。
步骤2.2,用matlab模拟形成的数值误差分析,经判定在允许范围内可以近似根据等价无穷小原理对转弯向心加速度和转弯半径表达式进行线性优化。
步骤2.3,根据步骤2.2的结论对整车车速进行线性优化并确立了前后轴的输入电压对车速产生的影响。
进一步,所述步骤3具体方法是:
对于车身速度变量v,表达式不仅是非线性的而且是状态变量x和控制变量u的耦合形态,对此以往文献往往采取整个系统一起泰勒展开线性化,这样不仅让其他线性部分变得精确度降低还让计算过程变得更加复杂,并且在本方法中加速度是关于速度的平方的变量而且与其他状态变量耦合,无法直接建立方程,为此本方法创新性采用无穷级数分解的方法将其在当前k时刻展开,分离为线性部分和高阶无穷小部分,线性部分取一次项,无穷小部分是关于x和u误差的二阶无穷小。由此不仅将v线性化更解开了x和u的耦合一举两得。如上所述对加速度
v=avx+bvu+dv
其中v是车身的速度,
进一步,所述步骤4具体方法是:
以往的文献中常常直接把微分方程组对应系统自由度建立mpc姿态稳定器而不是完整的控制器,常因为速度的加入使得方程无法建立为满秩方阵进而使得系统方程具有不完全可控因素,从而放弃了速度的精确控制另做闭环。本方法创新性得引入形式变量解决这一问题。
步骤4.1,本方法大胆加入形式状态变量s,其物理意义为车辆行驶过的路程,在本方程中没有太大的含义但是其引入使得其导数v进入了系统表达式,由此建立起包含速度和向心加速度以及系统姿态稳定的线性连续状态空间方程组:
其中x是车的状态变量,
步骤4.2,虽然这样造成了系统矩阵atx的不满秩,但是经过分析其不完全可控的对象是行程s,然而s对系统没有有多大的影响是个形式变量,主要还是要关注前后轴角度的协调配合以及其差值。所以初步分析本方法可行,令状态变量为
进一步,所述步骤5具体方法是:
分别对步骤4中的线性连续状态空间方程组进行rank(btu,atxbtu,…,atx5btu),rank(c,cbtu,…,c5btu),det(λi-atx)=0的计算从而估计系统的能控性能观性和稳定性。其中rank(*)代表矩阵求秩操作,det(*)代表矩阵求特征行列式操作。
进一步,所述步骤6具体方法是:
工业控制器往往以时序作为控制核心,为此必须把连续时间方程组变为离散方程组,同时为了减少数据堆积与引入积分环节消除静态误差并且解决状态变量冗长多余的问题,采用增量式书写,得到了如下增量式离散方程组:
其中δ代表前后时刻的变化量,δx(k)是与x(k)同维数的状态增量,δu(k)是与u(k)同维数的控制输入增量,δdp(k)是与dp(k)同维数的补偿量增量,a、bu、bp、c分别为atx、btu、btp、ct对应的离散化表达式,|*|(k)表示k时刻的状态变量。
进一步,所述步骤7具体方法是:
首先建立针对目标优化的二次型函数j,不同于以往将最优二次型的权值都设置为1的方法,本方法针对具体对象给出了更具体更有效的权值参考系数从而更有针对性得进行控制方案制定,使车辆的行动更符合预期工作要求提高了行车过车中的稳定性。
进一步,所述最优二次型及其权值设定的具体方法是:
步骤7.1,通过建立如下的二次型优化目标可以减少离散化方程组的求解复杂度降低不必要的计算量,其中根据重要程度设置加权矩阵的数值从0到1分别为不重要和重要。
minj=‖γy(yp(k+1|k)-r(k+1))‖2+‖γuδu(k)‖2
其中j为目标函数,其中,γy是对预测模型与参考输入误差的加权矩阵,γu是对控制输入增量的加权矩阵,r(k)为给定输出r(k)的参考序列,δu(k)为δu(k)的序列。
在本方法创新性在于针对性的分析本案例,通过考虑控制变量的重要性调节最适合对象的权重系数。最优先考虑的是车辆前后行动的一致性,所以对θ的权值应当设计为1非常重要,其次是前后轴偏转角α和车身速度v分别为0.8比较重要,最后针对无人操作的喷雾车舒适性可以适当放松,δu(k)的调节平缓性不那么重要选取0.3。
其中设置约束条件前后轴转角不能超过±30°,车速不得高于限速且不得低于工作最低速,控制电压不得低于起转电压。
步骤7.2,将mpc约束问题精简为标准对偶化形式,由于在步骤7.1中设计γyγu均为正定矩阵,此问题符合kkt原则,其解具有唯一最优性。解这个二次型规划获得最优预测控制方案。
进一步,所述步骤8具体方法是:
将步骤7得到的预测最优解的第一组时序应用到控制时序,同时将步骤3中线性化后的矩阵进行更新迭代,同时更新由此而带来随后的二次型的矩阵迭代。
本发明的有益效果是:
本发明针对的对象一直以来使用传统的pid控制方法控制精度不高,适应能力低下,无法应对突发状况采取最优决策,仅仅依靠增设液压推杆和姿态辅助固定杆勉强进行辅助,但是随着时间推移,液压推杆和姿态辅助固定杆都出现一定程度的不可逆形变,同时这一操作大大提高了生产成本。这里提供一种基于mpc算法的独立悬架结构车辆控制方法。利用mpc算法对车辆行驶的信息进行记录采集并通过构建二次型最优化方法进行在线滚动求解,并应用第一组预测控制方法,同时滚动历史信息进行新一轮的控制序列求解。这样做的好处是在线滚动让控制器收集到足够有效和实时性的信息,矩阵序列和二次型系数参数一直随着滚动在线更新,由此可以更准确得给出控制序列从而提高系统的鲁棒性和自适应性。在以往的设计中,由于速度等变量是控制变量和状态变量的耦合,很多研究者将速度排除在控制器之外单独设立控制器,将姿态控制器和状态控制器分离,造成了系统复杂度的提升。本方法在设计mpc控制器时与其不同,不仅把姿态稳定作为设计标准,更重要的是先通过局部变量线性化将速度和加速度变量进行状态变量和控制变量的解耦,再引入形式变量s将其加入了二阶微分方程组中,将速度和姿态同时加入了mpc控制器。同时在对二次型优化函数的设计上本方法充分考虑了对象的特殊性,打破以往均衡权值的思想,对于精度要求等级不同的变量给予差别较大的权值分配,紧扣产品的实际理念让前后转角高度一致使得其前后轮毂行进时历经同一轨迹,对地面的碾压范围达到最小。最后获取kkt条件下方程的最优近似解。如此,本方法不仅针对转弯性能的控制提高了对象的可操作性还节约了姿态辅助推杆的额外设备需要,对农业自动化和机械智能化提供了技术支撑。
附图说明
下面结合附图和具体实施方式对本发明做进一步详细说明:
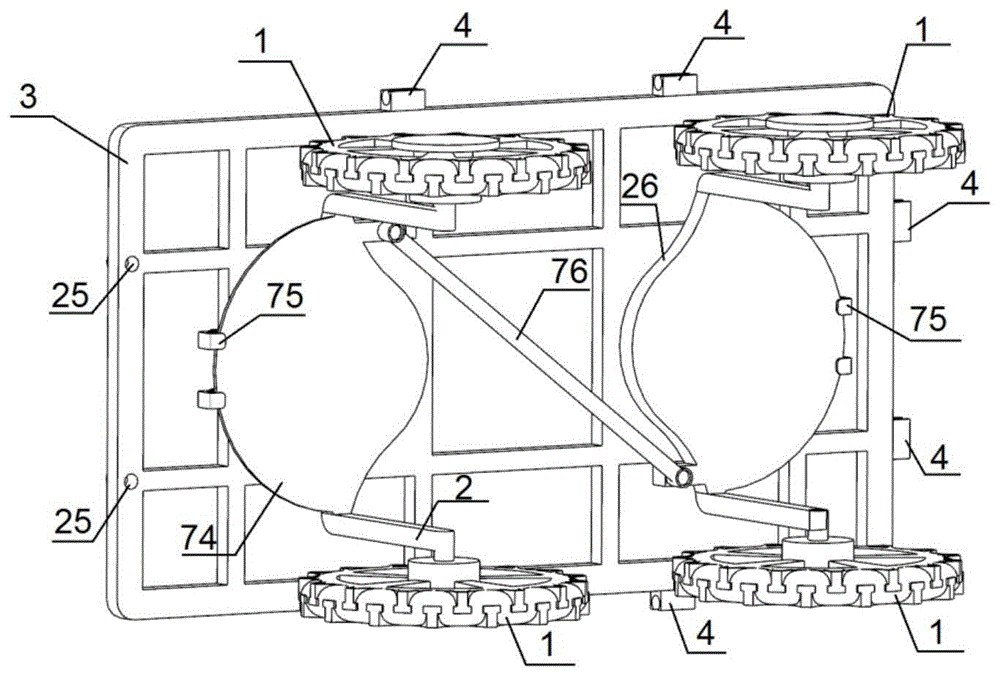
图1为车辆底盘示意图
图2为车辆转轴示意图
图3为整车力学加速度分析图
图4为整车受力分析图
图5为mpc控制系统流程图
具体实施方式
下面将结合本发明实施例中的附图,对本发明实施例中的技术进行清除、完整地描述。
图1为本发明的的研究控制对象——具有前后双重独立悬架结构的车辆模型(见专利号201710467123.x,一种多地隙自转向机构),采集所需的物理参量建立合适的物理模型;控制优化采用mpc算法;对mpc算法进行二次型最优规划对其进行最优解的快速获取;最终可以实现基于模型预测控制的二自由度独立悬架车辆控制。
步骤1,获取车辆模型参数,建立对象较为精确的牛顿力学微分方程。
(1)查阅手册获取电机相应参数数值建立各转轴微分方程
根据电机学公式可得直流电机扭矩与输入的关系为
其中t为直流电机输出的转矩,ia是电机电枢电流,ra是电机内阻,n为电机转速。
如图2所示的模型根据刚体力学建立车轴转动时角度与转矩的微分方程为:
其中
其方法为,分别固定前后转轴的中心点,以此展开思考发现只有摩擦力和电机的扭矩对车辆产生影响,以电机扭矩为改变角度的主要动力,以此构建刚体力学方程。
(2)根据整车的运动学方程建立输入的控制电压与车速、转弯半径以及转向时向心加速度的关系;
如图3所示根据圆周运动公式可得整车的运动学方程为:
其中α和β分别是前后轴的转角,a为车辆运动加速度,ac为车辆的向心加速度,at为车辆的切向加速度,l为前后车轴中心固定点的间距r为o点圆心到车轴的距离。
步骤2:对方程进行线性化优化,简化微分方程并由此建立微分方程组。
(1)对车轴旋转微分方程的线性优化。
在公式(3)(4)中忽略大功率直流电机内阻带来的调速影响,转轴微分方程可以线性简化表达为:
(2)用matlab模拟形成的数值误差分析,经判定在允许范围内可以近似根据等价无穷小原理对转弯向心加速度和转弯半径表达式进行线性优化;
设置死区空间,当α+β≤5°时默认直行状态有
(3)对整车车速进行线性优化并确立了前后轴的输入电压对车速产生的影响。如图4所示有运动学公式可得整车的运动学方程为:
其中r为轮胎半径,v为整车在车身朝向方向的速度,选取时采用了前后均衡下折中的方法,ianra表示四个电机各自的电枢电流与内阻,vn为第n个电机对应的车轮输出的线速度。由于对于较大功率的直流电机的内阻极小ianra相比远小于电枢u可以忽略不计则,并且根据直流电机机械特性曲线可知当输出转矩恒定就可以认为转速与电压呈近似正比,本模型在转弯时和匀速行驶时时根据无切向加速度的,即转矩不变。由此可得v的线性化方程表达式为:
步骤3:对车辆速度和加速度建立逐点线性化模型
对于车身速度变量v,表达式不仅是非线性的而且是状态变量x和控制变量u的耦合形态,采用无穷级数分解的方法将其在当前k时刻展开,分离为线性部分和高阶无穷小部分,线性部分取一次项,无穷小部分是关于x和u误差的二阶无穷小。由此不仅将v线性化更解开了x和u的耦合一举两得。
由于上文给出的状态空间表达式并不是完全线性的模型无法使用线性化模型理论知识进行设计姿态控制器,由此需要将非线性模型在操作时刻线性化,本发明采用在每一个操作时刻逐点线性化方法解决这一问题。
但是以往的控制算法几乎都是直接把整个方程进行逐点线性化,这样操作虽然看起来简单实际上把一些本身就线性的部分也进行了分割造成本来精确的数据反而成近似数据,降低了系统的可靠性和稳定性。由此根据观察,本文的6个变量中只有速度和加速度需要线性化,本文采用局部变量线性化的创新方法增加系统模型的精确度。
将上文给出的v的非线性模型改写为如下形式:
其中nx和nu代表变量x和u输入变量的维数,用泰勒公式展开将其在采样时刻k线性化,得到:
v=f(xk,uk)+acx(x-xk)+bcu(u-uk)+ek(16)
其中xk和uk分别是采样时刻的状态量与被控对象的输入值,均可在采样时刻通过测量得到,输入变量uk是已知的上一步优化的最优解应用。矩阵
(1)对速度进行处理,将v整理为v=avx+bvu+dv(17)
dv=f(xk,uk)-avxk-bvuk(18)
其中:
其中unk代表第n个电机在k时刻的输出;xk,uk代表在k时刻的状态以及控制信号;αk,βk代表k时刻前后轴的转角。
令
(2)同理对加速度
其中:
步骤4:根据步骤2和步骤3建立mpc状态空间方程组。
以往的文献中常常直接把微分方程组对应系统自由度建立mpc姿态稳定器而不是完整的控制器,常因为速度的加入使得方程无法建立为满秩方阵进而使得系统方程具有不完全可控因素,从而放弃了速度的精确控制另做闭环。本方法创新性得引入形式变量解决这一问题。
(1)由于速度和加速度在表达式中对x和u的耦合度很高而且速度与加速度不是简单的线性关系,方程一般难以建立也很难进行解耦控制,在之前的各种研究文献中大多使用与模型同等自由度个数的方程作为建立方程的依据,把速度和加速度排除在外,这样往往可以做成姿态控制器却不能实现对速度加速度等参数的控制,同时面临这个问题文献中往往闭口不谈或者归结到后期展望工作等等。
(2)本方法在此设计一种包含有加速度和速度的系统模型用以对车辆进行更全面的控制。令状态变量为
其中
其中
考虑造成系统控制矩阵atx的不满秩,但是经过分析其不完全可控的对象是行程s,然而s对系统没有有多大的影响是个形式变量,主要还是要关注前后轴角度的协调配合以及其差值,令状态变量为
步骤5:基于步骤4,对系统的能控性和能观性与稳定性进行分析。
(1)对上式所得的二自由度独立悬架系统的线性化状态空间模型进行能控性分析:若rank(btu,atxbtu,…,atx5btu)=6,由现代控制理论可知系统具有完全能控性。其中rank(*)代表矩阵求秩操作,det(*)代表矩阵求特征行列式操作。
(2)对上式所得的二自由度独立悬架系统的线性化状态空间模型进行能观性分析:rank(c,cbtu,…,c5btu)=6,由现代控制理论的充要条件可证明系统具有能观性。其中rank(*)代表矩阵求秩操作,det(*)代表矩阵求特征行列式操作。
(3)对上式所得的二自由度独立悬架系统的线性化状态空间模型进行稳定性分析:用matlab求取该状态空间方程的特征根det(λi-a)=0,发现不是所有特征根都具有实部,因此系统是开环不稳定系统。
(4)对上式所得的二自由度独立悬架系统的线性化状态空间模型进行求解分析,由于rank(atx)不是满秩方程无精确解,但是可以通过lr分解求取最优逼近解,事实上就是对速度和角度的协调控制并取最优控制方法,可以建立二次型线性约束进行求取。
步骤6:对步骤4线性连续状态空间方程组进行离散化。
为了方便工业控制器设计,需要把上文的连续时间状态空间方程组转化为离散时间控制系统,同时为了引入积分环节消除静态误差并且解决状态变量s冗长繁复的问题,令ts是系统的采样时间,将模型写成增量式:
其中δ代表前后时刻的变化量,a、bu、bp、c分别为atx、btu、btp、ct对应的离散化表达式,|*|(k)表示k时刻的状态变量,则该增量式离散模型与原模型有如下转换关系:
其中增量模型中δx(k)是与x(k)同维数的状态增量,δu(k)是与u(k)同维数的控制输入增量,δdp(k)是与dp(k)同维数的补偿量增量,且有:
δx(k)=x(k)-x(k-1)
δu(k)=u(k)-u(k-1)
δdp(k)=dp(k)-dp(k-1)
设定mpc的控制域为m,预测域为p,且满足m<p,并且做出如下假设:
1.控制域外控制量不变,即δu(k+i)=0,m≤i≤p-1。
2.补偿量在k时刻后不变,即δdp(k+i)=0,1≤i≤p-1。
令(k+1|k)表示当前时刻k对k+1时刻的预测值,根据模型预测的推导公式可得预测方程为:
yp(k+1|k)=iy(k)+sxδx(k)+suδu(k)+spδdp(k)(27)
其中各矩阵为:
状态变量δx(k)一般项只需把第k时刻减去(k-1)时刻即可,此处特别提及在δx(k)中δs以及其误差es为:
δs(k)=tsv(k)+es(k)
|es(k)|≤ts|v(k)-v(k-1)|
上式说明采样时间ts越小误差es越小。
步骤7:建立最优二次型指标。
首先建立针对目标优化的二次型函数j,不同于以往将最优二次型的权值都设置为1的方法,本方法针对具体对象给出了更具体更有效的权值参考系数从而更有针对性得进行控制方案制定,使车辆的行动更符合预期工作要求提高了行车过车中的稳定性。
步骤7.1,通过建立如下的二次型优化目标可以减少离散化方程组的求解复杂度降低不必要的计算量,其中根据重要程度设置加权矩阵的数值从0到1分别为不重要和重要。
minj=‖γy(yp(k+1|k)-r(k+1))‖2+‖γuδu(k)‖2
其中j为目标函数,其中,γy是对预测模型与参考输入误差的加权矩阵,γu是对控制输入增量的加权矩阵,r(k)为给定输出r(k)的参考序列,δu(k)为δu(k)的序列。
通过考虑控制变量的重要性调节最适合对象的权重系数。最优先考虑的是车辆前后行动的一致性,对θ的权值应当设计为1,其次是前后轴偏转角α和车身速度v分别为0.8,最后针对无人操作的喷雾车舒适性可以适当放松,δu(k)的调节平缓性选取0.3;
其中设置约束条件前后轴转角不能超过+30°,车速不得高于限速且不得低于工作最低速,控制电压不得低于起转电压;
步骤7.2,将以上mpc约束问题精简为标准对偶化问题样式。由于在步骤7.1中设计γyγu均为正定矩阵,此问题符合kkt原则,其解具有唯一最优性。解这个二次型规划获得最优预测控制方案。
(1)对离散化系统的要求可以通过二次型性能指标来表达,即输出尽量逼近目标并且希望控制幅度尽可能小,由此选择合适的目标:
minj=‖γy(yp(k+1|k)-r(k+1))‖2+‖γuδu(k)‖2(28)
其中:
umin≤u(k+j|k)≤umax,j=0,1,…,m-1
-δumin≤δu(k+j|k)≤δumax,j=0,1,…,m-1
ymin≤y(k+j|k)≤ymax,j=0,1,…,p
其中j是最优化木目标函数,r(k)为给定输出r(k)的参考序列,δu(k)为δu(k)的序列。γy是对预测模型与参考输入误差的加权矩阵,γu是对控制输入增量的加权矩阵,定义为:
γyj表示第j个输出误差的加权因子,其数值越大表示其参考比重越大,其结果精度越高,γuj表示第j个输出控制增量的加权因子,数值越大表示重要性比重越大,结果期望动作变化越小。在本方法中γy的选取尤其重要,基于αβ的协调控制中首先是各自的大小其次是二者的相近程度,因为当二者完全一致的时候轮毂碾压面基最小最有利于作物生长,其次是速度,速度和角度共同决定了车辆的行驶状态。
umin是电机的启动电压,umax是电机的最高承受电压,δumin和δumax是电压值的最小最大变化量,ymin和ymax是车辆姿态转角和车辆速度的最大最小值,r(k+1)表示给定的参考序列,表示为:
(2)将约束mpc优化问题改写为如下精简形式:
s.t.lmin≤gz≤lmax(30)
其中各个矩阵为:
w=2(sutγytγysu+γutγu),c=-2sutγytγyep(k+1|k),
矩阵c中的ep(k+1|k)为:
ep(k+1|k)=r(k+1)-yp(k+1|k)(30)
矩阵δumin,δumax,ymin(k+1)和ymax(k+1)如下:
只需求解以上二次规划问题即可得到最优控制序列δu(k)。只需要选取正定的γyγu那么矩阵w就是正定的同时待优化目标函数就是严格凸的并且线性约数的可行域是凸集,所以上述二次规划问题的解就满足karush-kuhn-tucker(kkt)最优条件,求解这个方程获得当前时刻最优解控制序列。
步骤8:如图5所示流程将步骤7得到的预测最优解的第一组时序应用到控制时序,同时对步骤3中线性化后的矩阵进行更新迭代,更新由此而带来随后的二次型的矩阵。
- 还没有人留言评论。精彩留言会获得点赞!