一种三维激光雷达与双目可见光传感器的融合标定方法与流程

本发明涉及自动驾驶的环境感知技术领域，具体为三维激光雷达与双目可见光传感器的融合标定方法。

背景技术：

自动驾驶系统中最基本的问题是感知，通过各类车载传感器，实现对环境的建模、系统自身的定位以及目标检测与识别。

激光雷达是以激光为光源进行测距的传感器，它通过向周围发射激光，然后根据发射到接收的时间间隔确定物体的距离。然后，根据距离及激光束的角度，计算出物体的位置。激光雷达的激光波长一般在600nm～1000nm，所以激光雷达的测距精度很高。目前的车载激光雷达对道路场景下的车辆等目标的检测距离可达到200米以上，具备较远距离的探测能力。这些优点使得激光雷达常被用做无人系统的主传感器。

可见光传感器的成本低廉、采集的环境信息丰富、对近距离的物体检测精度很高，可见光图像提供了物体的颜色、纹理及光谱等关键特征，易于进行物体识别、跟踪。但是，二维图像容易受到环境光照变化影响(如天气变化、光源朝向、夜间错车等因素)。此外，二维图像不包含深度信息。因此，基于二维图像数据的场景理解稳健性差，且难以精确地提取目标轮廓、空间位置等关键信息。

与双目测距相比，激光雷达测距精度更高，但存在扫描频率较低、点云稀疏、缺少纹理信息等缺点；而双目测距可以获取稠密点云，但其依赖于立体匹配的准确性，测距误差较大。实际驾驶环境为典型的非结构化道路场景，并且存在大量交通标志物、障碍物等，仅靠单一的传感器难以获得好的感知效果，将三维激光雷达和二维可见光图像进行融合，可以得到大尺度场景的几何结构信息和场景的色彩信息，获得精度较高、信息丰富、场景多元化的建模效果，以更好地实现复杂环境三维建模与目标识别。

激光雷达和双目可见光传感器的精确标定，包括激光雷达标定、双目相机标定以及激光雷达和双目相机的联合标定，是实现不同坐标系数据关联的前提。激光雷达在出厂时已经过了标定、校准处理，用户一般不需要再进行标定。相机的标定，是为了获得相机的内在参数与畸变参数。双目相机的标定，还需要获取两个相机坐标系之间的旋转矩阵、平移向量，以便后续进行双目测距。激光雷达和相机的联合标定是为了获得激光雷达坐标系与相机坐标系之间的6自由度运动参数，即旋转矩阵、平移向量。

现有的激光雷达与可见光传感器的融合标定方法，通常利用两传感器获取标定板的平面方程，然后采用非线性优化的方法，最小化方程参数的重投影误差。这类方法需要采集多组数据，以便非线性优化的迭代计算，标定过程较为复杂。

技术实现要素：

本发明提出了一种三维激光雷达与双目可见光传感器的融合标定方法，能够精确地对三维激光雷达与双目可见光传感器进行融合标定，获取二者坐标系的旋转矩阵与平移向量，以便进行三维点云与二维可见光图像的数据融合。

本发明的关键是利用激光雷达与双目可见光传感器获取标定板平面顶点的三维坐标，然后对其进行配准，以获得二者坐标系的转换关系，具体步骤如下：

1.搭建融合标定系统，包括三维激光雷达、双目相机与棋盘格标定板，标定板平面为正方形；

2.双目相机的立体标定；

3.双目相机获取标定板顶点的三维坐标；

4.激光雷达获取标定板顶点的三维坐标；

5.将双目相机与激光雷达分别获取的标定板顶点，采用迭代最近点(icp)算法进行配准，得到两传感器坐标系之间的旋转矩阵、平移向量。

附图说明：

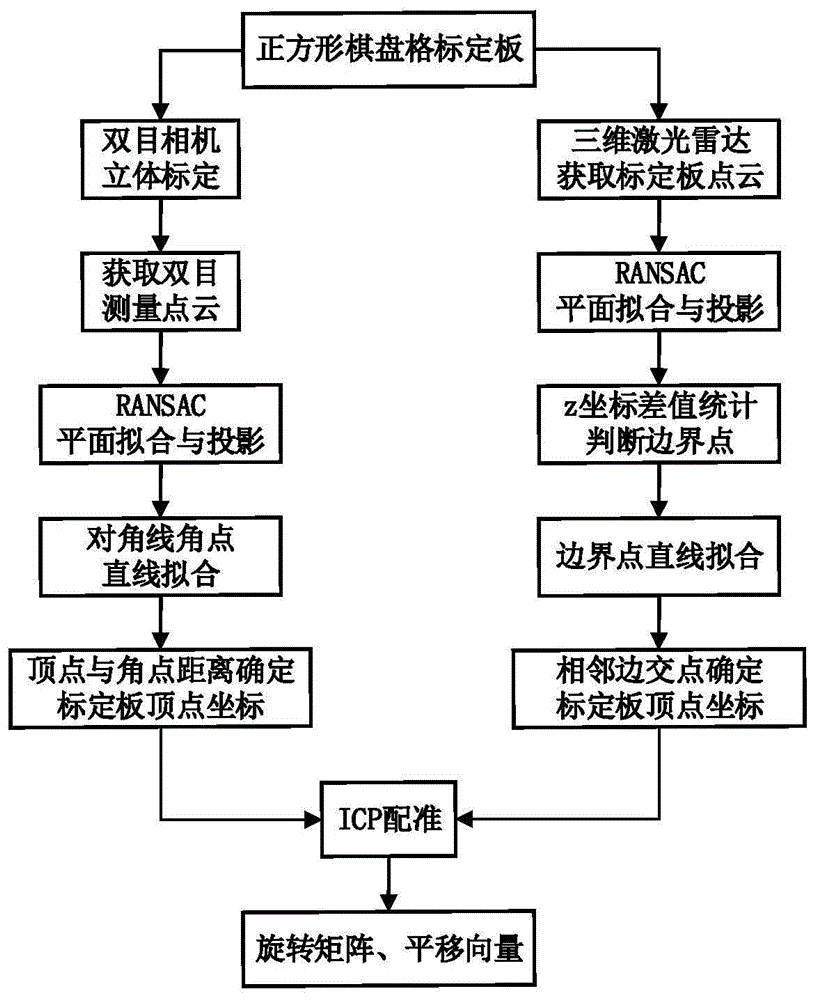
图1：系统流程图

图2：标定板

图3：双目相机获取的标定板点云及顶点

图4：激光雷达获取的标定板点云及顶点

图5：点云配准结果

具体实施方式：

本发明的系统流程图如图1所示，具体实施步骤如下：

1.搭建融合标定系统，包括三维激光雷达、双目相机与棋盘格标定板，标定板为贴有棋盘格图案的不透明亚克力板，标定过程中，将标定板的一个顶点作为悬挂点，则两条对角线分别与地面垂直和平行，调节标定板高度使其四条边都与激光雷达的扫描线相交。

2.双目相机的立体标定

首先对左右两个相机分别进行单目相机标定，采用棋盘格标定板以及张正友标定法，改变标定板的位置、角度，采集多组数据，获取左右相机的内参矩阵、畸变系数，以及每组数据中左、右相机各自的旋转矩阵rl、rr与平移向量tl、tr，下角标l、r分别表示左、右相机。然后对左右两个相机进行立体标定，根据t＝tr-rtl，可以得到两个相机坐标系之间的旋转矩阵r、平移向量t，将多组数据得到结果进行平均作为初始值，采用levenberg-marquardt算法，最小化棋盘格角点在两相机中的重投影误差，得到最优化的r、t。

3.双目相机获取标定板顶点的三维坐标

根据立体标定的结果，对双目图像进行立体校正，利用三角测量的原理，可以获得棋盘格角点的深度信息：

其中，fx为x方向的像素焦距，tx为双目相机的基线长度，即平移向量t的x维的值；d为双目图像中匹配点的像素视差。

然后，根据相机的内参矩阵，可以得到其三维坐标：

采用随机抽样一致性(ransac)算法，对标定板点云进行平面拟合。ransac算法的步骤如下：

1)从样本点集中随机选取一个样本子集，使用最小方差估计对该子集计算三维平面模型参数；

2)然后计算所有样本与该模型的偏差，与预设的阈值进行比较，当偏差小于阈值，该样本点属于内点，否则属于外点，记录当前的内点数目；

3)重复上述步骤，将内点数最多的模型作为最佳模型；

4)每次迭代的末尾，根据期望的误差率、当前迭代次数等，判断是否结束迭代。

采用ransac算法可以剔除噪声等因素产生的外点的影响，得到全局最优的参数估计。

拟合得到标定板平面方程后，将所有角点投影到拟合平面上。

然后，在拟合平面上，提取标定板对角线上的角点，采用最小二乘法分别进行直线拟合，得到标定板两条对角线的三维直线方程。假设某三维直线的方程为如下形式：

该直线上的一系列点为{(x1,y1,z1),(x2,y2,z2),...(xn,yn,zn)}，将其带入直线方程可得：

然后可通过svd求该方程的最小二乘解，即得到待拟合直线的参数。

标定板的四个顶点分别位于两条对角线上，根据各顶点与其最近角点的距离以及三维直线方程，求解得到四个顶点的三维坐标。

4.激光雷达获取标定板顶点的三维坐标

从激光点云中分割出标定板的点云，采用ransac算法，对标定板点云进行平面拟合，并将标定板的点云投影到拟合平面上，投影后的标定板点云可用下式计算相邻点的距离差值：

di＝||pi+1-pi||(6)

其中，pi与pi+1分别为第i个点与第i+1个点的三维坐标，||||为计算二范数。

对得到的相邻点的距离差值进行统计得到均值μ与标准差σ，并以μ+kσ为阈值，大于阈值的点，判断为标定板的边界点，k的取值范围为3～6。

利用提取的四条边的边界点，采用最小二乘法分别进行直线拟合，得到标定板四条边的三维直线方程，分别求解相邻边的交点，得到标定板的四个顶点的三维坐标。

5.将双目相机与激光雷达分别获取的标定板顶点，采用迭代最近点(icp)算法进行配准，得到两传感器坐标系之间的旋转矩阵、平移向量。假设通过一次或多次测量得到的标定板顶点匹配点集分别为：

则匹配的目的是求解一个欧氏变换r,t，使得：

首先构建一个最小二乘问题，求解使得误差平方和最小的r,t：

计算两组点集的质心：

经推导，优化目标函数可简化为：

其中，为去质心坐标。则icp算法可以分为三个步骤：

1)计算两组点集的质心，并计算其去质心坐标；

2)根据以下优化问题计算旋转矩阵：

3)根据2)所得的r计算t：

t＝pc-rpl(15)

步骤2)是一个典型的优化问题，可以通过svd求解，定义矩阵：

w是一个3×3的矩阵，对其进行svd分解，得：

w＝uσv^t(17)

则，旋转矩阵为：

r＝uv^t(18)

为验证上述三维激光雷达与双目可见光传感器的融合标定方法，进行验证实验。实验中采用的标定板如图2所示，为80cm×80cm×3mm的不透明亚克力板，棋盘格图案为12×12个大小为6cm×6cm的黑白方块，标定板中包含了11×11个角点，棋盘格图案四条边界距离标定板边界都为4cm；双目相机为小觅双目摄像头mynteyed1200；激光雷达为八线三维激光雷达quanergym8。

采用双目相机获取的标定板顶点如图3所示；采用激光雷达获取的标定板顶点如图4所示。利用二者获取的顶点进行icp配准，标定结果如下：

t＝[-0.184988-0.2390180.129789]^t(20)

根据标定结果，将激光雷达的标定板点云转换到双目相机坐标系，如图5所示。