一种应用于隧道初期结构设计的直接弹性抗力法的制作方法

本发明属于隧道(洞)施工技术领域，具体涉及一种应用于隧道初期结构设计的直接弹性抗力法。

背景技术：

所有隧道施工人员(管理、技术、隧道工)心中始终存有一个疑问——在没有施作二次衬砌前由喷锚等材料构成的隧道初期支护足够安全吗？之所以有这样的疑问是有着客观原因的。《铁路隧道设计规范》tb10003-2016之“8.1.7喷锚衬砌和复合式衬砌的初期支护，可按工程类比法确定设计参数；施工期间应通过监控量测进行修正对地质复杂、大跨度、多线和有特殊要求的隧道，除采用工程类比法外，还应结合数值解法或近似解法进行分析确定”。

“按工程类比法”设计，大家看到的效果是有成功，有失败。最近十几年对工程质量、安全的管理力度不断加强，工程事故率大幅下降，但是隧道坍塌的事故仍然时有发生，尽管这种事故率已经很低，但是也足以动摇人们对隧道未衬砌之前的初期支护的安全信心，施工现场的上下各级管理人员乃至隧道工人都强调“快衬砌”的隧道施工方针就是最典型、最直接的证明。

“结合数值解法或近似解法进行分析确定”，尽管结构进行了详细的计算，但是仍然对结论半信半疑甚至完全怀疑，这是因为所谓的计算模型与现场的施工工序严重不符。几乎所有的隧道力学教材讲的隧道结构计算都是指隧道二次衬砌的计算，并没有明确的初期支护结构计算；有的隧道结构计算是将初期支护和二次衬砌合在一起计算。而初期支护与二次衬砌实际上是按照前后工序分别施工的两种结构，其力学状态完全不同。《铁路隧道设计规范》tb10003-2016之“8.1.10计算有仰拱的隧道和明洞衬砌，当仰拱先施作时，应考虑仰拱对结构内力的影响；当仰拱在边墙之后施作时，则可不考虑仰拱的作用”。隧道初期支护是由上而下施工的，仰拱最后施工，其力学模型不应考虑仰拱的影响，但是二次衬砌是由下而上施工的，仰拱先作，所以其力学模型应考虑仰拱的影响。通常情况下，在距离掌子面2b～2.5b(b为隧道开挖宽度)以外，隧道“空间效应”完全消失，隧道松散荷载也即形成，而隧道二次衬砌距离此处至少有30m的距离，所以在这30m距离内，隧道全部设计荷载是由初期支护单独承受的，二次衬砌尚无法发挥作用。所以将初期支护与二次衬砌合在一起计算的模型与现场严重不符，自然计算结果对现场的指导意义就不足。《公路隧道设计规范》jtg3307.1-2018术语与符号一章甚至没有“初期支护”的概念，这就更加重了人们对隧道初期作用原理以及其安全性的疑虑。

《铁路隧道设计规范》tb10003-2016之“8.1.9隧道衬砌宜采用荷载-结构模型进行计算”，当前流行的隧道衬砌结构力学计算方法有不考虑地层影响和考虑地层影响(弹性抗力)两种方法，其中考虑地层弹性抗力影响的主要是布加耶娃假定抗力法,诸多文献按照此法来计算隧道二次衬砌的，逻辑上讲是可以计算隧道初期支护结构的，但是，若用此法来计算隧道初期支护结构，就会得出隧道初期支护结构无法单独承载的结论(按照有关规范确定的参数)，这显然与事实不符，这就说明“假定抗力法”中的“假定”与实际相差太远。急需寻找一种更贴近实际且计算简便的方法来解释隧道初期支护承载能力。

技术实现要素：

为了克服上述现有技术的不足，本发明的目的是提供一种应用于隧道初期结构设计的直接弹性抗力法，隧道初期支护结构在垂直和水平荷载作用下，拱部会产生不受围岩约束的负位移脱离区(向着隧道断面轮廓圆心)，侧部产生受到围岩约束的正位移，两部结构因地基弹性抗力有无的差别，拱部结构的内力及位移用普通拱函数来表示，侧部结构的内力及位移用弹性地基拱函数来表示。

为了实现上述目的，本发明采用的技术方案是：

1、一种应用于隧道初期结构设计的直接弹性抗力法，基本原理如下：

隧道初期支护结构在垂直和水平荷载作用下，拱部会产生不受围岩约束的负位移脱离区，即向着隧道断面轮廓圆心的位移，侧部产生受到围岩约束的正位移。拱部产生负位移的结构的内力及位移用普通拱函数来表示，侧部产生正位移的结构的内力及位移用弹性地基拱函数来表示。

2、其计算包括以下步骤：

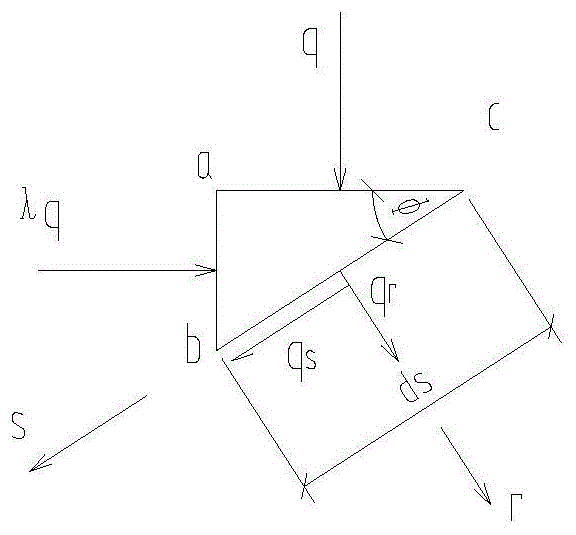
步骤1、将直角坐标系中的荷载的型式转化为极坐标型式，荷载转化后的函数式为：

式中：q为垂直荷载，λ为侧压力系数，qr为法向荷载，qs为切向荷载，为计算点位与隧道中心线的夹角。

步骤2、确定拱与弹性地基拱的分界点：先按照不考虑弹性抗力计算结构的弯矩及位移，见以下公式：

式中：m为结构弯矩，u为结构位移，r为拱结构半径(拱弯曲前后计算半径认为不变)，e为结构弹性模量，i为结构截面惯性矩，其余符号意义同上。

直接弹性抗力法计算模型为两铰拱，由于弯矩和位移的0点位置不受荷载及材料影响，因此可以推断在施加弹性抗力后，弯矩及位移0点位置仍然不变，而拱与弹性地基拱的分界点即为两铰拱位移0点，公式(4)中，令u＝0时，得：

步骤3、拱的弯矩、轴力、位移微分方程及其函数表达式为：

式中参数c0、c1、c2由拱两端的力和位移条件确定。

步骤4、弹性地基拱的弯矩、轴力、位移微分方程及其函数表达式为：

求解式(12)，并令(式中k为围岩弹性抗力系数)，并考虑对称性，可得：

式中参数a0、a1、a2由拱两端的力和位移条件确定；

步骤5、拱与弹性地基拱的弯矩、位移函数参数的求解：设拱的弯矩和位移分别为m1、u1，弹性地基拱的弯矩和位移分别为m2、u2；

将u2＝0；u2＝0、m2＝0，带入公式(13)、(14)，得到参数a0、a1、a2，得m2、u2。

由u1＝0、m1＝m2、

求得参数c0、c1、c2，得m1、u1。即得到支护结构的全部弯矩、位移，并由相应的应力平衡条件得到结构的轴力，因此可得出结构的截面应力，进行结构的设计。

本发明的有益效果是：

1、直接弹性抗力法是相对于假定弹性抗力法的，其隧道支护结构的弹性抗力与结构位移是同步计算的，更加真实地反映了支护结构的应力状态；由此原理，按照当前流行的隧道支护结构设计参数，可得出隧道支护结构具有约3倍的安全系数，这样就可以彻底消除人们对支护结构能否单独承载的疑虑，因此产生的效果如执行“快衬砌”方针而造成衬砌开裂的事件可以避免，及采取cd法、crd法、双侧壁导坑法开挖等严重制约工程进度的工法等都可得以解决。

2、支护结构内力(弯矩和轴力)、位移函数中的未知参数(两段函数共六个参数)仅需三个边界条件即可一次确定弯矩、轴力、位移函数，计算更加简便。

附图说明

图1为荷载型式转化图；

图2拱的微段内力平衡图；

图3拱的正应力公式导出图；

图4是设ab＇是拱变形后的曲线图；

图5是图4中的ε0用m-n轴上各点位移来表示的示意图；

图6为弹性地基拱的微段内力平衡图；

图7为接弹性抗力法两铰拱模型计算模型图；

图8为支护结构位移图；

图9为支护结构弯矩图；

图10为支护结构轴力图。

具体实施方式

以下结合附图对本发明进一步叙述。

1、直接弹性抗力法基本原理

隧道初期支护结构在垂直和水平荷载作用下，拱部会产生不受围岩约束的负位移脱离区(向着隧道断面轮廓圆心)，侧部产生受到围岩约束的正位移。故拱部结构的内力及位移用普通拱函数来表示，侧部结构的内力及位移用弹性地基拱函数来表示。

2、荷载的直角坐标转化为极坐标型式

在隧道支护结构边缘取一三角形微分单元体，如图1。

根据平衡条件，可求得：

3、拱的内力及位移函数

3.1拱的内力和平衡方程

用相距为ds的截面mn和m＇n＇从拱中截取一个微段(见图2)，若将微段上的所有力投影于m＇n＇截面上的s轴和r轴，并对m＇n＇截面的z轴(垂直于纸面)取矩，由平衡条件得。

注意到在以上平衡方程中：

略去二阶微量，得。

3.2拱的截面正应力公式

从拱结构中截取微段，其左右两侧去掉部分对微段的影响以作用力代替(如图3)。

设此作用力简化为轴力n和弯矩m。所有力在x轴(梁轴切线)上的投影

ν＝∫fσ·df(9)

绕z轴(垂直纸面)的力矩和

m＝∫fσ·y·df(10)

且设定

∫fσ·z·df＝0

图中：r—拱弯曲前的曲率半径；dφ—为相邻断面间原来的夹角；ds—梁微段轴线处纤维长度；dsy—距离断面重心为y的梁的纤维长度。

根据平面断面假定，在断面中心轴力n作用下，断面平面ab(图3)移到a＇b＇,微段轴线曲率没有发生变化；再在弯矩m作用下断面发生旋转，最终平面ab移到a＂b＂。

纤维长度dsy的增量

略去梁横向变形，即，令δy＝0，最后得到：

纤维的相对伸长：

注意到得到：

设则式(11)为：

由胡克定律：

将(13)代入(9)、(10)，得：

式中f＝∫fdf是梁横截面面积。

式中：

由(15)得：

由(14)、(15)得：

代入(13)式，得：

由于r≥y，故就变为i＝∫fy²df(下文中i′均以i代替)，因此有：

3.3拱的弯曲位移微分方程

设ab＇是拱变形后的曲线(图4)，

由得：

由(17)得：

代入上式，得

现在将(21)中的ε0用m-n轴上各点位移来表示(图5)。

拱的法向位移为u，切向位移为υ。由于拱的位移几乎为纯弯曲，纤维的伸长很小，剪力的影响也极小，故忽略切向位移υ。

法向位移引起的相对伸长ε0可表示为：

由图(图5)看到，由法向位移引起的m点切线倾角改变为n点的角度改变为：

因此m、n点间角度的增量为：

将求得的ε0代入(21)式，得拱的位移微分方程为：

3.4拱的弯矩、位移微分方程及其函数表达式

由(1)、(2)、(6)、(7)、(8)、(22)式可得：

求解(25)，并考虑对称称性，可得：

式中参数c0、c1、c2由拱两端的力和位移条件确定。

4弹性地基拱的内力平衡方程

4.1弹性地基拱的内力及平衡方程

用相距为ds的截面mn和m＇n＇从弹性地基拱中截取一个微段(见图6)，若将微段上的所有力投影于m＇n＇截面上的s轴和r轴，并对m＇n＇截面的z轴(垂直于纸面)取矩，由平衡条件得。

注意到在以上平衡方程中：

略去二阶微量，得。

4.2弹性地基拱的弯矩、位移微分方程及其函数表达式

由(1)、(2)、(31)、(32)、(33)、(22)式可得：

求解式(12)，并令(式中k为围岩弹性抗力系数)，并考虑对称性，可得：

式中参数a0、a1、a2由拱两端的力和位移条件确定。

5直接弹性抗力法计算隧道初期支护

以两铰拱模型为计算模型(图7)。

本计算所用到的参数：

r＝7.2m，q＝280kn/m²,侧压力系数λ＝0.5，初期支护厚0.28m，ⅴ级围岩，弹性反力系数k＝0.1×10⁶kpa/m,混凝土弹性模量ec＝2.3×10⁷kpa。

5.1拱与弹性地基拱的分界点确定

先按照不考虑弹性抗力计算结构的弯矩及位移。

由以上二式可知，弯矩和位移的0点位置不受荷载及材料影响，因此可以推断在施加弹性抗力后，弯矩及位移0点位置仍然不变。而拱与弹性地基拱的分界点即为两铰拱位移0点。

由(40)令u＝0，解得:

5.2设拱的弯矩和位移分别为m1、u1，弹性地基拱的弯矩和位移分别为m2、u2。

由：u2＝0；u2＝0、m2＝0代入(37)、(38)式，求得参数a0、a1、a2，得m2、u2。

a0＝-0.9238957639×10^-4

a1＝-1.269231897×10^-9

a2＝-1.086512112×10^-9

由：u1＝0、m1＝m2、

求得参数c0、c1、c2，得m1、u1。

c0＝5.063238328

c1＝-4.330343707

c2＝-3.603654375

得直接弹性抗力法计算的结构位移、弯矩、轴力如图8、图9、图10。