电磁场有限元快速频率分析的电磁灵敏度分析方法

1.本发明涉及计算电磁学中的有限元分析法，具体涉及一种电磁场有限元快速频率分析的电磁灵敏度分析方法。


背景技术：

2.电磁灵敏度是电磁响应对几何或材料参数的导数。电磁场灵敏度(导数)分析对基于电磁的设计至关重要。基于电磁场灵敏度进行电磁场的设计，如设计优化、分析和成品率设计等等，可以大幅提升电磁场设计效率。伴随变量法被认为是进行电磁场灵敏度(导数)分析最有效的方法。然而目前的电磁灵敏度分析技术是频率相关的，必须针对不同的频率重复求解大规模系统的电磁方程，所以现有的电磁灵敏度分析方法在频率数目较大时非常耗时。
3.模型降阶技术可以有效解决电磁场仿真中重复求解大型的电磁方程组的难题，使用模型降阶技术，电磁方程只需在单一频率下求解，其他频率的解可以用很小的计算开销来近似。常用的模型降阶技术包括asymptoticwaveformevaluation(awe)方法、galerkin awe(gawe)方法、well
‑
conditioned awe(wcawe)方法、arnoldi方法、pad
é
via lanczos(pvl)方法、matrix pad
é
via lanczos(mpvl)方法、adaptive lanczos
‑
pad
é
sweep(alps)方法等等。使用模型降阶技术对电磁问题进行快速频率分析，可以避免对不同频率的大型线性系统进行重复求解，从而加快电磁仿真的速度。然而该方法不能直接用于电磁场灵敏度(导数)分析问题的加速，为了进一步加快设计优化，需要对如何使用模型降阶技术进行快速电磁灵敏度分析进行研究。


技术实现要素：

4.本发明目的是提出一种电磁场有限元快速频率分析的电磁灵敏度分析方法。该方法通过仅在单个频率上求解电磁场灵敏度方程，获得了整个频带的精确电磁场灵敏度，推导了基于有限元的模型降阶技术的伴随/自伴随公式，进一步加快了电磁灵敏度分析的速度。
5.为实现本发明的目的，本发明的技术方案如下：
6.一种电磁场有限元快速频率分析的电磁灵敏度分析方法，包括如下步骤：
7.步骤1：电磁场分析中mpvl算法的单倍大小简化步骤；
8.步骤2：使用快速频率分析的伴随电磁灵敏度分析步骤。
9.与现有技术相比，本发明提出了电磁场有限元快速全频域分析(fast frequency sweep)的伴随电磁导数求解方法。国际流行电磁商用软件目前仍使用逐一频率电磁导数求解方法，导数求解效率低，本发明所提出的方法将模型降阶算法引入求解伴随电磁导数，求解速度大幅提升，且所需求解频率越多速度提升越显著(如求解100个频率，求解速度提升高达30倍)。
10.具体包括如下三种创新：
11.1.em分析中mpvl算法的单倍大小简化：传统的mpvl算法需要求解双倍大小矩阵，该方法所提技术可以使用单倍大小的矩阵进行mpvl算法的简化改进；
12.2.使用快速频率分析的伴随电磁灵敏度分析：快速全频域分析的伴随电磁导数求解的简化方法，相比于离散求解效率提高显著；
13.3.使用快速频率分析的自伴随电磁灵敏度分析：快速全频域分析的自伴随电磁导数求解的简化方法，相比于伴随电磁灵敏度分析方法求解效率进一步提高。
附图说明
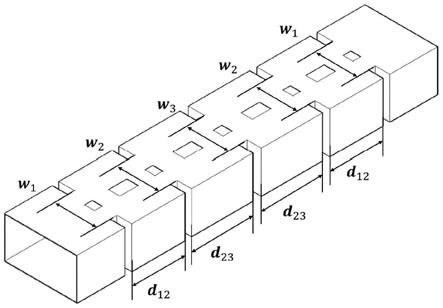
14.图1：四极波导滤波器的结构第一示意图。
15.图2：四极波导滤波器的结构第二示意图。
16.图3：四极波导滤波器的扫频范围为10.5ghz
‑
11.5ghz时，res
11
和ims
11
对h1在φ1处的导数。
17.图4：四极波导滤波器的扫频范围为10.5ghz
‑
11.5ghz时，res
21
和ims
21
对h1在φ1处的导数。
18.图5：四极波导滤波器的扫频范围为10.5ghz
‑
11.5ghz时，res
11
和ims
11
对h
c2
在φ1处的导数。
19.图6：四极波导滤波器的扫频范围为10.5ghz
‑
11.5ghz时，res
21
和ims
21
对h
c2
在φ1处的导数。
具体实施方式
20.需要说明的是，在不冲突的情况下，本技术中的实施例及实施例中的特征可以相互组合。
21.以下结合附图和具体实施例对本发明作进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。
22.本发明将模型降阶算法的一种，即mpvl方法，引入电磁场灵敏度分析中，电磁场灵敏度方程只需在单一频率下求解，其他频率的解可以用很小的计算开销来近似，从而加快整个频带的电磁灵敏度分析。在本发明中，推导了基于单频有限元的伴随/自伴随公式，用于预测整个频带的电磁灵敏度信息，采用该方法进行的电磁灵敏度分析可以获得与现有方法相同的精度，同时避免了对不同频率的大型电磁方程组的重复求解，从而节省了时间。试验结果表明，使用所提出的技术进行的电磁灵敏度分析获得了与现有技术相同的精度，同时通过避免重复求解不同频率的大型电磁方程组，花费更少的时间。
23.本发明的技术方案，首先阐述了电磁场仿真的有限元求解方法，发明了电磁场分析中模型降阶算法中mpvl算法的单倍大小简化方法。在此基础上开发了适用于电磁场灵敏度(导数)的新型模型降阶算法，提出了使用快速频率分析的伴随电磁灵敏度分析方法，大幅加速了电磁灵敏度分析。在上述发明基础上引入自伴随的概念，进一步提出了快速频率分析的自伴随电磁灵敏度分析，进一步加速了电磁灵敏度分析。
24.下面对本发明的技术方案做详细阐释：
25.一、电磁场分析中mpvl算法的单倍大小简化
26.全波电磁模拟的亥姆霍兹方程为：
[0027][0028]
其中，∈和μ分别表示介质的介电常数和磁导率；ω表示角频率；j表示电磁问题的电流源；e表示需要求解的电场强度。有限元法是求解这一亥姆霍兹方程的常用方法之一。假设电磁仿真是在一个多端口结构上执行。求解电磁场问题的有限元方程可概括为：
[0029]
(k0+sk1+s2k2)x＝sb
j
，
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(2)
[0030]
其中，s表示对应ω的复频率；x表示未知场解向量，包含有限元求解的未知电场；k0，k1，k2表示全局有限元系统矩阵，它依赖于设计变量，但独立于s；b
i
表示一个第j个端口的电磁激励。为了得到多端口结构的全散射矩阵，s参数可以定义为：
[0031][0032]
其中，
[0033][0034]
其中，κ
k，j
是一个常数，它取决于第i和第j个端口的功率输入。
[0035]
让n被定义为x中元素的个数。该方法采用mpvl方法进行基于有限元的快速频率分析。mpvl的有限元方程必须只包含一阶频率s项。为了将mpvl应用于有限元矩阵系统，需要将(3)重新转化为，
[0036][0037]
其中
[0038][0039]
其中i
n
和o
n
分别表示单位矩阵和零矩阵中的
[0040]
让φ表示设计参数向量。让φ
i
代表了第i个元素φ，i＝1，...，p，在那里p为设计参数的总数。
[0041]
为了使用mpvl算法进行快速频率分析，选择一个特定的频率并定义为求解频率。通过选择合适的解频率，可以在解频率处一次性求解大型线性系统，得到整个频带的精确解。让s0表示mpvl的求解频率。让a
s
是一个2n
×
2n矩阵(两倍大小的系统矩阵)，定义为：
[0042]
[0043]
其中a
s
是在解频率s0处计算的。让q为mpvl简化模型的阶数。让定义为含元素t
l，m
，即，的降阶矩阵，其中l＝1，2，...，q和m＝1，2，...，q。让定义为一组相互正交的单位向量。让定义为包含模型降阶krylov子空间的标准正交基的矩阵，其中让r
m
定义在第m次mpvl迭代中计算和的向量。r
m
是通过求解线性方程组来计算的：
[0044][0045]
采用mpvl作为模型降阶技术进行快速频率分析，需要计算lu因子矩阵a
s
。让k
s
代表求解频率下n
×
n的有限元系统矩阵(单倍大小系统矩阵)，表示为：
[0046][0047]
因为a
s
是原来有限元系统矩阵k
s
的2倍，lu因子分解a
s
的计算代价花费的时间比原来的系统矩阵k
s
长得多。
[0048]
本技术推导了一个更紧凑的mpvl算法来执行原系统k
s
的lu分解(单倍大小系统矩阵)而不是a
s
(两倍大小系统矩阵)。利用分块矩阵的求逆算法，将(8)重新表述为：
[0049][0050]
和
[0051][0052]
让u
m
定义为线性方程组的解向量，
[0053][0054]
将(12)代入(10)和(11)，可以得到
[0055][0056]
和
[0057][0058]
其中，m表示mpvl迭代索引，即m＝1，2，...，q.让代表q阶降阶向量(q
×
1向量)，推导为：
[0059][0060]
其中，是中第一个单位向量；i
q
是中一个单位矩阵。
[0061]
将(15)代入(5)，可以得到单倍大小mpvl算法的s参数计算公式，公式为
[0062][0063]
用于电磁分析的mpvl算法的单倍大小简化的详细信息总结在下述算法1。
[0064]
[0065][0066]
二、使用快速频率分析的伴随电磁灵敏度分析
[0067]
让和分别表示g和c关于几何设计变量φ
i
的导数。和可以推导为
[0068][0069]
其中分别表示k0，k1，k2关于几何设计变量φ
i
的灵敏度。为了计算灵敏度s
i，j
，全局灵敏度有限元系统矩阵等设计参数需要首先获得。
[0070]
向量b
j
的边界条件和(或)电磁激励从第j个端口获得。在电磁设计过程中，端口的结构一般不会发生变化。因此在电磁问题中，
ꢀꢀ
b
j
是对于设计变量φ
i
等的常数向量，即，
[0071]
[0072]
由(5)得到s
k，j
的导数，
[0073][0074]
让x
j
表示线性方程组的解向量，
[0075]
(g+sc)x
j
＝β
j
.
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(20)
[0076]
解向量x
j
在(20)中可以通过模型降阶技术计算，如mpvl算法。
[0077]
让定义为伴随线性系统的伴随解向量，
[0078][0079]
解向量在(11)中可以通过模型降阶技术类似的计算x
j
，如mpvl算法。将(20)和(21)代入(19)，得到s
k，j
关于φ
i
伴随灵敏度公式为，
[0080][0081]
方程(22)是适用于快速扫频的伴随灵敏度公式。模型降阶技术可以用于计算x
j
和由于(22)的形式是使用mpvl推导的，x
j
和可以用mpvl算法来表示。至此本技术推到出了一个可以直接适用于mpvl方法的电磁场灵敏度求解公式，将mpvl方法带入可以得出基于mpvl的伴随电磁场灵敏度求解公式：
[0082][0083]
算法2中总结了本发明的使用mpvl的伴随电磁场灵敏度算法。
[0084]
[0085]
[0086][0087]
三、使用快速频率分析的自伴随电磁灵敏度分析
[0088]
本发明进一步提出了一种自伴随电磁灵敏度分析。因为g和c被制定为2
×
2分块矩阵，将(6)代入(20)，并使用2
×
2分块矩阵的求逆算法，可以得到
[0089][0090]
其中
[0091]
k＝k0+sk1+s2k2.
ꢀꢀꢀ
(25)
[0092]
因为k0，k1，k2是对称矩阵，通过将(6)代入(21)并使用2
×
2分块矩阵的求逆算法，可以得到，
[0093][0094]
让ξ
k
定义为和x
k
的向量权重差，
[0095][0096]
这样可以用x
k
和ξ
k
的加权求和来表示，
[0097][0098]
将(17)代入(22)可得
[0099][0100]
因为
[0101]
[0102]
计算导数的公式(29)可进一步简化为：
[0103][0104]
式(31)为自伴随灵敏度公式，非常适合于快速扫频。更多的技术可以用于计算x
j
.由于(31)的格式是使用mpvl派生的，x
j
可以用mpvl算法来表示。
[0105]
利用公式(12)
‑
(14)，本技术对原有限元系统矩阵k
s
进行lu因子分解和正向/反向替换(单倍大小系统矩阵)而不是a
s
(两倍大小系统矩阵)，从而减少计算时间r
m
，m＝0，1，...，q.因为mpvl的主要计算时间是计算r
m
，所以x
k
采用紧凑的mpvl算法可减少总的计算时间。注意，根据(12)
‑
(14)，k
s
的lu因子只需要计算一次，而mpvl算法需要进行q+1次前向和后向替换。
[0106]
由于(31)的形式是使用mpvl推导的，x
j
和x
k
可以用mpvl算法来表示，且求解方法相同。至此本技术推到出了一个可以直接适用于mpvl方法的自伴随电磁场灵敏度求解公式，将mpvl方法带入可以得出基于mpvl的自伴随电磁场灵敏度求解公式：
[0107][0108]
算法3中总结了本发明的使用mpvl的自灵敏度算法的细节。注意，在算法1需要适当的被选择来使每一个λ
m
为非零。利用所提出的自伴随灵敏度分析公式(32)，可以在mpvl算法进行快速频率分析时有效地计算s参数关于设计变量的导数。使用带有q阶简化模型的快速频率分析来评估关于一个p端口结构设计参数的s参数及其导数，只有一个lu的因式和p(q+1)次向前/向后替换需要执行。使用所提出的自伴随灵敏度分析技术的计算时间与设计变量的数量无关，并随频率的增加略有增加。
[0109]
[0110][0111]
下述表1比较了不同算法的灵敏度分析。表1比较了本发明使用快速频率扫描的伴随灵敏度分析方法中原始有限元矩阵lu分解的详细数量和f/b替换次数，为了进行比较，我们还展示了使用离散频率扫描的自伴随灵敏度分析的细节，使用有限差分法(即扰动变量，重新模拟电磁并计算解差)进行灵敏度分析，用于快速扫频和离散扫频。出于说明目的，我们还展示了使用快速频率扫描和离散频率扫描的电磁仿真的详细信息。表1中，n表示设计变量的个数；n
f
表示频率数；q代表mpvl的阶数；p代表微波结构的端口数。从表1中，我们可以看到，如果电磁应用程序仅在1或2个频率下进行仿真，我们会使用离散频率扫描的自伴随灵敏度分析来执行灵敏度分析。如果电磁应用只有1或2个设计变量，我们使用有限差分法和快速频率扫描来执行灵敏度分析。如果电磁应用有更多的设计变量并且需要在更多的频率下进行仿真，那么所提出的使用快速扫频的伴随灵敏度分析方法可以比现有的灵敏度分析方法更快地获得结果。电磁应用程序具有的设计变量和频率越多，所提出的方法将越具有显著的优势。
[0112]
表1：不同算法下有限元矩阵lu分解数和f/b替换数的比较
[0113][0114]
n
‑
变量数；
[0115]
n
f
‑
频率数；
[0116]
q
‑
mpvl阶数；
[0117]
p
‑
微波结构的端口数。
[0118]
注：需要注意的是，所提出的自伴随电磁灵敏度算法与有限元法快速扫频电磁仿真采用相同数量的lu分解和f/b替换。换句话说，在使用快速扫频进行电磁仿真后，不需要额外的lu或f/b时间来计算所有变量的电磁灵敏度。电磁仿真后，对电磁灵敏度进行分析只需要少量额外的矩阵乘法时间。
[0119]
四、采用四极波导滤波器的灵敏度分析案例进行有益效果对比说明
[0120]
所考虑的例子是四极波导滤波器的灵敏度分析。调谐元件是位于每个腔体和每个耦合窗口中心的方形截面穿透柱，如图1、图2所示。让h1，h2，h3表示耦合窗口中的调优柱的高度。让h
c1
和h
c2
表示放置在谐振腔中心的正方形截面的高度。让w
c
和w
p
分别表示位于谐振腔中心的方形截面的宽度和耦合窗口的宽度。让d
12
和d
23
表示共振腔的直径。虹膜宽度w1，w2，w3和w4预先调谐以实现滤波器的每个部分所需的耦合带宽。输入和输出波导，以及谐振腔，是标准的wr
‑
75波导(a＝19.05mm和b＝9.525mm)。对于本例，设计空间向量为φ＝[d
12 d
23 h
1 h
2 h
3 h
c1 h
c2 w
1 w
2 w
3 w
p w
c
]
t
.灵敏度分析在公称设计点进行，即：φ1＝[10.5 13.3 3.39 4.15 3.62 3.30 2.98 8.7 5.1 5.1 2.0 4.0]
t
mm，该滤波器的频率范围选择为10.5ghz
‑
11.5ghz，步长为20mhz。
[0121]
设计变量是φ＝[d
12 d
23 h
1 h
2 h
3 h
c1 h
c2 w
1 w
2 w
3 w
p w
c
]
t
[0122]
灵敏度计算采用本发明的自伴随灵敏度分析方法，采用快速频率分析方法对该滤波器进行电磁仿真。降阶模型的阶数为16，即，q＝16。为了比较，我们还使用离散频率分析进行了自伴随灵敏度分析。进一步采用有限差分法对快速频率分析和离散频率分析进行灵敏度分析。对不同频率点个数的灵敏度分析进行三种情况的比较：情况1为11个频率点，情况2为101个频率点。四极波导滤波器实例灵敏度分析的不同算法的比较如表2所示。
[0123]
表2：四极波导滤波器不同灵敏度分析方法的cpu比较
[0124][0125][0126]
由于在本例中使用了12个设计变量，因此在使用有限差分方法进行灵敏度分析时，需要对s参数进行13次完整的评估(1次在标称值和12个不同设计变量的扰动)。对于使用离散频率分析的自伴随灵敏度分析，成本随着电磁设计的频率点数量的增加而增加。从表2中可以看出，所提出的自伴随灵敏度方法仅使用一个lu因子分解和34个正向/反向替换来获得s参数关于12不同的设计参数的导数。lu因子分解和前向/后向替换是整个灵敏度分析过程中最耗时的部分。所提方法所使用的lu因子分解和前向/后向替换的次数远远少于表2中列出的现有方法，因此所提方法所花费的时间远远少于现有方法。
[0127]
图3和图4显示了扫频范围为10.5ghz
‑
11.5ghz的四极波导滤波器的s
11
和s
21
相对于h1的导数的详细比较。如图3和图4所示，所提出的自伴随灵敏度分析方法计算的导数与现有的自伴随方法和有限差分方法计算的导数吻合得很好。为了进一步验证所提出的自伴随灵敏度分析方法的准确性，我们还计算了s参数对其他设计参数的导数。对于这个四极波导滤波器，s
11
和s
21
相对于h
c2
的导数的详细比较分别如图5和图6所示。通过比较，我们可以看到，所提出的自伴随灵敏度分析采用快速频率分析，以非常低的计算代价获得正确的解
决方案。
[0128]
需要说明的是，本技术中未详述的技术方案，采用公知技术。
[0129]
以上所述仅是本发明的优选实施方式，应当指出的是，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。