一种修形人字齿轮成形磨最大砂轮直径精确计算方法与流程

1.本发明涉及的是一种齿轮加工方法，具体地说是齿轮加工参数计算方法。


背景技术：

2.船舶主动力齿轮传动装置多采用人字齿轮，人字齿轮为两个较大螺旋角(一般25
°‑
45
°
)的单斜齿轮组成，这样可以抵消斜齿轮产生的轴向力，在两个单斜齿轮中间留有一定长度的推刀槽，供齿轮加工时刀具的退刀。这种齿轮一般为高精度渗碳淬火硬齿面齿轮，齿轮最后加工工序为磨齿。磨齿方式按照砂轮类型分可分为蝶形双砂轮型、锥面砂轮型、蜗杆砂轮型、成形砂轮型等多种类型，其中成形砂轮型磨齿具有高的加工精度和加工效率，被广泛应用于齿轮磨齿精加工中。影响成形磨齿加工精度的因素有很多，如磨齿机精度、齿面扭曲程度和砂轮等。其中砂轮的最大直径选择是齿轮成形磨中的重要参数，影响着磨齿精度。砂轮直径不易选择过小，因为小砂轮其安装内孔的直径也会较小，这样固定砂轮的砂轮轴的刚性就会较差，从而降低磨削精度。但砂轮直径也不能过大，过大将引起砂轮与退刀槽另一侧轮齿发生干涉现象。目前的工程上成形磨砂轮直径确定多以经验性为主，或者用简单的作图法近似确定，很难适应高精度修形齿轮加工需求。


技术实现要素：

3.本发明的目的在于提供通过建立成型磨削法人字齿轮的双向修形数学模型、根据砂轮磨削的几何条件、计算出砂轮最大直径的一种修形人字齿轮成形磨最大砂轮直径精确计算方法。
4.本发明的目的是这样实现的：
5.本发明一种修形人字齿轮成形磨最大砂轮直径精确计算方法，其特征是：
6.(1)建立齿轮齿廓为三段抛物线修形曲面模型，通过求解渐开线函数得到左、右旋齿轮齿面的位置矢量和法向矢量，进而得到人字齿轮齿面的数学模型；
7.(2)通过工件的位矢、法矢以及砂轮安装参数，推导砂轮与工件的啮合方程，进而得到砂轮与工件接触线方程；并将接触线绕砂轮轴线旋转投影到砂轮截面，得到成形砂轮截面，同时考虑砂轮中心距变动，实现人字齿轮的双向修形；
8.(3)根据砂轮磨削齿面终止点时的几何条件，计算砂轮最大直径。
9.本发明还可以包括：
10.1、步骤(1)具体为：
11.a、根据微分几何齿面共轭理论，确定的齿轮齿面的位置矢量和法向矢量分别为
12.[0013][0014]
式中，rb1为基本半径，μ1为基圆上齿槽宽对所应的半角，θ1为渐开线上点的展开角，螺旋参数p1＝rb1tgλb1，λb1为齿轮基圆上的导程角；上标表示右侧齿面，下标表示左侧齿面，通过上述方法，求得左旋齿轮左、右齿面的位矢和法矢，改变轮齿的旋向，获得人字齿轮另一侧齿面的数学模型；
[0015]
b、在齿轮旋转投影面上，根据几何关系，建立齿廓三段抛物线修形的函数表达式：
[0016][0017]
式中，l1表示齿根修缘长度、l2表示中间鼓形长度、l3表示齿顶修缘长度、a1、a2和a3为第i段抛物线系数、b1为第ii段抛物线系数、c1、c2和c3为第iii段抛物线系数；根据每段抛物线的最大修形量，以及相邻抛物线在连接点的连续相切条件确定其系数，齿廓在旋转投影面上长度参数l＝(x12+y12)1/2-rp1，rp1为分度圆半径；
[0018]
c、将理论标准齿面和修形曲面进行叠加，获得齿廓修形齿面的位失rm，其表达式为
[0019]rm
(u1,θ1)＝r1(u1,θ1)+n1(u1,θ1)δ(l)
[0020]
齿廓修形齿面的单位法矢为
[0021][0022]
式中，修形齿面的两个切矢分别为
[0023][0024]
2、步骤(2)具体为：
[0025]
a、通过工件的位矢、法矢以及砂轮安装参数，推导出砂轮与工件的啮合方程为
[0026]
f(u1,θ1)＝(e
c-xm+p
1 cotσ)nz+
[0027]ec cotσny+zmn
x
＝0
[0028]
式中，xm、ym、zm和nx、ny、nz分别为经过齿廓修形后齿轮位矢rm和单位法矢nm的三
个分量；σ为砂轮安装角，ec是砂轮轴和工件轴之间的最短距离，ec＝rp1+rg，rp1为工件分度圆半径，rg为砂轮半径；
[0029]
b、推导砂轮与齿轮接触线方程，联立求解式rm(u1,θ1)＝r1(u1,θ1)+n1(u1,θ1)δ(l)、)δ(l)、求出转角时工件上的接触线l1；将工件上的接触线l1通过坐标转换到砂轮参考坐标系下sc，获得砂轮接触线lc的位矢和法矢
[0030]
rc(u1,θ1)＝m
cfmf1
r1(u1,θ1)
[0031]
式中，矩阵mf1为酉矩阵
[0032][0033]
c、推导成形砂轮截面方程，将接触线绕砂轮轴线旋转投影到砂轮截面，即可得到成形砂轮截面方程
[0034][0035]
将砂轮上的接触线lc绕着工件轴线做螺旋运动，采用对称抛物线运动规律，表达式为
[0036][0037]
式中，αp为齿向抛物线修形系数；z1为工件的轴向坐标，在齿端处的最大修形量为δz，对应的砂轮中心变动量为
[0038][0039]
式中，βb为基圆螺旋角，αn为法向压力角，确定齿向抛物线运动系数αp，经过齿廓、齿向双向修形磨削后，小轮齿面方程表示为
[0040][0041]
式中，矩阵
[0042][0043]
3、步骤(3)具体为：
[0044]
a、磨削人字齿轮的限制条件：以右旋齿轮为例，齿槽右侧的磨削终止点满足如下方程
[0045][0046]
式中，第一个和第二个等式表示此时磨削右侧齿面的终止点，第三个等式为此时接触线方程；ra1为齿顶圆半径，b0为退刀槽尺寸，x
′
1，y
′
1，z
′
1分别为双向修形磨削齿面位矢的三个分量，砂轮外径上所对应的接触线方程为
[0047][0048]
式中，rf1为齿根圆半径，当砂轮磨削终止点时，通过砂轮接触线最低点绕着砂轮轴线旋转所形成的轨迹线和另一侧齿轮的退刀槽端面齿顶圆相交，确定最大砂轮半径，其几何条件为
[0049][0050]
式中，第一个等式表示考虑齿向修形后将砂轮接触线lc绕工件轴线进行螺旋运动，得到砂轮外径的轨迹；第二个等式是砂轮外径接触到轮齿另一侧齿槽端面的轴向位置关系；第三个等式是砂轮与另一侧轮齿在齿顶发生干涉的条件；
[0051]
(2)确定砂轮的最大直径：采用拟牛顿方法求得磨削齿槽右侧齿面终止点时的砂轮最大半径rgr，同样，磨削齿槽左侧齿面终止点时，用rf1代替式中的ra1，其它方程不变，求得磨削齿槽右侧齿面终止点时的砂轮最大半径rgl，最后砂轮的最大直径为
[0052]dg
＝2max(r
gr
,r
gl
)。
[0053]
本发明的优势在于：本发明可精确计算修形人字齿轮成形磨最大砂轮直径，有效的解决了以往工程上确定砂轮直径的经验性和近似性，满足高精度修形齿轮加工砂轮直径选择的需求。
附图说明
[0054]
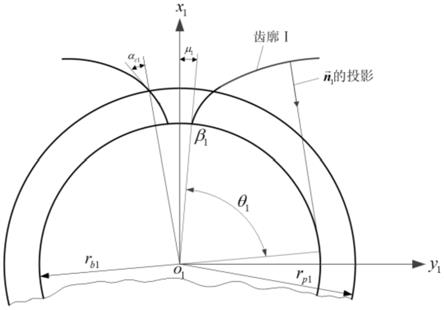
图1是渐开线端面齿廓；
[0055]
图2是旋转投影面上的齿廓修形曲线；
[0056]
图3是成形砂轮磨削原理；
[0057]
图4是齿向修形运动曲线。
具体实施方式
[0058]
下面结合附图举例对本发明做更详细地描述：
[0059]
本发明采用的技术方案为：一种修形人字齿轮成形磨最大砂轮直径精确设计方法，包括以下步骤：
[0060]
1、步骤一：建立齿轮齿廓为三段抛物线修形曲面模型。通过求解渐开线函数得到左、右旋齿轮齿面的位置矢量和法向矢量，进而得到人字齿轮齿面的数学模型。
[0061]
1.1、根据微分几何齿面共轭理论，确定的齿轮齿面的位置矢量和法向矢量分别为
[0062][0063][0064]
式中，r
b1
为基本半径；μ1为基圆上齿槽宽对所应的半角；θ1为渐开线上点的展开角；螺旋参数p1＝r
b1
tgλ
b1
，λ
b1
为齿轮基圆上的导程角；上标表示右侧齿面，下标表示左侧齿面。依此类推，可求得左旋齿轮左、右齿面的位矢和法矢。改变轮齿的旋向，即可获得人字齿轮另一侧齿面的数学模型。
[0065]
1.2、在齿轮旋转投影面上，根据几何关系，建立齿廓三段抛物线修形的函数表达式：
[0066][0067]
式中，l1表示齿根修缘长度，l2表示中间鼓形长度，l3表示齿顶修缘长度，a1、a2和a3为第i段抛物线系数；b1为第ii段抛物线系数；c1、c2和c3为第iii段抛物线系数。根据每段抛物线的最大修形量，以及相邻抛物线在连接点的连续相切条件确定其系数，齿廓在旋转投影面上长度参数l＝(x
12
+y
12
)
1/2-r
p1
，r
p1
为分度圆半径。
[0068]
1.3、将理论标准齿面和修形曲面进行叠加，获得齿廓修形齿面的位失rm，其表达式为
[0069]rm
(u1,θ1)＝r1(u1,θ1)+n1(u1,θ1)δ(l)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0070]
齿廓修形齿面的单位法矢为
[0071][0072]
式中，修形齿面的两个切矢分别为
[0073][0074]
2、步骤二：通过工件的位矢、法矢以及砂轮安装参数，推导出砂轮与工件的啮合方程，进而得到砂轮与工件接触线方程；并将接触线绕砂轮轴线旋转投影到砂轮截面，得到成形砂轮截面。同时考虑砂轮中心距变动，实现人字齿轮的双向修形。
[0075]
2.1、通过工件的位矢、法矢以及砂轮安装参数，推导出砂轮与工件的啮合方程为
[0076]
f(u1,θ1)＝(e
c-xm+p1cotσ)nz+
[0077]
eccotσny+zmn
x
＝0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(6)
[0078]
式中，xm，ym，zm和n
x
，ny，nz分别为经过齿廓修形后齿轮位矢rm和单位法矢nm的三个分量；σ为砂轮安装角，ec是砂轮轴和工件轴之间的最短距离，ec＝r
p1
+rg，r
p1
为工件分度圆半径，rg为砂轮半径。
[0079]
2.2、推导砂轮与齿轮接触线方程。联立求解式(4)-(6)，即可求出某一转角时(假设)工件上的接触线l1；将工件上的接触线l1通过坐标转换到砂轮参考坐标系下sc，获得砂轮接触线lc的位矢和法矢
[0080]
rc(u1,θ1)＝m
cfmf1
r1(u1,θ1)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(7)
[0081]
式中，矩阵m
f1
为酉矩阵
[0082][0083]
2.3、推导成形砂轮截面方程。将接触线绕砂轮轴线旋转投影到砂轮截面，即可得到成形砂轮截面方程
[0084][0085]
将砂轮上的接触线lc绕着工件轴线做螺旋运动。若考虑齿向修形，则通过改变砂轮轴线与工件轴线的中心距来实现的，磨削时砂轮中心的运动轨迹，采用对称抛物线运动
规律，表达式为
[0086][0087]
式中，α
p
为齿向抛物线修形系数；z1为工件的轴向坐标。在齿端处的最大修形量为δz，对应的砂轮中心变动量为
[0088][0089]
式中，βb为基圆螺旋角，αn为法向压力角。由此，可确定齿向抛物线运动系数α
p
。经过齿廓、齿向双向修形磨削后，小轮齿面方程表示为
[0090][0091]
式中，矩阵
[0092][0093]
3、步骤三：根据砂轮磨削齿面终止点时的几何条件，计算砂轮最大直径。
[0094]
3.1、磨削人字齿轮的限制条件。以右旋齿轮为例，齿槽右侧的磨削终止点应满足如下方程
[0095][0096]
式中，第一个和第二个等式表示此时磨削右侧齿面的终止点，第三个等式为此时接触线方程；r
a1
为齿顶圆半径，b0为退刀槽尺寸，x
′1，y
′1，z
′1分别为双向修形磨削齿面位矢的三个分量。此时，砂轮外径上所对应的接触线方程为
[0097][0098]
式中，r
f1
为齿根圆半径。当砂轮磨削终止点时，通过砂轮接触线最低点绕着砂轮轴线旋转所形成的轨迹线和另一侧齿轮的退刀槽端面齿顶圆相交，确定最大砂轮半径，其几何条件为
[0099][0100]
式中，第一个等式表示考虑齿向修形后将砂轮接触线lc绕工件轴线进行螺旋运
动，得到砂轮外径的轨迹；第二个等式是砂轮外径接触到轮齿另一侧齿槽端面的轴向位置关系；第三个等式是砂轮与另一侧轮齿在齿顶发生干涉的条件。
[0101]
3.2、确定砂轮的最大直径。上述方程组(12)～(14)包括有7个未知数，共有7个约束方程，因此方程组有解，采用拟牛顿方法可求得磨削齿槽右侧齿面终止点时的砂轮最大半径r
gr
。同样，磨削齿槽左侧齿面终止点时，用r
f1
代替式(12)中的r
a1
，其它方程不变，求得磨削齿槽右侧齿面终止点时的砂轮最大半径r
gl
，最后砂轮的最大直径为
[0102]dg
＝2max(r
gr
,r
gl
)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(15)
[0103]
结合图1-4，进行具体说明：
[0104]
本实施例一种修形人字齿轮成形磨最大砂轮直径精确设计方法，包括以下步骤：
[0105]
步骤一：图1为在x1y1z1三维直角平面内，用平面z1＝0截得人字齿轮一侧的齿面在端截面内的齿廓，轴线x1是齿槽的对称轴，β1为齿廓曲线ⅰ与基圆的交点，基圆上齿槽宽对所应的半角μ1是由轴x1和位置矢量o1β1构成的，并且μ1＝π/2z-invα
t
，其中z为齿轮齿数，α
t
为分度圆的压力角，渐开线函数invα
t
＝tanα
t-α
t
，则齿轮齿面的位置矢量和法向矢量分别为：
[0106][0107][0108]
式中，r
b1
为基本半径；μ1为基圆上齿槽宽对所应的半角；θ1为渐开线上点的展开角；螺旋参数p1＝r
b1
tgλ
b1
，λ
b1
为齿轮基圆上的导程角；上标表示右侧齿面，下标表示左侧齿面。依此类推，可求得左旋齿轮左、右齿面的位矢和法矢。改变轮齿的旋向，即可获得人字齿轮另一侧齿面的数学模型。
[0109]
图2为在齿轮旋转投影面上，建立齿廓三段抛物线修形的函数表达式，横坐标为渐开线旋转半径到分度圆的长度，纵坐标为修形量。将整个齿廓划分为三段，分别为l1，l2和l3，其中l1表示齿根修缘长度，l2表示中间鼓形长度，l3表示齿顶修缘长度，三段修形曲线对应的最大修形量分别为h1，h2和h3。根据几何关系，建立齿廓三段抛物线修形的函数表达式为
[0110][0111]
式中，l1表示齿根修缘长度，l2表示中间鼓形长度，l3表示齿顶修缘长度，a1、a2和a3为第i段抛物线系数；b1为第ii段抛物线系数；c1、c2和c3为第iii段抛物线系数。根据每段抛物线的最大修形量，以及相邻抛物线在连接点的连续相切条件确定其系数，齿廓在旋转投影面上长度参数l＝(x
12
+y
12
)
1/2-r
p1
，r
p1
为分度圆半径。
[0112]
将理论标准齿面和修形曲面进行叠加，获得齿廓修形齿面的位失rm，其表达式为
[0113]rm
(u1,θ1)＝r1(u1,θ1)+n1(u1,θ1)δ(l)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0114]
齿廓修形齿面的单位法矢为
[0115][0116]
式中，修形齿面的两个切矢分别为
[0117][0118]
步骤二：求解成形砂轮截形。图3为成形砂轮磨削斜齿轮的坐标系，其中坐标系sc、sf和s1分别为砂轮参考坐标系、工件参考坐标系和工件动坐标系。r
p1
为工件分度圆半径，rg为砂轮半径，ec是砂轮轴和工件轴之间的最短距离，砂轮安装角σ＝π/2-β，β为工件在分度圆上的螺旋角。
[0119]
成形砂轮磨削人字齿轮原理与磨削斜齿轮基本相同，不同之处在于需考虑退刀槽尺寸对砂轮最大直径选择的影响。采用成形砂轮磨削工件时的的啮合条件是，具有齿廓修形的齿面σ1与砂轮面σg之间的接触线的法矢通过砂轮回转轴线。通过工件的位矢、法矢以及砂轮安装参数，推导出砂轮与工件的啮合方程为
[0120]
f(u1,θ1)＝(e
c-xm+p1cotσ)nz+
[0121]
eccotσny+zmn
x
＝0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(6)
[0122]
式中，xm，ym，zm和n
x
，ny，nz分别为经过齿廓修形后齿轮位矢rm和单位法矢nm的三个分量，中心距ec＝r
p1
+rg。
[0123]
联立求解式(4)-(6)，即可求出某一转角时(假设)工件上的接触线l1；将工件上的接触线l1通过坐标转换到砂轮参考坐标系下sc，获得砂轮接触线lc的位矢和法矢
[0124]
rc(u1,θ1)＝m
cfmf1
r1(u1,θ1)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(7)
[0125]
式中，矩阵m
f1
为酉矩阵，
[0126][0127]
将接触线绕砂轮轴线旋转投影到砂轮截面，即可得到成形砂轮截面，
[0128][0129]
该砂轮截面可用于金刚石滚轮圆弧修整成形砂轮轮廓的修形轨迹计算。将砂轮上的接触线lc绕着工件轴线做螺旋运动，即可得到采用成形砂轮磨削具有齿廓修形的工件齿面。若考虑齿向修形，则通过改变砂轮轴线与工件轴线的中心距来实现的，图4为磨削时砂轮中心的运动轨迹，采用对称抛物线运动规律，表达式为
[0130][0131]
式中，α
p
为齿向抛物线修形系数；z1为工件的轴向坐标。在齿端处的最大修形量为δz，对应的砂轮中心变动量为
[0132][0133]
式中，βb为基圆螺旋角，αn为法向压力角。由此，可确定齿向抛物线运动系数α
p
。经过齿廓、齿向双向修形磨削后，小轮齿面方程表示为
[0134][0135]
式中，矩阵
[0136][0137]
步骤三：确定最大砂轮直径。磨削人字齿轮时，砂轮靠近退刀槽齿端时，需要考虑退刀槽尺寸与砂轮直径之间的关系，在不发生干涉的前提下，才能完成整个齿面的磨削。磨削时，砂轮与工件的接触线与螺旋线方向大致相同，仅是接触线的倾斜角度及弯曲程度不同。对于右旋齿轮，齿槽右侧齿面齿顶点是右侧磨削终止点，而齿槽左侧齿面齿根点是左侧齿面的磨削终止点；对于左旋齿轮，齿槽右侧齿面齿根点是磨削终止点，齿槽左侧齿面齿顶点是磨削终止点。现以右旋齿轮为例，齿槽右侧的磨削终止点应满足如下方程
[0138][0139]
式(12)中，第一个和第二个等式表示此时磨削右侧齿面的终止点，第三个等式为此时接触线方程；r
a1
为齿顶圆半径，b0为退刀槽尺寸，x
′1，y
′1，z
′1分别为双向修形磨削齿面位矢的三个分量。此时，砂轮外径上所对应的接触线方程为
[0140][0141]
式中，r
f1
为齿根圆半径。当砂轮磨削终止点时，通过砂轮接触线最低点绕着砂轮轴线旋转所形成的轨迹线和另一侧齿轮的退刀槽端面齿顶圆相交，确定最大砂轮半径，其几何条件为
[0142][0143]
式中，第一个等式表示考虑齿向修形后将砂轮接触线lc绕工件轴线进行螺旋运动，得到砂轮外径的轨迹；第二个等式是砂轮外径接触到轮齿另一侧齿槽端面的轴向位置关系；第三个等式是砂轮与另一侧轮齿在齿顶发生干涉的条件。上述方程组(12)～(14)包括有7个未知数，共有7个约束方程，因此方程组有解，采用拟牛顿方法可求得磨削齿槽右侧齿面终止点时的砂轮最大半径r
gr
。同样，磨削齿槽左侧齿面终止点时，用r
f1
代替式(12)中的r
a1
，其它方程不变，求得磨削齿槽右侧齿面终止点时的砂轮最大半径r
gl
，最后砂轮的最大直径为
[0144]dg
＝2max(r
gr
,r
gl
)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(15)。