一种空间变异非平稳地震动时程的模拟方法

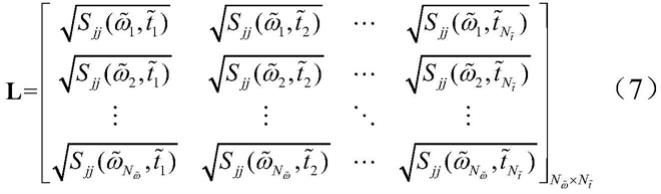
1.本发明涉及土木工程抗震设计技术领域，更具体地说，它涉及一种空间变异非平稳地震动时程的模拟方法。


背景技术：

2.根据抗震规范的要求，在大跨度结构抗震设计时，需要进行空间变异地震动作用下的非线性动力时程分析。而实测地震记录往往不足，因此需要通过数值模拟的方式获得大量的反映真实地震动特性的地震动时程。
3.当前针对空间变异非平稳地震动时程的模拟主要是基于表征地震动特性的非平稳功率谱模型、相干函数模型，采用谱表示法进行模拟。为了提高空间多点地震动场的模拟效率，一般采用本征正交分解(pod)等手段对完全非平稳的功率谱函数进行解耦，然后引入快速傅里叶变换(fft)。然而对于模拟点数较大，时间离散点和频率离散点较多的情况，解耦计算需要的计算机内存和耗时相当大。这导致空间变异非平稳地震动场的模拟效率低下。
4.因此需要提出一种更为高效的空间变异非平稳地震动场的谱表示模拟方法，以解决上述问题。


技术实现要素：

5.本发明的目的是针对上述技术问题，提供一种空间变异非平稳地震动时程的模拟方法。
6.本发明的上述技术目的是通过以下技术方案得以实现的：一种空间变异非平稳地震动时程的模拟方法，具体包括以下步骤：
7.s1、基于给定的地震动相干函数γ(ω)和功率谱密度函数s(ω,t)确定频率插值点和时频插值点
8.s2、计算频率插值点处待模拟的n点地震动场的延迟相干矩阵计算时频插值点处n个地震动模拟点的自演化功率谱
9.s3、对执行cholesky分解得到通过本征正交分解(pod)将分解为少量的主坐标和特征向量
10.s4、由和插值得到b(ω)、和
11.s5、基于谱表示法的随机模拟公式，利用快速傅里叶变换(fft)生成空间多点地震动样本。
12.进一步地，步骤s1的具体方法为：
13.(1)确定频率插值点选取均匀分布的频率插值点：
[0014][0015]
其中，ω1和ωu分别是第一个频率点和最后一个频率点，为频率插值点个数，满足n为频率离散点的总数；
[0016]
(2)确定时频插值点选取均匀分布的时频插值点确定方式如下：
[0017][0018][0019]
式中，t0是功率谱的总时长；和分别为沿频率和时间方向的时频插值点个数；且m为时间离散点的总数。
[0020]
进一步地，步骤s2的具体方法为：
[0021]
通过代入频率插值点的取值到相干函数，计算延迟相干矩阵为：
[0022][0023]
然后，采用上述相同的方式代入时频插值点的时间和频率取值，求得每一个地震动模拟点的自演化功率谱
[0024]
进一步地，步骤s3的具体方法为：
[0025]
(1)对执行cholesky分解得到并将分解为：
[0026][0027]
式中，上标t表示矩阵或向量的转置，是下三角矩阵，表示为：
[0028][0029]
(2)通过pod分解每一个得到相应的主坐标和特征向量
[0030]
(3)将所有时频插值点处的取值表示为一个常数矩阵，即：
[0031][0032]
将该常数矩阵的每一列均看作为一个列向量，共个列向量，通过以下特征向量分解：
[0033][0034]
找到一组最优的标准正交基所述列向量的投影将在其上最大化，式中φq为第q个特征向量；λq为第q个特征值；r为这个列向量的相关矩阵，可由下式计算：
[0035][0036]
在求得个特征向量后，每一个列向量的投影即主坐标，由下式确定：
[0037][0038]
其中，aq为第q个投影向量；
[0039]
(4)对特征值进行降序重组，保留含有较多能量的低阶特征值，l近似地表示为：
[0040][0041]
其中，n
φ
为满足精度要求所选择的低阶项的个数。基于上式，每一个用它的主坐标和特征向量表示为：
[0042][0043]
其中，和分别为向量aq和φq对应的离散函数。
[0044]
进一步地，步骤s4的具体方法为：
[0045]
在求得插值点处的和后，其他时频坐标处的b(ω)、和采用插值技术近似计算，并根据插值结果，近似重构出在原始时间和频率坐标处的结果，即：
[0046][0047]
进一步地，步骤s5的具体方法为：
[0048]
(1)基于谱表示方法，任意随机过程的模拟公式为：
[0049][0050]
式中，t是时间坐标；ω
l
是第l个频率点；δω是频率间隔；e是指数函数；i是虚数单位；φ
kl
是一组随机相位角，对于具体的样本为确定量；re表示获取复数的实部；h
jk
(ω,t)为分解后谱矩阵的元素，由下式计算：
[0051][0052]
其中，θ
jk
(ω)是h
jk
(ω,t)的相位角，对于地震动，其等于相干函数γ
jk
(ω)的相位角；
[0053]
(2)将式(13)(15)代入式(14)，得到如下模拟公式：
[0054][0055]
并通过交换求和顺序可得：
[0056][0057]
则将式(17)进行nn
φ
次fft操作，即生成空间n点地震动样本。
[0058]
综上所述，本发明具有以下有益效果：
[0059]
1、本发明的方法模拟完全非平稳地震动，仅需要在少量频率插值点处做cholesky分解，其余频点的结果通过插值近似获得，大大简化了谱矩阵分解的计算。此外，仅仅对少量时间-频率插值点处的功率谱函数进行pod解耦，其余时频点的解耦结果通过插值近似获得，大大减少了时频函数解耦的计算量。最后，进一步减少了fft操作次数。在保持足够精度的条件下，整个地震动模拟过程的效率被大大提高。
[0060]
2、本发明的方法可为大跨度结构，如输电塔线体系、输油管道等抗震设计的时程分析提供输入的地震动荷载时程。
附图说明
[0061]
图1是本发明实施例中的流程图；
[0062]
图2是本发明实施例中模拟地震动的相关函数验证曲线图；
具体实施方式
[0063]
以下结合附图1对本发明作进一步详细说明。
[0064]
实施例：一种空间变异非平稳地震动时程的模拟方法，如图1所示，具体包括以下步骤：
[0065]
s1、基于给定的地震动相干函数γ(ω)和功率谱密度函数s(ω,t)确定频率插值点和时频插值点具体方法为：
[0066]
(1)确定频率插值点选取均匀分布的频率插值点：
[0067][0068]
其中，ω1和ωu分别是第一个频率点和最后一个频率点，为频率插值点个数，满足n为频率离散点的总数；
[0069]
(2)确定时频插值点选取均匀分布的时频插值点确定方式如下：
[0070][0071][0072]
式中，t0是功率谱的总时长；和分别为沿频率和时间方向的时频插值点个数；且m为时间离散点的总数。
[0073]
s2、计算频率插值点处待模拟的n点地震动场的延迟相干矩阵计算时频插值点处n个地震动模拟点的自演化功率谱具体方法为：
[0074]
通过代入频率插值点的取值到相干函数，计算延迟相干矩阵为：
[0075][0076]
然后，采用上述相同的方式代入时频插值点的时间和频率取值，求得每一个地震动模拟点的自演化功率谱
[0077]
s3、对执行cholesky分解得到通过本征正交分解(pod)将分解为少量的主坐标和特征向量具体方法为：
[0078]
(1)对执行cholesky分解得到并将分解为：
[0079][0080]
式中，上标t表示矩阵或向量的转置，是下三角矩阵，表示为：
[0081][0082]
(2)通过pod分解每一个得到相应的主坐标和特征向量
[0083]
(3)将所有时频插值点处的取值表示为一个常数矩阵，即：
[0084][0085]
将该常数矩阵的每一列均看作为一个列向量，共个列向量，通过以下特征向量分解：
[0086][0087]
找到一组最优的标准正交基所述列向量的投影将在其上最大化，式中φq为第q个特征向量；λq为第q个特征值；r为这个列向量的相关矩阵，可由下式计算：
[0088][0089]
在求得个特征向量后，每一个列向量的投影即主坐标，由下式确定：
[0090][0091]
其中，aq为第q个投影向量；
[0092]
(4)对特征值进行降序重组，保留含有较多能量的低阶特征值，l近似地表示为：
[0093][0094]
其中，n
φ
为满足精度要求所选择的低阶项的个数。由此每一个用它的主坐标和特征向量表示为：
[0095][0096]
其中，和分别为向量aq和φq对应的离散函数。
[0097]
s4、由和插值得到b(ω)、和具体方法为：
[0098]
在求得插值点处的和后，其他时频坐标处的b(ω)、和采用插值技术近似计算，并根据插值结果，近似重构出在原始时间和频率坐标处的结果，即：
[0099][0100]
s5、基于谱表示法的随机模拟公式，利用快速傅里叶变换(fft)生成空间多点地震动样本，具体方法为：
[0101]
(1)基于谱表示方法，任意随机过程的模拟公式为：
[0102][0103]
式中，t是时间坐标；ω
l
是第l个频率点；δω是频率间隔；e是指数函数；i是虚数单位；φ
kl
是一组随机相位角，对于具体的样本为确定量；re表示获取复数的实部；h
jk
(ω,t)为分解后谱矩阵的元素，由下式计算：
[0104][0105]
其中，θ
jk
(ω)是h
jk
(ω,t)的相位角，对于地震动，其等于相干函数γ
jk
(ω)的相位角；
[0106]
(2)将式(13)(15)代入式(14)，得到如下模拟公式：
[0107][0108]
并通过交换求和顺序可得：
[0109][0110]
则将式(17)进行nn
φ
次fft操作，即生成空间n点地震动样本。
[0111]
以下模拟一个水平分布的非平稳地震动场为例对本发明的方法进行进一步说明：
[0112]
(1)模拟点为沿着2000m水平直线方向均匀分布的50个点。
[0113]
(2)假定各点的自演化功率谱密度函数为：
[0114][0115]
其中，零均值平稳过程具有相同的功率谱密度，描述为kanai-tajimi谱：
[0116][0117]
其中，s0＝0.1cm2/s3；对于k1(f)，取f
g1
＝15/(2π)hz；对于k2(f)，取f
g2
＝5/(2π)hz；ζg＝0.25。一般时间调制函数为：
[0118][0119]
其中，c＝0.125和d＝0.25。
[0120][0121]
其中，ε＝16s和μ＝4s。
[0122]
考虑时不变相干函数为：
[0123]
[0124][0125]
θ(f)＝θ0[1+(f/f0)b]-1/2
[0126]
其中，v
jk
表示两点之间的距离；v是波的传播速度，取v＝2000m/s；α＝0.147；β＝0.736；θ0＝5210m/s；f0＝1.09hz；和b＝2.67。
[0127]
(3)基于上述定义的地震演化功率谱密度函数和相干函数，确定均匀分布的频率插值点
[0128][0129]
其中，ω1和ωu分别是第一个频率点和最后一个频率点，分别取为0.0767rad/s和50πrad/s，为相干函数频率插值点个数，取48，满足n为频率离散点的总数，n取2048；
[0130]
确定时间-频率插值点各点坐标为：
[0131][0132][0133]
其中，ω1取0.0767rad/s，ωu取50πrad/s，t0取40.96s，为演化功率谱密度函数频率插值点个数，取64，为演化功率谱密度函数时间插值点个数，取48。
[0134]
(4)计算频率插值点处待模拟的n点地震动场的延迟相干矩阵计算时频插值点处n个地震动模拟点的自演化功率谱具体方法为：
[0135]
通过代入频率插值点的取值到相干函数，计算延迟相干矩阵为：
[0136][0137]
然后，采用上述相同的方式代入时频插值点的时间和频率取值，求得每一个地震动模拟点的自演化功率谱
[0138]
(5)对执行cholesky分解得到通过本征正交分解(pod)将分解为少量的主坐标和特征向量具体方法为：
[0139]
对执行cholesky分解得到并将分解为：
[0140][0141]
式中，上标t表示矩阵或向量的转置，是下三角矩阵，表示为：
[0142][0143]
通过pod分解每一个得到相应的主坐标和特征向量
[0144]
将所有时频插值点处的取值表示为一个常数矩阵，即：
[0145][0146]
将该常数矩阵的每一列均看作为一个列向量，共个列向量，通过以下特征向量分解：
[0147][0148]
找到一组最优的标准正交基所述列向量的投影将在其上最大化，式中φq为第q个特征向量；λq为第q个特征值；r为这个列向量的相关矩阵，可由下式计算：
[0149][0150]
在求得个特征向量后，每一个列向量的投影即主坐标，由下式确定：
[0151][0152]
其中，aq为第q个投影向量；
[0153]
对特征值进行降序重组，保留含有较多能量的低阶特征值，l近似地表示为：
[0154][0155]
其中，n
φ
为满足精度要求所选择的低阶项的个数，取n
φ
＝4。由此每一个用它的主坐标和特征向量表示为：
[0156][0157]
其中，和分别为向量aq和φq对应的离散函数。
[0158]
(6)由和插值得到b(ω)、和具体方法为：
[0159]
在求得插值点处的和后，其他时频坐标处的b(ω)、和采用插值技术近似计算，并根据插值结果，近似重构出在原始时间和频率坐标处的结果，即：
[0160][0161]
(7)基于谱表示法的随机模拟公式，利用快速傅里叶变换(fft)生成空间多点地震动样本，具体方法为：
[0162]
基于谱表示方法，任意随机过程的模拟公式为：
[0163][0164]
式中，n为频率步数，取2048，δω＝ωu/n为频率增量，ω
l
＝lδω为频率点坐标，t是时间坐标；ω
l
是第l个频率点；e表示指数函数；i是虚数单位；φ
kl
是一组随机相位角，在[0,2π]范围内均匀分布，对于具体的样本为确定量；re表示获取复数的实部；h
jk
(ω,t)为分解后谱矩阵的元素，由下式计算：
[0165][0166]
其中，θ
jk
(ω)是h
jk
(ω,t)的相位角，对于地震动而言，其等于相干函数γ
jk
(ω)的相位角；
[0167]
由上述得到如下多点地震动的模拟公式：
[0168][0169]
并通过交换求和顺序可得：
[0170][0171]
则将上式进行nn
φ
次fft操作，即生成地震动样本。
[0172]
通过上述模拟方法，可模拟出地震场中50个点的地震动时程，并计算1000个样本的自相关函数和互相关函数，然后与给定的目标值进行比对。图2分别给出了模拟地震动时程的自相关函数和互相关函数的验证结果，由图可知，模拟值与目标值保持一致，从而可以说明模拟方法的合理性。进一步，将本发明方法的模拟效率与传统方法进行对比，结果显示本发明方法模拟一个样本仅需要4.2秒，而传统方法则需要149.9秒，可见采用本发明方法，模拟效率被大大提高。
[0173]
在本发明的上述实施例中，采用本发明的方法模拟完全非平稳地震动，仅需要在少量频率插值点处做cholesky分解，其余频点的结果通过插值近似获得，大大简化了谱矩阵分解的计算。此外，仅仅对少量时间-频率插值点处的功率谱函数进行pod解耦，其余时频点的解耦结果通过插值近似获得，大大减少了时频函数解耦的计算量。最后，进一步减少了fft操作次数。在保持足够精度的条件下，整个地震动模拟过程的效率被大大提高。本发明的方法可为大跨度结构，如输电塔线体系、输油管道等抗震设计的时程分析提供输入的地
震动荷载时程。
[0174]
本具体实施例仅仅是对本发明的解释，其并不是对本发明的限制，本领域技术人员在阅读完本说明书后可以根据需要对本实施例做出没有创造性贡献的修改，但只要在本发明的权利要求范围内都受到专利法的保护。