应用于计及电动汽车充放电选择的充放电电价的定价方法与流程

1.本发明涉及充放电电价的定价领域，具体而言，涉及应用于计及电动汽车充放电选择的充放电电价的定价方法。


背景技术：

2.面对能源危机与环境污染的愈发严重，电能推广将逐渐降低汽车领域对汽油、柴油等燃料的消耗，缓解尾气排放带来的污染，使电动汽车成为未来交通领域的共同发展方向。而电动汽车的能源主要来自电网，其大规模发展离不开电力系统的支撑。据中国汽车工程协会预测，到2030年我国电动汽车保有量将达到8000万辆，若平均配备60kwh的动力电池，其等效储能量将达到48
×
108kwh，而我国2016年日上网电量仅为160
×
108kwh，庞大的能源需求无论是从系统吸收电能，还是向系统释放电能，量级均是可观的。因此，合理的电动汽车用户充放电行为优化管理，可在电能短缺时为电网提供电能补给，达到电力供需平衡，对提高电网安稳运行具有重大意义。
3.随着电动汽车与电网互动技术(vehicle-to-grid,v2g)的发展，电动汽车通过a/d和d/a装置既可以实现与电网的电能交换，也可以参与运营商充放电代理服务，从而实现了用户与电网、运营商之间能量与信息的友好互动。电网和运营商通过双向充放电装置配合电价优化策略与通讯系统调控，使得用户在电网用电低谷时，选择充电消纳电网过剩的电量，起到填谷的作用，并享受谷时段低廉的电价；在电网用电高峰时，作为分散式储能设备向电网提供电能，起到削峰的作用，并获得高峰低谷电价差作为放电报酬。因此，电网与运营商可以通过v2g技术优化电动汽车用户充放电行为，让更多用户参与到电网调峰与调频、协调消纳新能源等服务中来，为多个主体创造效益。而电价作为一种合理的电动汽车用户充放电行为优化管理方法，可通过调整电价的方式可以合理引导电动汽车用户分时段接入电网，一方面可提高电网安稳运行，另一方面可为电动汽车用户创造效益。
4.根据现有研究表明，电动汽车充放电定价优化方法仍存在一定局限性，主要表现为以下方面：1)在电价优化方面，从充电和放电两个维度兼顾多主体利益的研究较少；2)在对用户响应电价关联建模时，多是采用消费统计学或电力需求价格弹性分析进行关联建模，忽略了电动汽车用户在响应电价时存在的响应饱和区及死区的问题，难以体现出不同消费用户在响应电价上的差异；3)在对峰谷充放电价优化时，大多是强调引导用户降低电网峰谷差而保证电网安全运行，忽略了用户满意度及运营商成本投入，导致用户响应电价意愿不高涨和运营商成本增加的问题；4)针对定价优化模型的求解算法易陷入局部最优解，求解精度和效率有待进一步提升。
5.为解决现有电动汽车充放电电定价优化方法存在的问题，本发明提出了一种计及电动汽车用户充放电选择的充放电电价的定价方法，计及了用户响应与充放电价的关联性，兼顾电网负荷波动、用户满意度和运营商成本最优目标，基于免疫鱼群算法对电动汽车充放电定价进行优化。


技术实现要素：

6.本发明针对电动汽车充放电定价优化方法中存在的问题，针对电动汽车用户响应充放电价时存在的不确定行为，考虑了电网负荷波动性、运营商新增成本投入及用户响应用户的满意度，构建了计及用户响应电价关联和多主体共赢的电动汽车充放电定价多目标优化模型，并提出改进的免疫鱼群算法对模型进行优化求解。该方法构建了不同响应程度用户充放电转移与电价变化的关联模型，多目标电价优化方法可降低系统负荷峰谷差、减少运营商成本投入，最大程度提高用户响应电价的能力，提出的免疫鱼群算法可为电动汽车充放电精确定价提供决策依据，有利于电网安全平稳运行。
7.本发明采用的技术方案：
8.本发明中的电动汽车用户充放电选择的确定方法是通过激励政策或者电价优化方案来调整用户用电结构，从而减少某段时间内的充放电负荷。根据用户的消费心理，将电动汽车用户对电价的响应方式分为正常响应状态(即线性区)、响应极限的饱和状态(即饱和区)、无响应的截止状态(即死区)三种，每一种响应方式都会对应不同的负荷转移率曲线，为求解不同响应用户的负荷转移率曲线就要确定其斜率、响应饱和值、死区阈值。采用最小二乘法，通过充放电负荷的估计值和实际负荷最小化误差的平方和动态寻找充放电转移率曲线的最佳拟合曲线参数。而当最小二乘法在计算用户规模较大时，将导致拟合目标函数扰动项的方差不全相等存在异方差，使得拟合的参数值不是有效估计量是有偏的。因此，提出采用局部加权的最小二乘法消除异扰动项之间的异方差，使距离较近的点产生的影响大于距离较远的点。在电价调整后反复拟合，得到其斜率、响应饱和值、死区阈值，动态表征出不同时段下用户的负荷转移率与电价变化的关系。进而根据用户响应电价的方式，对响应充电电价、响应充放电价、无响应电价用户的充放电转移情况进行分析。
9.本发明中的充放电电价的定价模型，计及多主体电网公司、运营商和电动汽车用户的利益目标，结合电动汽车行程约束、电池负荷状态约束及充放电时间约束等。其中电网公司的利益目标为在调整电价改变用户充放电习惯时希望系统峰负荷、峰谷差越小越好。电动汽车运营商的利益目标为在投入成本的把控，即固定成本为充电站充电桩的建设，可变成本为充放电过程中的电能损失和电池寿命损耗折算成本。在峰谷充放电价调整后，可减少电动汽车在峰时段集中充放电导致的系统负荷波动和电能损失的成本投入。对于用户角度在调整电价的同时要保证用户的满意度最大，建立用户用电满意度模型。电动汽车行程约束为电动汽车在充电站向电网所放电量应保证在下一段行程所需足够的电量，其放电量应介于电池容量的最大值和最小值。电池负荷状态约束为电动汽车用户在进行充放电过程中应使得所充放电量保持在动力电池的容量的最大负荷电量与最小负荷电量之间。充放电时间约束为在停驶过程中电动汽车的充放电时间段应不大于前一段行驶时长与后一段行驶时长之差，并且满足每段充放电时长非负。并且用户可以在某一时段选择对电动汽车进行充电或放电，但是用户的充电过程与放电过程不能同时进行。
10.本发明中的充放电定价多目标模型求解方法是基于收缩空间的免疫鱼群模型求解算法。通过人工鱼群算法对多目标峰谷充放电价模型进行求解，并引入免疫算法解决算法容易早熟收敛至局部劣解的问题。免疫算法通常采用信息熵来计算抗体浓度，但存在计算相对复杂，且含有冗余计算信息等问题。采用距离矢量的方法减小搜索空间，规避了信息的重复计算。相邻点存储着到当前点的最优距离解，避免在迭代求解时重新计算已经迭代
过的点，降低信息计算的复杂度。其次，人工鱼群算法在优化求解后期出现鱼群趋同，丧失群体求解的多样性，导致优化结果陷入局部解。引入免疫算法产生多种抗体保持进化群体的多样性，避免早熟收敛至局部劣解。依次通过觅食行为、群聚行为和追尾行为对多目标峰谷充放电价模型进行求解，将抗体浓度概率作为人工鱼选择游向当前食物的选择概率，使得算法在模拟人工鱼群觅食求解时减少了到目标位置距离的冗余计算，并保证了从不同点觅食到最优解的矢量路径具有唯一性，避免了人工鱼群在优化求解中整个群体趋同的现象。
11.与现有技术相比，本发明的有益效果是：1.该方法兼顾充电和放电特性，构建了不同响应程度用户充放电转移与电价变化的关联模型，为运营商在调整电价引导有序充放电提供实用工具。2.多目标电价优化方法在降低系统负荷峰谷差、减少运营商成本投入的同时，最大程度提高用户响应电价的能力，实现对用户分时段接入电网的响应调控。3.提出的免疫鱼群算法可有效求解多主体共赢定价优化问题，避免求解过程早熟收敛而陷入局部劣解，为电动汽车充放电精确定价提供决策依据，有利于电网安全平稳运行。
附图说明
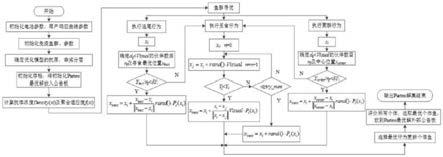
12.图1示出了本发明多目标优化模型求解流程图。
13.图2示出了本发明节省成本与峰谷差随用户满意度变化曲线。
14.图3示出了本发明用户满意度最大时不同响应用户的负荷曲线。
15.图4示出了本发明运营商投入最小时不同响应用户负荷曲线。
16.图5示出了本发明电价优化前后日负荷曲线。
17.图6示出了本发明多目标优化下不同响应用户负荷曲线。
具体实施方式
18.1、计及用户充放电选择的充放电行为分析
19.电动汽车响应电价的行为主要体现在负荷变化上，当电网系统稳定运行受到波动时，运营商通过激励策略或电价优化方案调整用户用电结构，从而减少某段时间内的充放电负荷。因此，用户对电价响应程度将是运营商制定电价的依据。
20.(1)局部加权最小二乘拟合用户充放电转移率曲线
21.根据用户的消费心理，将电动汽车用户对电价的响应方式分为正常响应状态(即线性区)、响应极限的饱和状态(即饱和区)、无响应的截止状态(即死区)三种，每一种响应方式都会对应不同的负荷转移率曲线，为求解不同响应用户的负荷转移率曲线就要确定其斜率、响应饱和值、死区阈值。将某日中时段a到时段b的充放电负荷转移率曲线表示为：
[0022][0023]
式中：k
ab
为响应度曲线的斜率；l
ab
为响应度曲线的截距，即响应的阈值；h
ab
为最大响应度阈值；为用户最大转移率；δx
ab
为时段a到时段b电费变化差值。
[0024]
因此，将电动汽车用户充放电的峰转平负荷曲线、峰转谷负荷曲线、平转谷负荷曲
线拟合负荷表示为：
[0025][0026]
式中：l
t0
、l
t
为电价变化前后t时段的负荷；lv、lf、l
p
为谷时段、平时段、峰时段总负荷的平均值；t
p
、tf、tv为峰、平、谷时段；为峰时段到平时段转移率；为峰时段到谷时段转移率；为平时段到谷时段转移率。
[0027]
为求解用户充放电转移率曲线的参数，采用最小二乘法，通过充放电负荷的估计值和实际负荷最小化误差的平方和动态寻找充放电转移率曲线的最佳拟合曲线参数，其拟合函数为：
[0028][0029]
式中：l
t,k
为电价调整第k次后用户拟合负荷；l'
t,k
为电价调整第k次后用户实际负荷。
[0030]
可得负荷转移率函数在δx
ab
电价调整第k次后，其估计转移率与实际转移率的最小二乘拟合转移率参数可表示为：
[0031][0032]
当最小二乘法在计算用户规模较大时，将导致拟合目标函数扰动项的方差不全相等存在异方差，使得拟合的参数值不是有效估计量是有偏的。因此，采用局部加权的最小二乘法消除异扰动项之间的异方差，使距离较近的点产生的影响大于距离较远的点，加权因子w(k)表示为：
[0033][0034]
得到局部加权最小二乘法拟合转移率参数表示为：
[0035][0036]
在电价调整后反复拟合，得到其斜率、响应饱和值、死区阈值，动态表征出不同时段下用户的负荷转移率与电价变化的关系。
[0037]
(2)不同用户响应电价程度关联分析
[0038]
由于用户消费心理的差异，充放电价的调整将改变当前时刻充放电模式选择。因此，根据用户响应电价的方式，对响应充电电价、响应充放电价、无响应电价用户的充放电转移情况进行分析。
[0039]
1)响应充电电价用户分析
[0040]
假设电动汽车用户某日的行程为m段，其中每一段行程i包含了s(i)个时间段。用户的每一段行程时段都存在着停驶和行驶的过程，而用户会根据实际情况选择在停驶过程中s(i)的第j个时段对电动汽车进行充放电。
[0041]
在充放电价调整后，响应充电电价的用户根据电价变化情况改变起始充电时刻及
充电时长，并享受优惠的电价支出。因此，电动汽车用户在第i段行程第j时刻开始充电转移至下一个优惠充电价格时刻k∈(j,j+1,...,j+12-t
i,jdown
)需要缴纳的电费为q
i.k
：
[0042][0043]
式中：t
i,jdown
为第i段行程j时段的充电时长；p
i,kdown
为第i段行程k时段的充电功率；ρ
i,kdown
为第i段行程k时段的充电电价；ωd为电池损耗费用率；η、η
down
为电网转换效率和充电效率，λ
down
为电池充电电量系数(量纲均为1)。
[0044]
因此，对于响应充电电价的用户，在电价调整后，第i段行程第j时刻移至k时刻的用户数量n
i,k1
为：
[0045][0046]
式中：n
i,k
为第i段行程k时刻行驶的电动汽车数量。
[0047]
2)响应充放电价用户分析
[0048]
在充放电价调整后，参与v2g放电的用户也会响应充电电价使得收益最大化，因此，此类用户的放电量在放电的过程中要保证下一段行程有足够的电量，而前一个充电时段所花费用要小于下一放电时刻收益。则电动汽车用户在j时刻放电所获得的利润q
i,jv2g
为：
[0049][0050]
式中：ρ
i,jup
为第i段行程k时段的放电电价；η
up
为放电效率，λ
up
为电池放电电量系数(量纲均为1)；p
i,jup
为第i段行程j时段的放电功率。
[0051]
j-1时刻电动汽车开始充电至与j时刻电动汽车放电相同时长所要交纳的电费q
i,j-1
为：
[0052][0053]
因此，对于响应充放电价的用户方式，在峰谷分时电价实施后，参与放电的第i段行程第j时刻的电动汽车数量为：
[0054][0055]
且满足放电所获得的利润与充电缴纳的电费为：
[0056][0057]
3)无响应电价用户分析
[0058]
在调整峰谷分时电价后，无响应的电动汽车用户既不改变充电时刻也不参与v2g放电，与电价调整前的充放电行为并无区别。因此，无响应电价用户充放电负荷变化与电价调整无关，则在第i段行程第j时刻的电动汽车数量n
i,j3
为：
[0059]
[0060]
得到在任意时刻下不同响应的平均总负荷为：
[0061][0062]
2、兼顾多主体利益共赢的充放电定价多目标优化模型
[0063]
在充放电定价变化后，电动汽车用户会根据实际情况调整自己的充放电方式与时间选择，平衡电费支出。但是，运营商在调整电价只保证电网与运营商利益最大化，将会影响用户参与响应电价的满意度，就会拒绝接纳优化方案，影响优化方案的正常实施，反过来只考虑用户用电满意度最大，将提高运营商投入成本，并增加电网系统负荷。因此，本专利建立了考虑电网峰谷差最小、运营商新增成本最小及用户用电满意度最大的多目标充放电价优化模型。
[0064]
(1)优化目标
[0065]
1)电网峰谷差最小化
[0066]
电网公司的利益目标为在调整电价改变用户充放电习惯时希望系统峰负荷、峰谷差越小越好。因此，电网公司的目标函数为：
[0067][0068][0069]
式中：ming1为峰负荷最小；ming2为峰谷差最小；l
t0
为原日负荷数据。
[0070]
2)运营商成本盈利最大化
[0071]
电动汽车运营商的利益目标为在投入成本的把控，即固定成本为充电站充电桩的建设，可变成本为充放电过程中的电能损失和电池寿命损耗折算成本。因此，假设运营商的固定成本投入一定下，尽量减少可变成本的投入，从而减少整体支出。所以，对于电动汽车在电网充放电过程中损耗的单位电能成本ce为：
[0072]ce
＝c
el
+ωdꢀꢀ
(17)
[0073]cel
为在充放电过程中由于能量转换所导致的单位电能损失成本，可表示为：
[0074][0075]
在峰谷充放电价调整后，可减少电动汽车在峰时段集中充放电导致的系统负荷波动和电能损失的成本投入为：
[0076][0077]
3)电动汽车用户用电满意度最大化
[0078]
充电站运营商与电网公司为避免新增运行成本的投入采取对峰谷充放电价调整，但电价将引起用户用电方式发生较大幅度的改变，会影响用户舒适度，导致其满意度下降，从而影响用户响应电价的能力。因此，对于用户角度在调整电价的同时要保证用户的满意度最大，建立用户用电满意度模型，表示为：
[0079][0080]
(2)约束条件
[0081]
约束条件包含电动汽车行程约束、电池负荷状态约束及充放电时间约束等。
[0082]
1)电动汽车行程约束
[0083]
电动汽车在充电站向电网所放电量应保证在下一段行程所需足够的电量，其放电量应介于电池容量的最大值和最小值，应满足：
[0084][0085]
其中，电池负荷状态soc与电池容量之间的乘积为动力电池剩余电量。式中：cb为电动汽车电池容量；d
i+1
为第i+1段行程的行驶距离；w为电动汽车动力电池平均每千米的耗电量；s
max
，s
min
，ss分别为电池荷电状态的最大值、最小值和初始值，量纲均为1。
[0086]
2)电池负荷状态约束
[0087]
电动汽车用户在进行充放电过程中应使得所充放电量保持在动力电池的容量的最大负荷电量与最小负荷电量之间，即所充电量应小于动力电池的最大负荷电量：
[0088][0089]
并且，电动汽车用户所放电量应为与当前电量的差值大于最低电量：
[0090][0091]
3)充放电时间约束
[0092]
在停驶过程中电动汽车的充放电时间段应不大于前一段行驶时长与后一段行驶时长之差，并且满足每段充放电时长非负，如式(24)、(25)所示。并且用户可以在某一时段选择对电动汽车进行充电或放电，但是用户的充电过程与放电过程不能同时进行，应满足：
[0093][0094][0095][0096]
式中：t
i,jdown
为电动汽车每日行程中第i段行程j时段的充电时长；t
i,jup
为第i段行程j时段里向电网放电时长；t
i,j
为第i段行程j时段；t
i,j+1
为第i段行程j+1时段。
[0097]
4)v2g放电电价约束
[0098]
根据运营商成本和放电补偿，设电动汽车参与放电固定成本折算成单位电量成本为cf，即单位电能补偿及单位放电电能消纳成本的价格为1.2美分/(kw
·
h)。因此，在制定电动汽车参与v2g放电获得的电价应满足：
[0099][0100]
(3)多目标模型
[0101]
综上所述，在满足电动汽车充放电习惯及电池特性约束下，综合考虑电网峰谷差、运营商成本投入最小化和用户用电满意度最大化，建立协调用户、电网与运营商之间利益的峰谷充放电价多目标模型：
[0102][0103]
式中：f＝(ming1，ming2，-maxcost，maxθ)为目标函数；x为由优化变量组成的向量组；u
k(x)
为模型的不等式约束函数。
[0104]
3、基于收缩空间的免疫鱼群模型求解算法
[0105]
在保证电网峰谷差、峰负荷最小化的目标下，要使用户用电满意度最大化和运营商投入最小化。显然，三者目标函数之间存在着互斥矛盾，而多目标优化的提出就是均衡各组解值找到满足条件的最优解。因此，在解决多目标问题时在人工鱼群算法的基础上结合免疫算法和pareto最优解集，设计基于收缩空间的多目标免疫鱼群算法(contraction space of multi-objective immune fish swarm algorithm,csmoifsa)。凭借人工鱼群算法动态求解收敛速度快的优势对多目标峰谷充放电价模型进行求解，并引入免疫算法解决算法容易早熟收敛至局部劣解的问题。
[0106]
(1)改进免疫鱼群算法
[0107]
1)基于收缩空间的免疫抗体浓度计算
[0108]
免疫算法通常采用信息熵来计算抗体浓度，但存在计算相对复杂，且含有冗余计算信息等问题。因此，采用距离矢量的方法减小搜索空间，规避了信息的重复计算。相邻点存储着到当前点的最优距离解，避免在迭代求解时重新计算已经迭代过的点，降低信息计算的复杂度。设优化解的适应度函数f(xi)和目标函数分别对应免疫算法的抗体和抗原，n个抗体组成一个非空集合x。将n个抗体进行聚类分层分为m层，所有抗体的适应度：
[0109][0110]
距离矢量d(xi,xk)是节点xi经过xk到达xj的距离，等于xi到相邻点xk的距离加上xk到xj的最短距离，表示为：
[0111][0112]
式中：δx为距离矢量的收敛步长；xk为节点xi相邻节点。
[0113]
设抗体f(xi)在集合x上的距离d(xi,x)为：
[0114]
[0115]
则抗体的浓度表示density(xi)为：
[0116][0117]
因此，从当前点xi到通过最优距离到达xj的抗体浓度概率选择ps(xi)为：
[0118][0119]
计算抗体与抗原的亲和度，表示抗体对抗原的识别程度，其亲和度mi为：
[0120][0121]
式中：opi(x)为所求问题的目标函数，即抗原。
[0122]
2)结合免疫抗体适应度的鱼群寻优方法
[0123]
由于人工鱼群算法在优化求解后期出现鱼群趋同，丧失群体求解的多样性，导致优化结果陷入局部解。因此，引入免疫算法产生多种抗体保持进化群体的多样性避免早熟收敛至局部劣解。将改进鱼群算法的抗体浓度概率选择作为人工鱼游向当前食物的选择概率，设第i条鱼的位置为xi，即为第i个抗体，其当前位置的食物浓度yi度设为该位置抗体的适应度值f(xi)，人工鱼从一个位置游到另外一个位置，即产生新的免疫抗体。并根据鱼群在寻食过程中的行为寻找最优解的位置。
[0124]
①
觅食行为
[0125][0126]
式中：visual为人工鱼随机视野范围；x
inext
为第i条人工鱼游动的下一位置；ps(xi)为人工鱼选择游向当前食物的选择概率；rand()为第i条人工鱼游动的随机变量，取值为0到1之间；xj为第i条人工鱼随机视野范围内另一位置，该位置的食物浓度为yj。
[0127]
②
聚群行为
[0128][0129]
式中：δ为拥挤因子；nf为视野范围内个体鱼数量；x
center
为鱼群游动时的中心位置，该位置的食物浓度为y
center
。
[0130]
③
追尾行为
[0131][0132]
式中：x
best
为第i条人工鱼寻食最优位置，该位置的食物浓度为y
best
。
[0133]
将抗体浓度概率作为人工鱼选择游向当前食物的选择概率，使得算法在模拟人工鱼群觅食求解时减少了到目标位置距离的冗余计算，并保证了从不同点觅食到最优解的矢
量路径具有唯一性，避免了人工鱼群在优化求解中整个群体趋同的现象。
[0134]
(2)充放电价模型求解步骤
[0135]
多目标免疫鱼群算法是在原有算法所求得的多个解中寻找出更优的pareto解集，使得在其它目标下非劣最优解函数构成非劣最优目标域，从而解决多个目标制约的优化问题，多目标模型求解步骤如下：
[0136]
step 1：参数初始化。输入电动汽车电池参数、用户响应度曲线参数值初始值；
[0137]
step 2：多目标免疫鱼群初始化。在求解空间内随机初始化s个抗体(即个体人工鱼)，设定个体鱼的维度为峰平谷充放电价，每个个体鱼对应不同时段充放电价，生成人工鱼群m，迭代次数k；
[0138]
step 3：目标函数确定。将充放电价多目标优化模型的目标函数fi(x)与不等式约束函数uk(x)作为抗原，并采用分层聚类法对种群进行分层，将每一层所有个体人工鱼赋值到初始pareto解公告板中；
[0139]
step 4：寻优过程。通过模拟人工鱼生物行为，选择在人工鱼聚群觅食过程中行为最优的人工鱼，更新个体鱼；
[0140]
①
觅食行为。在第i条人工鱼当前位置xi的随机视野范围内另一位置xj，判断是否满足yj》yi，满足则个体向该方向移动；否则，再次随机选择下一位置xj。反复判断下一位置是否满足移动条件，如果仍不满足前进条件，则随机向前移动。
[0141]
②
追尾行为。计算在第i条人工鱼当前位置xi的随机视野范围内(即||x
i-xj||《visual)伙伴数目nf，找到伙伴中寻食最优位置x
best
，当满足y
best
/nf》δyi时，说明处于x
best
位置伙伴的鱼群拥挤程度低且周围实物浓度高，就向x
best
位置方向移动一步；否则执行觅食行为。
[0142]
③
聚群行为。计算在第i条人工鱼当前位置xi的随机视野范围内伙伴数目nf和其中心位置x
center
，当满足y
center
/nf》δyi时，就向该位置方向移动一步；否则执行觅食行为。
[0143]
step 5：评价所有抗原与抗体(人工鱼)之间的亲和度，选取亲和度最高的个体鱼赋给公告板，更新parteo最优解外部公告板；
[0144]
step 6：判断是否满足最大迭代数，如果满足则输出最优峰谷充放电价解集，停止迭代；否则转至step 3。
[0145]
求解流程如图1所示。
[0146]
4、实验算例与分析
[0147]
(1)实验数据与参数设置
[0148]
由于电动汽车电池种类较多，本专利主要以车载动力电池占比较高的尼桑与比亚迪电动汽车的锂离子电池和磷酸锂铁电池为基础进行分析(记为ns电池和byd电池)，其主要的参数如表1所示。
[0149]
表1电动汽车电池参数
[0150][0151]
设定电动汽车在充放电过程中，其电池的最小负荷状态为15％和最大负荷状态为
95％；电动汽车在充放电时电池的转化效率η
up
和η
down
为0.97；电网在转换电动汽车充放电效率为0.85；v2g充放电量系数λ
down
和λ
up
均为0.1。并根据目前电动汽车比亚迪和尼桑占有量可知，两种类型车辆的比例为1.23：0.94，参数取其电池参数按比例抽取，所以p
up
和p
down
取6.75kw，cb取40.5kw
·
h，w取0.182kw
·h·
km-1
。
[0152]
2)初始充放电价及负荷数据
[0153]
实验的历史负荷数据采用pjm美国能源市场某一日内实时负荷数据，电价采用加州电网峰谷分时电价数据，表2、表3分别给出了分时电价的均值和对应当日历史负荷数据。根据目前美国加州私家车保有量623.4万辆，假设模拟加州地区电动汽车接入数量为n＝3
×
106辆计算。
[0154]
表2分时充电电价和实时负荷数据
[0155][0156][0157]
表3初始峰谷充放电价
[0158][0159]
3)用户转移率初始化参数
[0160]
根据用电用户调查情况，将转移率曲线初始值参数设定为如表4所示，并通过每次优化更新用户转移率参数。
[0161]
表4用户转移率初始值参数
[0162]
转移率类型斜率k
ab
死区计算值l
ab
峰平转移率曲线0.060.11峰谷转移率曲线0.080.12平谷转移率曲线0.040.09
[0163]
4)电动汽车用户出行习惯数据分析
[0164]
本专利取电动汽车用户起始出行时间分布fs(t)满足t～n(17.47,3.4122)的正态分布，而电动汽车用户的日行驶里程fd(s)满足足lns～n(3.46,1.1422)的对数正态分布，及起始负荷状态分布soc满足n(0.4,0.12)。并计算第i段行程第j时刻到下一时刻k行驶lkm进行充电或放电的电动汽车数量为：
[0165][0166]
式中：n为当前电动汽车的总数量。
[0167]
行驶在当前j时刻选择对电动汽车进行充放电的时长为
[0168][0169]
根据上述关系，利用蒙特卡洛随机抽取，生成单台电动汽车用户一日内的充放电计划(包括：一日内的行驶里程、起始出行时刻、起始负荷状态soc)，计算单其充放电负荷，叠加规模化的电动汽车充放电负荷曲线。
[0170]
(2)csmoifsa算法验证
[0171]
为测试多目标改进免疫鱼群算法的性能，本文选取zdt测试函数集。zdt测试函数在评价多目标算法时具有较好的分布性与收敛性，选取带有两类目标的两种函数，每个的pareto前沿均已知，且问题的变量数目可以变化，其表达式为：
[0172][0173]
对原多目标人工鱼群算法(multi-objective artificial fish swarm algorithm,moafsa)和提出的csmoifsa最优解之间的收敛性、均匀性和误差比进行定量分析。
[0174]
1)收敛性：世代距离(generational distance，gd)即表示所求解与实际pareto前沿之间的距离，世代距离越小越好，说明所求pareto前沿接近于实际值，gd表示为如式：
[0175][0176]
式中p为所求pareto前沿的数据集合；di为所求解与实际pareto前沿之间的欧式距离。
[0177]
2)均匀性：空间分布量度(spacing，sp)即反应所求pareto前沿解的分布性，若空间分布量度的值越小，说明解的分布性越好，sp表示为如式：
[0178][0179]
式中为所求解与实际pareto前沿之间欧式距离的平均数值。
[0180]
3)误差比(error ratio，er)：即所求数据到最远端解之间占有的比例，误差比的值越小越好，说明所求解与实际解之间变差较小，er表示为如式：
[0181][0182]
式中n为非支配解的个数；ei为二进制变量，当解不在pareto最优前端内为1，解在pareto最优前端内为0。
[0183]
仿真初始化参数设置视野范围visual＝0.5，鱼群规模m＝100，最大迭代次数k＝100，拥挤因子δ＝0.25。由于算法在仿真计算过程中存在随机性，使得模拟结果之间存在偏差，所以在实验仿真的过程中每个计算过程都单独运行30次，并取其平均值，记录运行结果。实验结果如表5、6、7所示。
[0184]
表5 pareto解的收敛性指标数据
[0185]
算法bestworstmeanstdmoafsa0.00020.00300.00170.0013csmoifsa0.00030.00290.00150.0014
[0186]
表6 pareto解的均匀性指标数据
[0187]
算法bestworstmeanstdmoafsa9.2e-040.02030.00780.0044csmoifsa7.13e-050.01810.00610.0031
[0188]
表7 pareto解的误差比指标数据
[0189]
算法bestworstmeanstdmoafsa0.00150.09210.05170.0289csmoifsa0.00100.08110.04250.0259
[0190]
由表5至表7分析可知：两种算法的pareto前沿解收敛性相差不大；csmoifsa算法的均匀性指标值明显优于moafsa算法，其均匀性指标值下降了18.39％；对比误差比指标可知，csmoifsa算法平均误差相较于moafsa算法减少了11.9％。根据上述实验指标分析可知，两种算法在收敛性上相差无几，但csmoifsa算法拥有良好的pareto前沿解分布，并且其误差比更较小，更接近真实值。
[0191]
(3)多目标优化模型求解算例分析
[0192]
实验仿真实现在python3.8平台下，采用csmoifsa对电动汽车充放电价多目标模型进行优化求解，每次优化后根据电动汽车响应与电价关联模型计算新电价下用户的负荷变化情况。节省投入成本与峰谷差随用户满意度变化曲线如图2所示。
[0193]
如图2可知，节省投入成本、峰谷差与运营商、电网公司利益有关，节省投入成本随用户满意度逐渐减少，而峰谷差是随用户满意度增加。当节省投入成本最大、峰谷差最小时将影响用户满意度，在用户满意度65％～85％之间节省投入成本与峰谷差调节程度最大，
因此在这个范围的pareto解使得用户响应电价的能力较高。对比在单一目标下的优化情况，把电网系统峰负荷、峰谷差最小作为优化的共同目标，分别以用户满意度θ最大和运营商投入cost最小化为目标在pareto解集中搜索极端解，结果如表8所示。
[0194]
表8 pareto解集中的极端解
[0195]
优化目标θ/％cost/万美元峰谷差/mw峰负荷/mw用户满意度最大0.922937214436.994775.6运营商成本投入最小0.452903516897.796142.3
[0196]
由表8可知，若仅以用户满意度最大为目标，则会增加运营商的投入成本。若仅以运营商投入最小为目标，则会降低用户的满意度，进而降低其响应电价的能力，使得峰谷差与峰负荷加大。计算两种极端解下不同响应用户的充放电负荷变化情况，其结果如图3、4所示。
[0197]
由图3、图4可知，在只考虑用户满意度最大化下，电动汽车用户根据自己利益进行充放电，使得用户都集中在峰时段与谷时段向电网充放电，增加了峰谷时段对电网充放电的压力；而在运营商投入最小化下，运营商为调节负荷减少峰谷差与成本投入，大幅度调整峰、谷时段电价吸引用户充放电，使得响应充电的用户开始向平时段和谷时段开始转移，响应充放电的用户开始集中在高峰时段放电，导致用户充放电方式大幅度变化，此时的用户满意度较低。
[0198]
因此，为协调综合电网公司、充电站运营商和用户三方利益，在其他目标不为局部劣解的情况下，采用csmoifsa方法保证在pareto解集中搜索最优折衷解，如表9所示。
[0199]
表9最优折衷解
[0200]
优化目标θ/％cost/万美元峰谷差/mw峰负荷/mw多目标优化0.832918316033.595352.1
[0201]
其中在最优折衷解下峰谷充放电价如表10所示：
[0202]
表10最优峰谷充放电价
[0203]
时段充电电价/(美分
·
(kw
·
h)-1)放电电价/(美分
·
(kw
·
h)-1)峰时段38.4940.12平时段9.5215.32谷时段4.419.89
[0204]
根据最优折衷解计算得到电价优化前后日负荷曲线、多目标优化下不同响应用户负荷曲线如图5、图6所示。
[0205]
由图5、图6可知：1)在优化后峰谷充放电价下对比优化前峰负荷减少了1689.24mw，峰谷差下降了3364.2mw。2)优化后峰时段负荷减少，选择充电的用户开始向平时段和谷时段转移，使得系统负荷变化平滑峰谷差缩小。3)响应放电电价用户在系统负荷高峰时段开始向电网放电，缓解了电动汽车接入后对充电负荷的需求，并且响应充电电价的用户在用电低谷和平时段改变自己的充电时刻，减少了高峰时刻充电的压力。
[0206]
综上所述，若在求解充放电价时只保证其中一个目标最优，则将导致其它目标陷入劣解。而在峰谷充放电价多目标优化下，电网公司、充电站运营商和用户三方利益得到协调，在满足电网系统峰负荷、峰谷差最小下，运营商成本投入减少，用户满意度增加，使得更
多的用户参与电价优化。最终实现通过充放电价多目标优化方法引导用户有序充放电，达到“削峰填谷”的目的。