基于非线性退化的轧辊剩余寿命预测实现方法

1.本发明涉及的是一种轧钢生产领域的技术，具体是一种基于核函数-wiener过程的非线性退化的轧辊剩余寿命预测实现方法。


背景技术：

2.轧钢生产线是典型的连续工业生产线，即除了启停和异常情况之外，生产物料以连续状态通过整个生产流程，期间生产设备均处于运转状态。轧辊是轧机的关键部件和大型耗材，其更换冷却及维护操作会打断钢铁的连续生产进程，进而影响轧钢生产线的生产效率和经济效益。针对轧辊失效过程建立退化模型并实现剩余寿命预测，对于钢铁企业降低轧辊磨削损耗、提升轧线生产效率及产品质量具有重要意义。


技术实现要素：

3.本发明针对现有技术需要利用大量的数据对相关模型进行训练才能进行操作，且提供的参考信息有限的缺陷，考虑轧辊退化路径中存在的随机性和非线性特点，提出一种基于非线性退化的轧辊剩余寿命预测实现方法，通过对轧辊剩余寿命进行预测与分析，能够实现对轧钢生产线从当前的定期维护过渡到基于条件的维护，提高轧钢产品质量并降低生产成本。
4.本发明是通过以下技术方案实现的：
5.本发明涉及一种基于非线性退化的轧辊剩余寿命预测实现方法，通过构建基于核函数的非线性wiener过程退化模型并初始化参数后，采用轧辊健康状态历史序列对模型进行训练；在在线阶段采用基于非线性wiener过程退化模型的完整表达式，对待测轧辊退化数据进行计算，得到预测输出及其概率分布，并根据预测输出及其概率分布推导得轧辊剩余寿命的概率密度函数，实现剩余寿命预测。
6.所述方法具体包括：
7.第一步，从更换表单/维修表单收集轧辊直径和轧制公里数等历史数据，并去除无效数据，获得轧辊健康状态历史序列将作为模型的输入数据；
8.第二步，构建非线性wiener过程退化模型；
9.第三步，构建基于核函数的非线性wiener过程退化模型的一般形式；
10.第四步，根据轧辊实测数据选取效果最好的核函数嵌入模型，得到非线性wiener过程退化模型的具体形式；
11.第五步，基于轧辊退化历史数据和贝叶斯公式，推导模型未知参数w和σ的后验分布，获得边际似然函数，并通过最大化边缘似然函数，最终得到参数w和σ的最大似然估计值。
12.第六步，通过迭代估计算法求得非线性wiener过程退化模型的近似解，作为模型参数的估计值，生成非线性wiener过程退化模型的完整表达式；
13.所述的迭代求解，根据核函数性质删除迭代过程中部分权重和核函数，通过此过
程实现模型的稀疏性，提升了工程分析效率以适用轧辊性能状态的在线监测。
14.第七步：基于非线性wiener过程退化模型的完整表达式，对待测轧辊退化数据进行计算，得到预测输出及其概率分布；
15.第八步：基于wiener过程的首达时间服从逆高斯分布这一特性，根据预测输出及其概率分布推导得轧辊剩余寿命的概率密度函数，实现剩余寿命预测。
16.本发明涉及一种实现上述方法的系统，包括：数据预处理单元、模型构建单元、退化建模单元以及剩余寿命预测单元，其中：数据预处理单元根据生产线原始历史数据，进行数据清洗处理，得到模型的输入数据；模型构建单元根据处理完的轧辊实测数据，基于核函数的wiener过程模型，进行贝叶斯参数估计，得到非线性wiener过程退化模型；退化建模单元依据非线性wiener过程退化模型计算得到未来时刻的预测输出及其概率分布，剩余寿命预测单元根据非线性wiener过程退化模型和预测输出及其概率分布，得到轧辊当前剩余寿命的概率密度函数，从而提高设备运转效率与安全性并实现视情维护。技术效果
17.本发明考虑随机过程的同时结合核函数能够捕捉轧辊的复杂非线性退化路径的特点，构建基于核函数的wiener过程退化模型，推导得到的失效分布蕴含首达时的概念，包含了可能失效的概率分布范围，为制定轧辊维修和备件计划提供更具体的决策依据，相较非线性wiener过程和相关向量机算法，本发明在拟合优度上分别提高109％和14％，剩余寿命预测误差小于5％，具有较优秀的建模能力与预测效果。管理人员可以根据建模结果和剩余寿命制定维护计划，并可根据产线压力在预测区间内进行动态调节。
附图说明
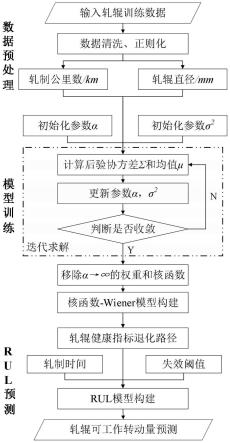
18.图1为本发明流程图；
19.图2和图3为实施例效果示意图。
具体实施方式
20.如图1所示，本实施例结合某钢铁公司1580热轧生产线现场数据，进行基于非线性退化的轧辊剩余寿命预测，具体包括：
21.第一步，从更换表单/维修表达收集有效的轧辊直径和轧制公里数历史数据，并去除无效数据，结合轧辊健康指标获得轧辊的健康状态时间序列。
22.第二步，构建经典非线性wiener过程退化模型x(t)＝ηλ(t)+σb(t)，其中：σb(t)是扩散函数，λ(t)为时间尺度转换函数，常用的为指数函数t
λ
，不适用轧辊的复杂非线性过程，需引入形式更灵活的漂移函数。
23.第三步，引入核函数解决轧辊退化过程中的非线性表征问题，替代经典非线性wiener过程中的漂移函数λ(t)，构建基于核函数的wiener过程退化模型其中：核函数的一般形式为k(t，ti)＝λ(t)
·
λ(ti)，wi是权重系数，w0为截距，ti为i时刻健康状态时间序列的对应值；
24.第四步，根据轧辊实测数据的预测效果选取效果最好的核函数嵌入模型，具体为：使用均方根误差(rmse)预测值与实际值间的均方根误差、用平均绝对误差(mae)表示绝对
误差，其值越小则表明算法预测精度越高、用可决系数(cd)拟合优度，即相关系数的平方；通过对三者(cd的倒数)叠加评价模型的性能，其中：通过对三者(cd的倒数)叠加评价模型的性能，其中：其中：x(t)表示实际值，为模型预测值；
25.表1常用核函数的表达式
26.第五步，基于轧辊退化历史数据和贝叶斯公式，基于核函数-wiener过程退化模型的独立增量为x＝(δx1，
…
，δxn)
t
，其联合概率密度函数服从多元高斯分布，即：，其联合概率密度函数服从多元高斯分布，即：，其联合概率密度函数服从多元高斯分布，即：其中：其中其中∑是元素的协方差矩阵，∑(i，j)＝σ
2 min(ti，tj)；
27.对未知参数w和σ的后验分布进行推导，获得边际似然函数，并通过最大化边缘似然函数，最终得到参数w和σ的最大似然估计值，具体包括：
28.5.1)为避免模型出现过拟合现象，定义参数w的先验分布为均值为0的高斯分布，即：其中α＝(α0，α1，
…
，αn)是w的超参数向量；
29.5.2)定义α和σ2的超先验分布服从gamma分布，即p(β)＝gamma(β|c，d)，a＝b＝c＝d＝10-4
；
30.5.3)基于贝叶斯公式，推导未知参数w、α和σ的后验分布为p(w，α，σ2|x)＝p(w|x，α，σ2)p(α，σ2|x)；
31.5.4)最大化边际似然函数p(α，σ2|x)，使p(x|α，σ2)最大，得：)最大，得：其中其中
32.第六步，通过迭代估计算法对未知参数α和σ2进行近似求解，算法停止迭代后可得模型参数的估计值，具体包括：
33.6.1)推导得α和σ2的迭代更新值分别为和(σ2)
new
＝||x-φμ||2/n-∑iγi，其中：∑＝(σ-2
φ
t
φ+diag(α1，
…
，αn))，μ＝(diag(α1，
…
，αn)+φ
t
∑-1
φ)-1
+φ
t
∑-1
φx；
34.6.2)循环迭代直到达到最大循环次数或者输出结果的梯度小于收敛条件(10-3
)，
并记α
mp
和σ
2mp
为停止迭代后的最优值；
35.6.3)在迭代过程中易发生部分αi趋于无穷的现象，根据核函数性质删除迭代过程中所有αi＞α
max
的αi所对应的权重和核函数，并设α
max
＝105，通过此过程实现退化模型的稀疏性，提升了工程分析效率以适用轧辊性能状态的在线监测。
36.第七步：根据第六步得到的估计值生成退化模型的完整表达式，在在线预测阶段，根据待测轧辊退化数据x
*
，计算轧辊预测值及概率分布，具体为：，计算轧辊预测值及概率分布，具体为：其均值和方差分别为：其均值和方差分别为：其中：α
mp
和为第六步停止迭代后参数的最优值。
37.第八步：将待测轧辊退化数据θ
1:n
＝{θ1，θ2，θ3，...，θn}作为输入，结合第六、第七步推导得到的轧辊剩余寿命的概率密度函数为其中：ξ为预设失效阈值。
38.基于第八步获得轧辊在任意时刻的剩余寿命预测值及其分布，可为确定轧辊更换周期和磨削量提供技术支撑和决策依据，进而提高产品质量和轧辊使用寿命，降低停机损失。
39.经过具体实际实验，在某钢铁厂1580生产线实测数据下，根据表2的实验结果，选择gaussian核函数。
40.表2核函数rmsecdmaegaussian核函数1109.80.9893865.1多项式核函数7713.10.47815916.9线性核函数10717.10.00007589.3laplace核函数2046.50.86641475.4sigmoid核函数10717.00.00007589.3
41.运行上述方法，以120批次时预测剩余寿命为例，由第八步推导剩余寿命的概率分布如图2蓝部分所示。预计下线批次为141批次，包含了可能失效的概率分布范围，推导得剩余寿命的5、50和95个百分位分别为16、21和26，可为制定轧辊维修和备件计划提供更具体的决策依据。例如，若管理人员采取较保守的维护策略，可在接近16批次后进行更换维修，若管理人员结合生产压力采取较为激进的维护策略，可在接近26批次后再进行更换维护操作。
42.与现有技术相比，表3中提供了基于核函数-wiener过程的轧辊非线性退化建模与常见建模方法的效果对比，能够得到的实验数据如表3所示。
43.表3模型rmsecdmae基于高斯核函数的wiener过程模型1109.70.9893865.1指数wiener过程模型8059.80.47266369.4基于高斯核函数的相关向量机模型1992.70.87191591.2
44.三种模型建模效果如图3所示，可以直观看出本发明的性能具有明显提升。
45.如表4所示，为基于核函数-wiener过程的轧辊非线性退化建模的寿命预测平均误
差统计。
46.表4时间序列rul预测值rul实际值误差no.8053790.556537.74.9％no.10052630.252021.61.2％no.12040764.137671.38.2％
47.上述具体实施可由本领域技术人员在不背离本发明原理和宗旨的前提下以不同的方式对其进行局部调整，本发明的保护范围以权利要求书为准且不由上述具体实施所限，在其范围内的各个实现方案均受本发明之约束。