一种基于拉格朗日原理的需求响应式BRT车辆调度算法

本发明属于智能优化调度、路径规划，具体涉及一种基于拉格朗日原理的需求响应式brt(bus rapid transit巴士快速公交系统)车辆调度算法。

背景技术：

1、随着社会经济的飞速发展和城市化进程的加快，城市机动车保有量迅猛増长，交通拥堵与交通碳排放问题日益严峻。研究指出，实现居民出行方式向公共交通方式转移是缓解上述负面影响、促进城市可持续发展的主要途径。但传统公共交通存在到站准点率低、行驶速度慢、候车时间长、高峰时段车厢拥挤等诸多问题，在与私人交通方式的竞争中处于劣势，因此，迫切需要传统城市公交不断创新发展，以提供高品质、高效率、高智能的服务。“需求响应式brt”(也称为智慧车列交通系统)是近年来国内学者提出的一种创新的公共交通模式，并已在上海市和深圳市开通了示范线进行实地测试。系统定位于创建大规模出行、智能共享出行、绿色环保、安全高效的新一代城市骨干交通方案，是解决大城市病、建设绿色城市、智能城市的有效路径。

2、需求响应式brt(bus rapid transit巴士快速公交系统)中多种容量的自动驾驶车辆通过无线通信技术v2x编组形成车队进行服务，车辆在运行中根据需要在不同车队间并入或脱离，可提供灵活的运量以适应不同强度下的运输需求；乘客通过手机软件实时预约出行，无需在站台等待，从而实现精准候车、人人有座的高质量服务；基于预约信息，系统筛选起讫和出发时间相同的乘客构成“需求组合”，同一组合的乘客通过集约化的拼车方式由车队一同运送，该方式突破了传统公共交通“站站停”的组织模式，可实现“点到点”的快速运送；系统设置专用车道并实行交叉口信号优先策略，避免社会车辆干扰，保证运行安全高效。

3、但同时，这种需求响应的实时性、与需求量相适应的车辆编组、点对点直达服务导致的供需不平衡等问题也对系统的车辆调度提出了巨大挑战，现有公共交通(如地铁等)的调度方法不适用于这一交通系统。车辆调度是系统实现高效可靠运营的重要保障，因此如何考虑需求响应式brt的上述运营特点和约束对该系统车辆进行实时动态的调度优化是需要解决的关键问题，也是目前实现系统落地投入运营亟待攻克的技术难点。

技术实现思路

1、发明目的：针对近年国内学者提出的新兴公共交通系统——需求响应式brt(也称为智慧车列交通系统)，提出一种基于拉格朗日原理的车辆调度算法，通过求得合理的车辆调度方案来最大化运营收益，使得系统运行安全有序，提升系统的竞争力。同时，也对该系统尽快落地投入运营起到积极的推动作用。

2、为实现上述目的，本发明采用如下技术方案：

3、一种基于拉格朗日原理的需求响应式brt车辆调度算法，包括以下步骤：

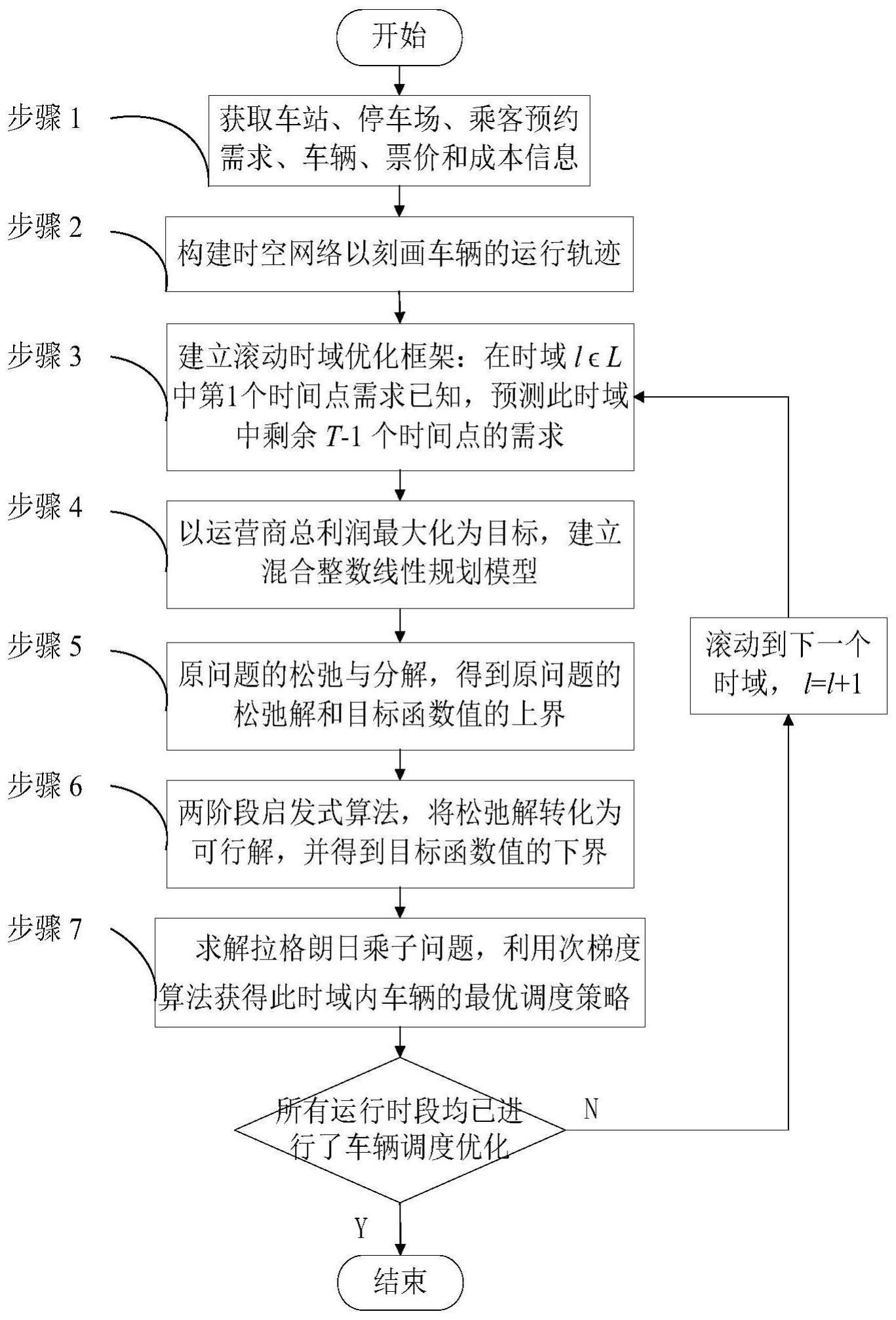
4、步骤1：获取车站、停车场、乘客预约需求、车辆、票价和成本信息。

5、所述车站信息包括各车站位置；所述停车场信息包括各停车场位置、停车位数量；所述乘客预约需求信息包括各乘客出发时间、出发站点和到达站点；所述车辆信息包括车型、各车型车辆数、车速、车辆初始分布；所述票价和成本信息包括票价、运行成本、停车成本。

6、步骤2：根据系统运营中可能存在的车辆状态和活动，构建时空网络以刻画车辆的运行轨迹。

7、具体为：

8、时空网络(v,a)中，网络的空间维度包括车站和停车场，时间维度被离散为一系列等间隔的时间点，表示为t＝{t0,t0+δ,t0+2δ,…}，其中t0为初始时刻，δ为时间间隔，假设所有事件(如车辆出发)均在这些时间点发生。因此，时空节点集合v表征车辆的时间与空间信息，时空边a连接两个时空节点，表征车辆活动。网络中存在以下三种时空边，

9、等待边a1：车辆在停车场停车，等候时间为一个时间间隔δ；

10、服务边a2：车辆将乘客由出发站点运送至目的站点。

11、空调边(全称：空车调度边)a3：空车由需求少的站点调度到需求多的站点。

12、步骤3：建立滚动时域优化框架，以决定每次优化中需求预测和调度决策的覆盖时间，使系统能够响应实时需求而不占用过多的计算资源。

13、具体为：

14、系统采用实时线上预约的方式进行服务，且系统有灵活的预约机制，乘客最晚可以在出行前一个时间间隔δ(例如10min)提交预约需求。故乘客的出行需求具有动态随机性，且随着时间推移逐步出现，无法提前获取一天的完整需求信息集。为实时、快速的响应乘客预约需求，采用滚动时域框架来进行优化。该框架将运行时间划分为|l|个时域，每个时域离散为|t|个时间点。

15、步骤3-1：在时域l∈l中，仅第1个时间点t∈t的需求已知(乘客需要至少提前一个时间间隔进行预约)，所以为提高调度方案的全局性能，根据历史需求数据预测此时域中剩余t-1个时间点的需求。

16、步骤3-2：采用本发明提出的数学模型和算法优化此时域内t个时间点的车辆调度。其中，对于输出的最优解，只保留时域内第1个时间点t∈t的调度策略，而基于预测需求得到的其他t-1个时间点的调度策略是为了帮助系统在时间点t做出更优的决策。

17、步骤3-3：经过一个时间间隔δ后，时间点t+1的需求可完全获得。系统滚动到下一个时域l+1∈l，重复步骤3-1至3-3，直至整个运行时间内的车辆调度优化全部完成。

18、步骤4：在滚动时域优化框架下，基于时空网络以运营商总利润最大化为目标建立混合线性整数规划模型，以后续优化需求响应式巴士快速公交系统的车辆调度问题。

19、具体为：

20、步骤4-1：定义数学规划模型中集合、参数和变量。

21、集合：h为车辆集合，h＝{h}；n为车型集合，n＝{n}；i为站点集合，包括车站和停车场，i＝{i,j}；i1为车站集合，i2为停车场集合，t为当前优化时域中的时间集合，t＝{t,s}；v为时空节点集合，v＝{(i,t),(j,s)}；(id,td)为虚拟时空节点，a为时空边集合，a＝{(i,t,j,s)}，表示车辆t∈t时刻从i∈i站点出发，s∈t时刻到达j∈i站点；

22、参数：为优化时域开始时，位于时空节点(i,t)∈v处的n∈n车型车辆数(表征一个优化时域初始时刻各车辆的位置)；ditjs为时空边(i,t,j,s)∈a上的乘客预约总数，即一个“需求组合”中的出行需求量；en为车型n∈n的座位数；为停车场i∈i中，车型n∈n的停车位数量；为n∈n车型车辆从站点i∈i出发到达站点j∈i的运行成本；为n∈n车型车辆在停车场i∈i等待一个时间间隔的停车成本；pij为乘客从站点i∈i出发到达站点j∈i的票价；cl为总运行成本，为所有车辆运行成本之和；cp为总停车成本，为所有车辆停车成本之和；p为总收益，为所有乘客支付的票价之和；

23、变量：为时空边(i,t,j,s)∈a上n∈n车型车流量，非负整数变量；d′itjs为时空边(i,t,j,s)∈a上可满足的乘客需求量，非负整数变量(可松弛为非负实数变量)。

24、步骤4-2：数学规划模型：

25、max p-cl-cp (1)

26、其中，

27、

28、

29、

30、

31、

32、

33、

34、

35、目标函数(1)由三部分构成：服务乘客所获得的收益、车辆行驶所需的运营成本(汽油消耗和车辆折旧等)以及停车成本。目标是使运营商总利润最大化，其中，总利润等于车票收益减去运营成本和停车成本。

36、式(2)和(3)分别为车站和停车场的车辆流平衡，即每种车型进入站点的车辆数和驶出站点的车辆数应保持平衡。在优化过程中引入虚拟时空节点以保证行程的连通性。由于车辆不允许在车站停留，因此等待边不与车站时空节点相连。

37、式(4)和(5)为需求满足约束，系统提供的座位数必须不小于可满足的乘客需求量d′itjs。同时，d′itjs不应超过乘客总预约出行需求量。

38、式(6)为停车场容量限制，在一个停车场中等待的n车型车辆数应小于该停车场对n车型车辆的容纳能力。

39、式(7)和(8)表示决策变量的类型，和d′it js均为非负整数变量。其中，d′itjs可在不损失任何信息的情况下松弛为非负实数变量。

40、步骤5：原问题的松弛与分解：将数学模型中的难约束松弛到目标函数中，并进一步将原问题分解为两个子问题，使其可以分别通过精确算法高效求解。通过求解松弛问题，得到了原问题的松弛解和目标函数值的上界。

41、具体为：

42、步骤5-1：模型松弛：考虑到约束(4)和(6)较难求解，我们引入拉格朗日乘子λitjs(λitjs≥0,(i,t,j,s)∈a)和将这两组约束松弛到目标函数中，得到原问题的广义拉格朗日函数：

43、

44、满足约束(2)，(3)，(5)，(7)和(8)。

45、步骤5-2：模型分解：松弛约束后变量和d′itjs解除了相互制约关系，使得松弛问题可以分解为以下两个独立的子问题。

46、子问题1：最小费用路径问题

47、从松弛问题中提取变量相关部分形成子问题1，并转化为最小化问题如下：

48、

49、满足约束(2)，(3)和(7)。

50、变量的系数可用广义成本表示，对于服务边和空调边对于等待边公式第三部分为定值。此外，对于初始位置不同、类型不同的车辆其优化问题相互独立，可进一步分解为|i|×|t|×|n|个子问题：

51、

52、满足约束(2)，(3)和(7)。

53、该模型为最小费用路径问题，可采用标号纠正算法求解。

54、子问题2：单变量线性规划问题

55、从松弛问题中提取变量d′itjs相关部分形成子问题2，具体如下:

56、

57、满足约束(5)和(8)。

58、对于不同时空边(i,t,j,s)∈a优化问题相互独立，可进一步分解为|a|个子问题：

59、ωitjs(λ):max(pij-λitjs)d′itjs (13)

60、满足约束(5)和(8)。

61、此问题为简单的单变量线性规划问题。当pij-λitjs≥0时，目标函数(13)为单调递增函数，最优解反之为单调递减函数，最优解

62、步骤5-3：松弛问题最优解和最优值：通过求解子问题1和2，得到松弛问题的最优解和则目标函数(9)可计算如下。由算法对偶性可知，目标函数值w(λ,ξ)为原问题最优值的上界。

63、

64、步骤6：设计两阶段启发式算法以将松弛解转化为可行解，并得到原问题目标函数值的下界。

65、具体为：

66、由于两个子问题都仅考虑了部分约束条件，步骤5得到的松弛解相对于原问题可能是不可行的。为此，设计了一种两阶段启发式算法以将松弛解调整为可行解。

67、步骤6-1：阶段1：根据松弛解调度部分车辆

68、为充分考虑松弛问题的解，我们在保证车辆利用率的前提下尽可能多的分配车辆按照子问题1中得到的路线行驶。同时，对车辆路线进行适当调整，以覆盖更多的高利润需求。假设在一个优化时域的初始时刻，位于时空节点(u,v)∈v处的n∈n车型车辆集合为该车辆集合在松弛解中相应的最优路线为其中，路线上有乘客需求的边用集合表示。

69、步骤6-1-1：在阶段1中，对于一条松弛路线我们仅指派对应集合hnuv中的车辆为其服务，并通过标号纠正算法优化此车辆的路线。当中任意一条边上的需求完全得到满足或集合hnuv中所有车辆都已分配，则此路线优化完毕。接着，选取下一条松弛路线重复上述步骤。

70、步骤6-1-2：时空网络中各边的权重设置如下：对于目前无乘客需求的时空边，权值等于运行成本或停车成本；对于有待满足需求的时空边，如果其在集合中，则赋予较低的权值——运营成本-收益×2，以保持松弛路线，如果不在集合中则赋权重——运营成本-收益，以优化路线捕获更多的高利润乘客。

71、步骤6-1-3：在完成一辆车的调度后，待满足需求的数量，未分配的车辆，剩余的停车位等参数应立即更新。如果某停车场没有可用停车位，则对应的等待边的权值为m(m为一个足够大的常数)。

72、步骤6-2：阶段2：剩余车辆的调度

73、第一阶段完成了部分车辆的调度，但一条松弛路线上仅指派一种类型车辆。因此，在第二阶段，我们将不同类型车辆进行组合来提供服务。阶段2的优化过程与阶段1相似，其中两处差别如下。首先，与阶段1依据松弛解中路线-车辆对应关系进行车辆选择的方式不同，阶段2从剩余车辆中任意选择车辆进行调度。这种随机的方式可以帮助不同容量的车辆组成与需求量相适应的车队，此外，如果所有车辆都已分配完毕或所有乘客预约需求都已满足，则算法终止。

74、步骤6-3：应用两阶段启发式算法，可以得到可行解和将可行解带入目标函数(1)即得到原问题的下界。

75、步骤7：求解拉格朗日乘子问题：利用次梯度算法不断更新拉格朗日乘子，以通过迭代的方式将目标函数值上界和下界之间的差距最小化为零或一个小的可容忍值，最终得到最优解，获得系统中车辆的最优调度策略。

76、具体为：

77、步骤5和6分别得到了最优值的上界和下界。上下界的相对差值gap应最小化到0或一个较小值，以获得质量较高的精确解。这是一个拉格朗日乘子问题，通常用次梯度算法求解。

78、引入k表示算法的迭代次数。则k+1次迭代中拉格朗日乘子可通过以下公式更新：

79、

80、

81、其中，步长θk更新的计算公式如下：

82、

83、其中ubk和lbk表示目前最优的上下界，τk是步长调整参数。

84、拉格朗日乘子λitjs和的初始值通常设为0，gap通过公式(18)计算。

85、

86、与现有技术相比，本发明主要包括以下优点：

87、本发明提出了一种基于拉格朗日原理的车辆调度算法，以解决“需求响应式brt”这一公共交通系统的车辆调度问题。该算法充分考虑了系统运营特点，能够得到与需求量相适应的车辆编组，并解决点对点直达服务导致的供需不平衡等问题。算法可在较短的时间内得到调度问题的精确解，使系统能够响应实时需求而不占用过多的计算资源。本发明可求解得到最大化运营收益的车辆调度方案，使得系统运行安全有序，提升系统的竞争力。同时，也对“需求响应式brt”尽快落地投入运营起到积极的推动作用。