结构健康监测中的大规模结构系统非确定性辨识通用方法

1.本发明涉及结构检测与健康监测技术领域，具体为结构健康监测中的大规模结构系统非确定性辨识通用方法。


背景技术：

2.在结构健康监测领域中，通常需要依赖结构模型开展响应预测、振动控制以及损伤识别与状态评估等相关研究，其中一个重要前提是该模型能准确刻画待监测结构对象的静动力学特性。但待监测结构对象的数学模型往往未知，这就需要利用机理分析建立待监测对象的结构模型，再利用系统辨识确定该结构模型的各种参数。以土木工程结构为例，部署结构健康监测系统通常需要依据结构分析理论并结合原始设计资料等建立待监测结构系统的有限元模型。但由于真实结构的几何材料属性与边界条件等同有限元模型理论假设不可避免地存在偏差，加之长期服役所引起的材料性能劣化等对于结构模型参数产生的未知影响等，导致无法获知待监测结构系统的准确模型。因此，部署结构健康监测系统还需要进一步以该初始有限元模型为基础开展结构系统辨识，在掌握和分析结构系统观测数据的基础上，通过参数识别过程提取结构系统模型的关键特征。
3.从广义角度讲，结构健康监测动力学问题通常包含激励输入、结构系统和响应输出三要素。结构系统识别本质上就是探究输入、系统和输出三者之间的内在规律，找出能够表征系统的特征参数以实现系统识别。此三者关系构成了动力学分析的三个方面，即动力响应分析、系统辨识与荷载预测，其分别对应结构动力学正问题以及第一类与第二类反问题，而反问题解通常是非唯一的，其迭代求解难度远比正问题大得多。另一方面，随着经济社会的迅速发展和科学技术的全面进步，传统的土木工程结构朝着大型化、柔性化和复杂化方向不断发展，超高层建筑与大跨度桥梁等大型土木工程结构不断涌现，在结构健康监测系统的部署中，其相关动力学反问题处理客观上造就了对大规模甚至超大规模结构系统辨识问题有效求解的迫切需求。同时，受实际测量噪声与测量信息不完备以及结构系统模型误差等因素综合影响，结构系统辨识过程及其结果客观上存在不确定性，进一步显著增加了结构系统辨识的难度。因此，有效开展大规模结构系统参数非确定性辨识方法研究，可为大型土木工程结构健康监测系统的有效部署提供关键支撑。
4.结构健康监测中的结构系统辨识问题求解通常需要预先设计合理的损失函数，以量化实际观测数据与结构系统模型预测之间的差异，将系统辨识问题转换为数值优化问题，再选用适当的优化算法加以解算，以实现结构系统参数辨识。但是，通常所采用的损失函数直接极小化方法在实测数据量相对于系统参数规模较小的情况下极易产生过拟合问题，其对系统辨识的噪声鲁棒性以及辨识模型的泛化能力影响很大。应对该问题最常用的方法就是引入正则化(doi:10.3321/j.issn:1671-4431.2005.02.027、doi:10.3969/j.issn.1671-5942.2009.02.029、cn114998750a、cn114581553a、cn111795742a)，降低模型复杂度并收缩解空间，但是目前广泛采用的正则化方法大都为确定性的，无法考虑非确定性因素影响。从贝叶斯观点来看，正则化项本质上属于一种先验信息，因而在贝叶斯推断框
架内包含正则化的系统辨识可视作一种以损失函数为似然函数的贝叶斯最大后验估计，以此为基础可实现系统辨识的非确定性量化评估，而正则化超参数的合理取值对系统辨识影响极大(cn111795742a)。尽管在贝叶斯推断框架基础上可进一步实现正则化超参数推断，然而，大规模结构系统辨识中负对数后验的高维黑塞矩阵的反复计算将非常耗时，严重阻碍了其在大型结构健康监测系统辨识中的实际应用.
5.基于贝叶斯推断的系统辨识问题可以采用非线性最小二乘方法进行解算，当前，lm算法与信赖域算法是最常用的两种非线性最小二乘求解方法(doi:10.1098/rsos.171226、doi:10.13272/j.issn.1671-251x.17321、doi:10.7652/xjtuxb202004002、cn109855652a)，其高斯-牛顿逼近能显著降低高维黑塞矩阵的计算量，以期有效提升大规模系统辨识效率。然而，常规lm算法的局限性在于其无法处理边界约束问题，而适当的边界约束对于结构系统辨识通常是必要的，其通过限定系统参数的调整范围，确保辨识结果的合理性。鉴于此，目前基于常规lm算法的非线性最小二乘在贝叶斯正则化上的应用均未考虑边界约束条件(doi:10.1016/j.ymssp.2018.05.024、cn109855652a)。而另一方面，信赖域算法虽然可以处理边界约束情况，但是该方法的劣势在于其无法解决欠定性问题(doi:10.1098/rsos.171226)，而该欠定性问题在结构系统辨识中通常难以避免，其会导致辨识过程病态，尤其是面对少量测量信息与大规模待辨识参数集的实际情况时，该信息不完整与非对称性所导致的病态问题将愈加严重。此外，由于非线性最小二乘方法最初并不是专门针对贝叶斯推断问题而提出的，因而将非线性最小二乘方法用于贝叶斯正则化超参数推断问题需要深入解读相关算法的源代码，并对源代码进行定向修改以及重新编译。然而，该过程并非易事，一方面是因为详尽解读相关算法的源代码不仅需要使用者具备专门的数值优化背景理论并熟稔相关程序语言及编程技巧，而且程序定向修改与调试校验工作本身繁琐并容易出错。另一个关键方面是面对大规模系统辨识问题的求解需求，必须确保所采用非线性最小二乘方法的高效性与可靠性，而同时兼具这两方面特性的大都是成熟的闭源程序，这就导致无法通过源代码定向修改以有效利用成熟闭源代码在大规模甚至超大规模数值优化问题解算上的强大优势。


技术实现要素：

6.本发明的目的在于提供结构健康监测中的大规模结构系统非确定性辨识通用方法，以解决上述背景技术中提出的问题。
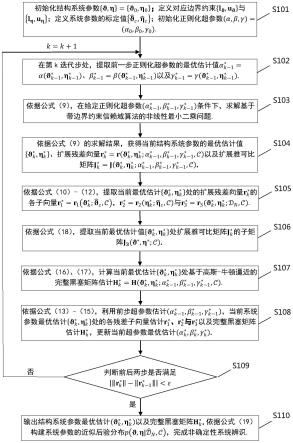
7.为实现上述目的，包括以下步骤：步骤一，初始化结构系统参数与正则化超参数：首先依据设计图纸资料建立目标结构系统初始模型，确定系统模型参数化方案并予以初始化再确定系统参数的标定值若当前无标定值，则赋予相应的名义值；接着定义适当边界约束条件{i
θ
，u
θ
}与{l
η
，u
η
}，确保辨识结果的合理性；然后初始化各正则化超参数值(α，β，γ)＝(α0，β0，γ0)与迭代次数累积计数器k；步骤二，提取各正则化超参数的估计值：假设当前处于第k轮迭代，提取第k-1轮中获得的各正则化超参数最优估计值值以及为当前迭代步所开展的非线性最小二乘辨识提供重要基础参数；步骤三，求解约束非线性最小二乘问题：利用前步正则化超参数的最优估计值
求解基于信赖域算法且考虑边界约束的非线性最小二乘问题，并合理控制非线性最小二乘算法的收敛条件，使其不宜过分苛刻，既可节省单轮计算时间，也使系统参数在本轮获得适度调整，能有效避免单次调整步长过大可能导致的总体收敛困难；步骤四，输出约束非线性最小二乘求解结果：依据约束非线性最小二乘在给定正则化超参数条件下的求解结果，获取本轮结构系统参数的最优估计值同时包括经本技术扩展的残差向量以及对应的扩展雅可比矩阵步骤五，提取扩展残差向量的各子向量：在当前结构系统参数最优估计条件下，从扩展残差向量中分别提取各子向量估计中分别提取各子向量估计与为后面执行的各正则化超参数更新提供基础；步骤六，提取原始残差向量的雅可比矩阵：在当前结构系统参数最优估计条件下，从扩展的雅可比矩阵中提取与原始损失函数残差向量对应的子雅可比矩阵步骤七，估算结构系统参数的黑塞矩阵：在当前结构系统参数最优估计条件下，基于非线性最小二乘框架内的高斯-牛顿逼近理论，利用前面获得的雅可比矩阵并结合各正则化超参数估计对完整黑塞矩阵进行估算；步骤八，更新当前迭代步的正则化超参数：在前轮中各正则化超参数估计值基础上，联合当前系统参数最优估计下扩展残差向量的各子向量与以及完整黑塞矩阵估计更新并获得当前超参数的最优估计步骤九，进行总体迭代收敛性判定：判断前后两轮中的扩展残差向量模与的差别是否满足收敛条件，即其差的绝对值是否小于一个给定值ε；若成立，则判定总体迭代收敛，并输出相关结果；否则，更新迭代计数器，k＝k+1，并重新从第(s102)步开始执行；步骤十，输出系统参数最优估计及其概率分布：若判定总体迭代获得收敛，则输出结构系统参数最优估计以及完整黑塞矩阵构建结构系统参数的近似后验概率分布从而实现大规模结构系统参数的非确定性辨识。
8.作为本发明的一种优选技术方案，健康监测结构系统的输出概率分布符合以下多元高斯分布形式其中函数用来描述结构系统的输入输出关系，其接受系统输入向量(如外部激励)，并给出系统输出向量(如各类静动力学响应)；ni和no分别表示系统输入和输出向量维度；符号表示多元高斯分布形式；超参数γ表示每个预测误差分量高斯分布的精度或逆方差；和分别代表不同类型的结构系统参数组，其维度分别通过n
θ
和n
η
定量表征；表示由该两组参数θ和η所具体描述的一
类模型。
9.作为本发明的一种优选技术方案，将两组结构系统参数一般性地推广至任意多组参数的情况。获取了n组相互独立的观测数据{x
(n)
，t
(n)
}，n＝1，2，
…
，n，该观测数据集合由下列公式定义。因此，在给定模型类和数据集情况下，基于公式(1)的似然函数可以表示为：其中，||
·
||表示向量的欧几里德范数。
10.作为本发明的一种优选技术方案，结构系统参数组θ和η的先验分布分别服从以下高斯分布，即即其中，和分别表示此前阶段通过结构健康监测系统辨识获得的参数标定值。若此前无标定结果，则可以依据结构原始设计图纸资料取为各参数组的名义值。正则化超参数α和β分别代表预测误差高斯分布的逆方差。和分别表示维度为n
θ
和n
η
的1向量。基于此前给出的似然函数以及先验分布，在贝叶斯框架内可获得结构系统参数组的后验分布为：其中，重新定义的广义数据集将实测数据信息与系统参数的标定信息合并考虑，并给出如下，公式(6)中结构系统参数组后验分布的分母称为证据，由以下关于参数组的多重边缘积分所给出，即在贝叶斯理论框架内，在构造拉普拉斯积分的渐近展开基础上，该证据因子可以进一步实现最优模型类推断这一项关键内容，即在信息理论框架内获得满足模型参数化复杂度与其信息论复杂度之间相对平衡条件的结构系统最优参数化表征，基于该最优系统模
型类表征，有望进一步提升本技术应用于结构系统辨识的效率和准确度。
11.作为本发明的一种优选技术方案，依据最大后验估计定义，结构系统参数组的最优估计值{θ
*
，η
*
}可以通过极大化公式(6)中的后验分布的对数予以实现，而本技术将其转换为如下扩展的非线性最小二乘形式，即其中，表示经本技术扩展后的整体残差向量。和分别表示与各超参数相关的扩展子向量，而则代表与原始损失函数对应的残差向量，并且此三者可以直接从扩展后的整体残差向量中提取，其分别表示如下：其分别表示如下：其分别表示如下：从公式(9)中可以明显看出，本技术基于正则化超参数向量r1和r2对原始残差向量r3进行了有效扩展，构建了扩展后的整体残差向量r。很明显，扩展后残差向量的维数nr＝n
θ+nη
+nno恒大于结构系统的参数总数n
θ+nη
，这就使得无论结构系统的参数化表征规模大小如何，在本技术框架内，其系统辨识问题的超定性将获得恒满足，而不受实测信息的欠完整性与非对称性影响，从而也自然使得带边界约束的非线性最小二乘方法可以在本技术中得到有效应用。
12.作为本发明的一种优选技术方案，在获得结构系统参数的最优估计值{θ
*
，η
*
}的基础上，经推导，各正则化超参数可以分别通过以下隐式表达式进行更新，即即即其中，表示关于系统参数组的黑塞矩阵，其由下式给出：其中，操作符tr(
·
)与bd(
·
)分别表示矩阵求迹运算与分块对角矩阵运算。与分别表示n
θ
×nθ
维零矩阵与单位矩阵，同理，与分别代表n
η
×nη
维零矩阵与单位矩阵。表示原始损失函数在最优估计值(θ
*
，η
*
}处的黑塞矩
阵，其在非线性最小二乘理论框架内可以很方便地通过下式逼近获得：其中，表示原始残差向量相对于结构系统参数组的雅可比矩阵，其在本技术框架内可以通过非线性最二小乘理论框架所输出的扩展雅可比矩阵直接提取得到，即因此，基于结构系统参数最优估计值{θ
*
，η
*
}与正则化超参数最优估计值(α
*
，β
*
，γ
*
)处的黑塞矩阵估计可以近似构造结构系统参数的后验概率分布如下：
13.作为本发明的一种优选技术方案，求解基于信赖域算法且考虑边界约束的非线性最小二乘问题基于公式(9)；提取扩展残差向量的各子向量时依据公式(10)-(12)；提取原始残差向量的雅可比矩阵时依据公式(18)；估算结构系统参数的黑塞矩阵时依据公式(16)和(17)；更新当前迭代步的正则化超参数时依据公式(13)-(15)；构建结构系统参数的近似后验概率分布时依据公式(19)。
14.与现有技术相比，本发明的有益效果是：1，本技术无需对非线性最小二乘代码作任何修改：本技术采用基于带边界约束的非线性最小二乘方法解算大规模结构系统非确定性辨识的贝叶斯正则化推断问题，此过程无需对算法源代码作任何定向设计或局部修改，完全可以将稳定、可靠的闭源程序直接当作黑箱使用，能有效利用并充分发挥成熟高效算法的强大求解能力以及在大规模结构系统辨识问题上的应用效率。2，本技术仅需要对目标函数向量进行简单扩展：本技术基于贝叶斯推断框架，利用包含各正则化超参数的若干向量对原始损失函数残差向量进行扩展，使扩展后的组合目标函数向量在维度上恒满足大规模结构系统辨识问题的超定条件，可自然满足考虑边界约束下基于信赖域算法的非性线最小二乘方法的适用条件，也能进一步有效解决大规模系统辨识中由于实测信息不完备与非对称所导致的严重病态问题。3，本技术广泛适用于求解各类系统辨识反问题：本技术思路可以一般性地适用于结构健康监测系统辨识中各类反问题的非确定性解算，只需要在贝叶斯理论框架内针对特定问题的正则化先验信息项进行适当的推演，以确定包含各正则化超参数扩展向量的具体形式，而无需对非线性最小二乘代码作任何修改，即可以广泛应用于结构模型参数识别、外荷载预测以及结构模型参数与外荷载联合反演等动力学反问题。4，本技术可通过有限差分的并行化大幅提升效率：本技术可以充分利用有限差分算法的并行化计算策略，大幅提升大规模甚至超大规模雅可比矩阵的计算效率，进一步充分发挥黑塞矩阵的高斯-牛顿逼近的强大计算优势，从而显著提高大型结构健康监测中的大规模结构系统非确定性辨识效率。
附图说明
15.图1为本发明主要计算流程图；
16.图2为本发明大跨度悬索桥结构模型及其测量点布置示意图；
17.图3为本发明索桥大规模结构系统模型参数的迭代历程曲线示意图；
18.图4为本发明索桥结构系统模型参数的首轮迭代是以及收敛时的非确定性辨识结果
具体实施方式
19.实施例1
20.如图1至图4所示，本发明公开了结构健康监测中的大规模结构系统非确定性辨识通用方法，将图1的计算流程应用于图2所示的大跨度悬索桥大规模结构模型的健康监测。应指出，吊索作为此类缆索承重体系大跨度桥梁的关键传力构件，将桥面加劲梁自重、外荷载传递到主缆，其健康状态对于桥梁整体结构安全起着决定性作用，因此，本应用例将对所有吊索健康服役状况进行有效监测与评估。先将本悬索桥模型所有吊索进行有效分组，具体将上下游同一断面上的每对吊索分成一组，全桥共33组吊索。再将各组吊索的健康状态通过其弹性模量来进行表征，并相应通过33个无量纲比例系数来对每组吊索的弹性模量即健康状态进行量化。然后，利用健康监测数据采集系统所获得的动力特性参数数据对反映吊索组健康状态的所有无量纲参数进行反演，从而实现其健康评估。图1中的圆圈表示健康监测系统桥面传感器的布设方案，共36个位置，其中，每个位置均考虑桥面侧向与竖向两个测量方向，即共72个测量方向，如各测点箭头所示。同时，假定基于采集动态响应数据分析获得该悬索桥桥面的10阶模态参数，其包括自振频率和对应模态振型，并进一步利用这些模态参数数据，实施对该大跨度悬索桥吊索的健康状态监测评估。
21.本应用例实施的计算机平台配置为windows10 64位专业版操作系统，amd r9 5950x处理器，128g内存，512g固态硬盘；数值计算软件平台为matlab r2021a，基于该数值编程环境实现本技术的程序编制，并利用该环境下的sdtools专业工具箱搭建以该悬索桥所有吊索组为待辨识参数的大型结构系统模型，同时以黑箱形式将matlab数值平台内置的基于信赖域算法且考虑边界约束的非线性最小二乘算法嵌入本技术程序，即仅依赖于该内置标准算法的输入输出接口参数与本技术方法进行信息交互。对所定义的全部33组吊索弹模无量纲标定参数名义值中添加20％的随机摄动(即，ones(33，1)+0.2
×
randn(33，1))，以模拟其长期服役期间吊索健康状态参数发生未知改变；同时，基于摄动后的所有吊索参数组执行正向计算并考虑噪声，获取相应的模态参数模拟实测值；在此基础上，将原始损失函数定义为各阶自振频率与模态振型的模拟实测值与结构系统模型计算值之间的差异，初始化各类参数(其中，结构系统模型参数初值{θ0，η0}＝ones(33，1)，边界约束条件分别为：下边界{i
θ
，l
η
}＝0.1
×
ones(33，1)、上边界{u
θ
，u
η
}＝2
×
ones(33，1)，以及各正则化超参数初值(α0，β0，γ0)＝(1，1，1))，并执行本技术框架以实现全部33组吊索的健康状态表征参数辨识。
22.图3表示该大跨度悬索桥结构系统模型参数的迭代历程曲线，从图中可以很明显地看到所有模型参数的收敛均很迅速，都能很快地趋近真实值，这表明本技术在大规模模型辨识中的高效性。为了进一步体现本技术的非确定性辨识能力，图4表示该悬索桥结构系统模型参数的非确定性辨识结果。其中，图4(a)表示本技术首轮迭代时的非确定性辨识结果，而图4(b)表示本技术收敛时的非确定性辨识结果。对比两图中的结果，可以很明显地看
出，迭代开始之初，结构系统模型参数的不确定性很大，同时模型参数估计值相对于真实值的误差也很明显。相比之下，随着迭代进行，系统参数估计值的不确定性逐渐降低，且准确性相应提高，直至收敛。这充分验证了本技术在大型结构系统的大规模模型非确定性辨识中的可行性与有效性。
20.上述虽然对本发明的具体实施例作了详细说明，但是本发明并不限于上述实施例，在本领域普通技术人员所具备的知识范围内，还可以在不脱离本发明宗旨的前提下做出各种变化，而不具备创造性劳动的修改或变形仍在本发明的保护范围以内。