一种病态问题解算精度的相对均方误差分析方法

本发明涉及模型参数估计精度分析，尤其是涉及一种病态问题解算精度的相对均方误差分析方法。

背景技术：

1、卫星与传感器技术的发展为大地测量提供了更为丰富和高效的观测手段，然而由于观测条件以及观测环境的限制，在poinsar（polarimetric interferometric syntheticaperture radar）地表参数反演、gnss（global navigation satellite system）空间环境参数反演以及地球重力场反演等大地测量反演中常会出现病态问题，严重影响了物理参数反演的有效性与可靠性，须采用合理的病态问题解算方法，有效降低病态性对参数估计影响，提高物理参数的反演精度。

2、正则化方法与tsvd（truncated singular value decomposition）方法是目前最为常用的病态问题解算方法，可有效改善病态模型参数的反演精度与稳定性。其中，正则化方法在最小二乘估计的基础上增加稳定泛函约束，并引入正则化参数调节稳定泛函的约束作用，从而改善参数估计的稳定性。tsvd方法则利用奇异值分解技术对反演模型设计矩阵进行奇异值分解，利用截断参数将影响参数估值方差的较小奇异值截掉，进而实现参数估值精度的改善。针对不同实际应用场景，尽管正则化方法与tsvd方法均是可行且有效的病态问题解算方法，但两者解算方式的不同导致两种方法的解算精度与适用场景有所不同。实际应用中，应选择最为适合的解算方法以提高模型参数的反演质量。然而，由于病态性对参数估值方差的严重影响，通过常规精度分析方法难以确定出两种解算方法的优劣。文献“均方误差意义下正则化解优于最小二乘解的条件”指出在均方误差意义下，病态问题解算方法通过引入少量偏差，大幅降低方差，从而实现均方误差的下降。因此，通过分析均方误差的下降量可确定出更优的解算方法。然而，均方误差的计算需要模型参数真值，在实际应用中，参数真值是未知的，均方误差也难以准确计算。文献“利用均方误差相对变化规律确定正则化参数及其在polinsar测量反演中的应用”提出利用不同正则化参数下的正则化估值均方误差相对变化确定最优的正则化参数，来改善正则化法模型参数的估值精度。该算法有效避免了均方误差计算对真值的依赖，但针对不同形式的病态问题解算方法，无法实现参数估值精度的比较分析。鉴于此，本发明基于文献中均方误差相对变化思想，考虑利用不同解算方法的均方误差相对变化规律，提出一种病态问题解算精度的相对均方误差分析方法，实现不同病态问题解算方法的参数估值精度比较分析，进而确定出最优的解算方法。

技术实现思路

1、本发明的目的是提供一种病态问题解算精度的相对均方误差分析方法，通过计算均方误差相对变化，避免计算过程中参数真值的引入，实现病态问题解算方法的参数估值误差比较分析，进而确定出更优的解算方法，提高模型参数估值精度。

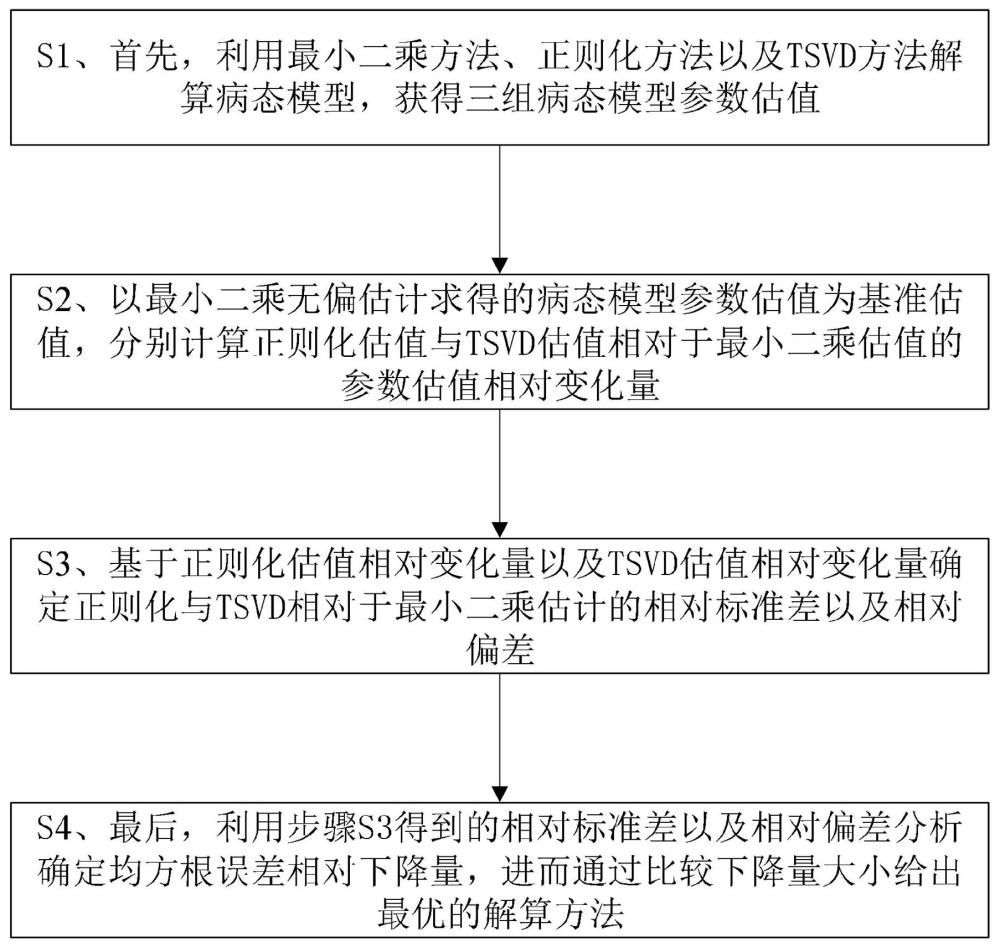
2、为实现上述目的，本发明提供了一种病态问题解算精度的相对均方误差分析方法，包括以下步骤：

3、s1、首先，利用最小二乘方法、正则化方法以及tsvd方法解算病态模型，获得三组病态模型参数估值；

4、s2、以最小二乘无偏估计求得的病态模型参数估值为基准估值，分别计算正则化估值与tsvd估值相对于最小二乘估值的参数估值相对变化量；

5、s3、基于正则化估值相对变化量以及tsvd估值相对变化量确定正则化与tsvd相对于最小二乘估计的相对标准差以及相对偏差；

6、s4、最后，利用步骤s3得到的相对标准差以及相对偏差分析确定均方根误差相对下降量，进而通过比较下降量大小给出最优的解算方法。

7、优选的，在步骤s1中，利用三种解算方法解算病态模型，获得病态模型参数的三组估值：

8、由最小二乘方法获得病态模型参数的最小二乘估值：

9、 (1)

10、式中，表示病态模型参数的最小二乘估值；为转置符号；表示模型设计矩阵；表示权重矩阵；为观测数据；

11、由正则化方法获得模型参数的正则化估值：

12、 (2)

13、式中，表示病态模型参数的正则化估值；为正则化参数，为单位矩阵；

14、由tsvd方法获得病态模型参数的正则化估值：

15、 (3)

16、式中，表示模型参数的tsvd估值；为设计矩阵的右奇异向量矩阵；为左奇异向量矩阵；为奇异值矩阵。

17、优选的，在步骤s2中，计算病态模型参数正则化估值以及tsvd估值相对于最小二乘估值的病态模型参数估值相对变化量：

18、 (4)

19、式中，表示正则化估值相对变化量；表示求模运算；

20、 (5)

21、式中，表示tsvd估值相对变化量。

22、优选的，在步骤s3中，无参数真值输入情况下，利用正则化估值与tsvd估值分别确定二者相对于最小二乘估值的相对标准差，包括：

23、最小二乘方法的方差计算式表示为：

24、 (6)

25、式中，为最小二乘方差；表示未知模型参数的个数；为单位权方差，由仪器标称精度或多余观测获得；为设计矩阵的奇异值；表示奇异值序号；

26、正则化方法的方差计算式表示为：

27、 (7)

28、式中，为正则化方差；tsvd方法的方差计算式则表示为：

29、 (8)

30、式中，为tsvd方差；

31、正则化法与tsvd法相对于最小二乘法的相对标准差计算为：

32、  (9)

33、 (10)

34、式中，表示正则化方法的相对标准差；表示tsvd相对标准差。

35、优选的，在步骤s3中，无参数真值输入情况下，利用正则化估值相对变化量与tsvd估值相对变化量分别确定正则化与tsvd相对于最小二乘方法的相对偏差，包括：

36、病态模型参数估值的均方误差表示为：

37、 (11)

38、式中，表示均方误差，表示数学期望运算，为病态问题解算方法模型参数估值，为模型参数真值，为病态问题解算方法估值方差，表示偏差；

39、由均方误差公式得病态问题解算方法相对于最小二乘方法的相对均方根误差为：

40、 (12)

41、式中，表示相对均方根误差，表示病态问题解算方法的估值均方根误差；表示最小二乘估计的均方根误差，因此，相对均方根误差近似为参数估值变化量之和，即：

42、 (13)

43、进而可得正则化方法与tsvd方法相对于最小二乘方法的相对均方根误差为：

44、 (14)

45、 (15)

46、式中，表示正则化方法的相对均方根误差；表示tsvd方法的相对均方根误差；

47、相对均方根误差由相对标准差和相对偏差两部分组成，因此，由相对均方根误差以及相对标准差得正则化与tsvd方法的相对偏差：

48、 (16)

49、 (17)

50、式中，为正则化方法参数估值相对偏差，为tsvd方法参数估值相对偏差。

51、优选的，在步骤s4中，绝对偏差无法有效计算时，利用正则化方法与tsvd方法相对于最小二乘方法的相对标准差和相对偏差，确定正则化方法与tsvd方法相对于最小二乘方法的均方根误差下降量，通过比较均方根误差相对下降量大小判断两种方法的解算效果：

52、 (18)

53、 (19)

54、式中，表示正则化方法均方根误差相对下降量；表示tsvd方法均方根误差相对下降量，均方根误差相对下降量越大则参数估计结果越优，由此得：

55、 (20)

56、基于上式即可判定出解算精度更优的解算方法。

57、因此，本发明采用上述一种病态问题解算精度的相对均方误差分析方法，基于正则化估值相对变化量以及tsvd估值相对变化量确定两方法相对于最小二乘估计的相对偏差，避免了偏差计算对参数真值的依赖。而后利用相对偏差以及相对标准差差值分析均方根误差相对下降量，进而通过比较下降量大小给出最优的解算方法。最后通过空间坐标测量实验以及polinsar植被高反演实验验证了精度相对分析方法的可行性与有效性。

58、下面通过附图和实施例，对本发明的技术方案做进一步的详细描述。