基于自适应支持向量机的机电伺服系统动态面滑模控制方法与流程

本发明涉及一种基于自适应支持向量机的机电伺服系统动态面滑模控制方法，特别是带有系统部分状态不可测、参数不确定以及外部扰动的机电伺服系统动态面滑模控制方法。

背景技术：

机电伺服系统是以电动机作为动力驱动元件的伺服系统，广泛应用于飞行控制、火力控制等各种领域。但是，系统中的不确定、不可测因素会大大影响伺服系统的控制精度，甚至严重降低机电伺服系统的性能，并且这些不确定因素的表现形式较为复杂，不易建模。因此，如何有效地控制和消除这些不确定因素影响，已成为机电控制中亟待解决的关键问题之一。

动态面控制方法(Dynamic Surface Control)在实现不确定非线性系统的鲁棒控制或自适应控制方面有着明显的优越性，受到国内外学者的极大关注。该方法利用系统的结构特性递推地构造整个系统的Lyapunov函数，使得控制器的设计结构化、系统化。针对反步控制法(Back-stepping Control)中可能导致微分项膨胀的问题，动态面控制方法在每一步设计中引入一阶积分滤波器，使得每一步设计的虚拟控制输入通过该滤波器，从而避免了系统中一些非线性函数的微分计算和控制器微分项的膨胀问题。

滑模控制(Sliding mode control)被认为是在解决系统不确定性和外部扰动的有效的鲁棒控制方法。滑模控制方法具有算法简单、响应速度快、对外界噪声干扰和参数摄动鲁棒性强等优点。因此，动态面控制方法与滑模控制方法的结合，可以使系统的控制器输入变得简单，系统的性能得到了提升。

支持向量机(SVM)最开始主要应用于模式识别领域，但是由于研究不完善，支持向量机一直没有得到重视。随着统计学习理论(Statistical Learning Theory，SLT)的发展，支持向量机成为机器学习领域的新研究热点。支持向量机基于统计学理论，具有严格的数学基础。结合统计学理论的VC维理论和结构风险最小化原理，使得机器学习的泛化能力大大增强，这也是支持向量机优于神经网络的最重要的地方。

技术实现要素：

为了克服现有技术的系统部分状态参数不确定的缺点，并消除不确定因素对机电伺服系统性能的影响，本发明提出一种基于自适应支持向量机的机电伺服系统动态面滑模控制方法，利用自适应支持向量机的函数逼近功能对系统中的不确定因素进行准确建模，并结合动态面控制和滑模控制方法设计自适应控制器。由于系统中的不确定因素已经得到了补偿，系统的跟踪性能得到了提高。

为了解决上述技术问题提出的技术方案为：

一种基于自适应支持向量机的机电伺服系统动态面滑模控制方法，包括如下步骤：

步骤1，建立如式(1)所示的机电伺服系统模型，初始化系统状态以及控制参数；

其中，θ_m，ω_m为状态变量，分别表示电机输出轴位置和转速；J和D是折算到电机轴上的等效转动惯量和等效阻尼系数；K_t是电机扭矩常数；u是控制量；T_l是折算到电机轴上的负载扭矩；T_N是折算到电机轴上的摩擦力；

步骤2，对系统模型进行简化变形，过程如下：

其中，y＝x₁＝θ_m，x₂＝ω_m；

步骤3，用动态面滑模的方法来设计控制器u，过程如下：

3.1，定义跟踪误差，滑模面为：

其中，e₁为跟踪误差，y_d为跟踪参考信号，y为电机输出轴位置，s₁为定义的滑模面；

对s₁求导得：

其中，是带有不确定项的函数；

3.2，用自适应支持向量机的方法对进行建模：

令

其中，和分别是核函数h₁的理想权重，支持向量和宽度；ε_a1是固有在线逼近误差；

3.3，选择虚拟控制器

用z₂做的一阶滤波器可得：

定义：

其中，k₁是正常数，和分别是和的估计；设计这些估计值的迭代公式：

其中γ₁,κ₁,γ_sv,1,κ_sv,1,γ_σ,1和κ_σ,1是正常数；

3.4，定义控制器控制误差s₂：

s₂＝x₂-z₂ (10)

令

其中

其中和分别是核函数h₂的理想权重，支持向量和宽度,是固有在线逼近误差；

3.5，设计控制器：

其中，k₂是正常数，和分别是和的估计；设计这些估计值的迭代公式：

其中γ₂,κ₂,γ_sv,2,κ_sv,2,γ_σ,2和κ_σ,2是正常数；

3.6，设计李雅普诺夫函数：

对(15)求导得

利用不等式ab≤|a||b|≤a²+b²/4得

其中B_i+1，μ，η，Γ₂，为有限值的正常数；

由此可得，最终一致有界，判定系统稳定。

本发明结合自适应支持向量机和动态面滑模控制技术，设计基于自适应支持向量机的动态面滑模控制器，实现机电伺服系统的位置准确跟踪控制。

本发明的技术构思为：机电伺服系统中由于存在各种不确定因素而导致控制精度不高。针对部分状态不可测、参数不确定以及存在外部扰动的机电伺服系统，运用自适应支持向量机，结合动态面滑模控制理论，设计一种基于自适应支持向量机的机电伺服系统动态面滑模控制方法，尽可能地消除了不确定因素对系统控制的影响。通过自适应支持向量机建模，设计动态面滑模控制器保证系统跟踪误差快速稳定地收敛至零点，实现机电伺服系统的快速稳定控制。

本发明的优点为：能准确建模，提高系统的跟踪精度和鲁棒性，改善系统的跟踪性能。

附图说明

图1为本发明的自适应支持向量机建模曲线的示意图；

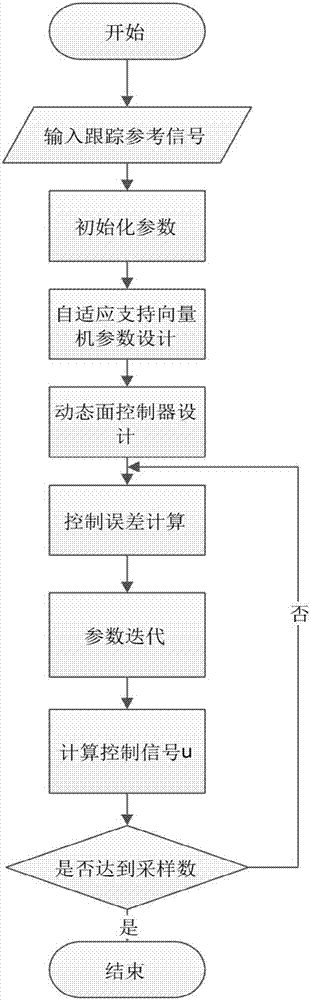
图2为本发明的算法的基本流程图；

图3为本发明的控制系统响应曲线的示意图；

图4为本发明的控制系统跟踪误差的示意图；

图5为本发明的控制信号输出的示意图。

具体实施方式

下面结合附图对本发明做进一步说明。

参照图1-图5，一种基于自适应支持向量机的机电伺服系统动态面滑模控制方法，包括如下步骤：

步骤1，建立如式(1)所示的机电伺服系统模型，初始化系统状态以及控制参数；

其中，θ_m，ω_m为状态变量，分别表示电机输出轴位置和转速；J和D是折算到电机轴上的等效转动惯量和等效阻尼系数；K_t是电机扭矩常数；u是控制量；T_l是折算到电机轴上的负载扭矩；T_N是折算到电机轴上的摩擦力；

步骤2，对系统模型进行简化变形，过程如下：

其中，y＝x₁＝θ_m，x₂＝ω_m；

步骤3，用动态面滑模的方法来设计控制器u，过程如下：

3.1，定义跟踪误差，滑模面为：

其中，e₁为跟踪误差，y_d为跟踪参考信号，y为电机输出轴位置，s₁为定义的滑模面；

对s₁求导得：

其中，是包含不确定项的函数；

3.2，用自适应支持向量机的方法对进行建模：

令

其中，和分别是核函数h₁的理想权重，支持向量，和宽度；ε_a1是固有在线逼近误差；

3.3，选择虚拟控制器

用z₂做的一阶滤波器可得：

定义：

其中，k₁是正常数，和分别是和的估计；设计这些估计值的迭代公式：

其中γ₁,κ₁,γ_sv,1,κ_sv,1,γ_σ,1和κ_σ,1是正常数；

3.4，定义控制器控制误差s₂：

s₂＝x₂-z₂ (10)

令

其中

其中和分别是核函数h₂的理想权重，支持向量和宽度,是固有在线逼近误差；

3.5，设计控制器：

其中，k₂是正常数，和分别是和的估计；设计这些估计值的迭代公式：

其中γ₂,κ₂,γ_sv,2,κ_sv,2,γ_σ,2和κ_σ,2是正常数；

3.6，设计李雅普诺夫函数：

对(15)求导得

利用不等式ab≤|a||b|≤a²+b²/4得

其中B_i+1，μ，η，Γ₂，为有限值的正常数；

由此得，最终一致有界，判定系统稳定。

为验证所提方法的有效性，本发明对由式(13)表示的动态面滑模控制器的控制效果进行仿真实验，设置仿真实验中的初始条件与部分参数，即：系统方程中J＝0.5，K_t＝1，D＝0.3，T_l＝0.5。式(6)，(13)中的参数为k₁＝10，k₂＝10。自适应支持向量的参数为r₁＝r₂＝5，r_sv,1＝r_sv,2＝0.5，r_σ,1＝r_σ,2＝0.3，κ₁＝κ₂＝0.05，κ_sv,1＝κ_sv,2＝0.05，κ_σ,1＝κ_σ,2＝0.02。

从图3可以看出，本发明设计的基于自适应支持向量机动态面滑模控制方法可以实现实际系统输出对期望轨迹y_d＝0.5(sin(t)+sin(0.5t))的快速有效跟踪。从图4可以看出，跟踪误差在1.5s后便趋于稳定范围[-0.2,0.2]，说明该方法能有效提高跟踪精度，降低跟踪误差。从图5可以看出，控制信号收敛。整体来看，基于自适应支持向量机的机电伺服系统动态面滑模控制方法可以改善系统的跟踪性能。

以上阐述的是本发明给出的一个实施例表现出的优良优化效果，显然本发明不只是限于上述实施例，在不偏离本发明基本精神及不超出本发明实质内容所涉及范围的前提下对其可作种种变形加以实施。所提出的控制方案对存在模型不确定项的机电伺服系统是有效的，在所提出的控制器的作用下，实际输出能很快跟踪上期望轨迹。