一种基于改进正交优化群智能算法的分布式电源规划方法与流程

本发明一种基于改进正交优化群智能算法的分布式电源规划方法，涉及微电网规划领域。

背景技术：

随着全球经济的加速发展，能源短缺、环境污染成为当今社会面临的巨大挑战。由于电力负荷持续增长、电力系统结构老化、能源利用效率瓶颈、用户对高标准电能质量的要求以及环保等问题，迫切需要发展清洁、无污染的可再生能源发电方式，作为传统集中式发电的有效补充，分布式发电技术应运而生。分布式发电是指将发电系统以小规模(发电功率在数千瓦至50MW的小型模块分散式的方式布置在用户附近,可独立地输出电能的系统。分布式发电设施主要包括以液体或气体为燃料的内燃机、微型燃气轮机、风力发电、光伏电池等。然而分布式电源的不合理规划，不仅会导致资金的浪费，还会造成配电网电压质量，有功网损等配电网技术指标的恶化。因此，对分布式电源进行科学的规划，对于配电网的经济发展、安全运行有着积极作用。

分布式电源的规划一般包括确定位置和容量两部分。国内外学者对分布式电源的规划进行了大量的研究，优化算法主要有启发式优化算法和数学优化算法。学者们提出了很多改进启发式智能算法，通过设计正交试验来实现最优解区间的搜索，例如正交遗传算法、正交交叉算子的元胞差分进化算法、正交免疫克隆粒子群算法等，但是这些算法仅仅在种群初始化过程设计正交试验，并没有完全利用正交设计的搜索功能。

技术实现要素：

为解决上述技术问题，本发明综合考虑分布式电源规划经济性和安全可靠性，建立以DG投资和运行成本、有功网损、电压偏移量为目标函数的多目标优化模型，提出一种改进正交优化群智能算法对分布式电源的选址和定容进行优化求解，并将其优化结果与遗传算法的优化结果相比较，验证该算法的可行性和优异性。

一种基于改进正交优化群智能算法的分布式电源规划方法，包括以下步骤：

1)、以系统有功网损、投资运行成本及负荷点电压偏移量为优化指标建立多目标优化模型。

2)、初始化，输入节点网络的原始数据；

3)、构建初始正交表L_a(b^c)，计算正交表的局部最优值；

4)、进行方差比例分析：在正交表的方差分析中，计算出各变量的方差比例ρ_i，根据方差比例建立新的正交表，反复进行迭代优化，直到找到最优解。

本发明一种基于改进正交优化群智能算法的分布式电源规划方法，有益效果如下：

1)本发明的提出以配电网有功功率损耗、电压偏移量、投资和运行成本为优化目标，较为全面考虑了分布式电源的规划。

2)、本发明的提出对于分布式电源规划中减少有功功率损耗、降低系统电压偏移量有明显作用。

3)、突破了正交设计仅能用于种群初始化和进化前优化搜索的限制。

4)、通过方差比例分析提供进一步正交优化的搜索方向和搜索范围，拟降低优化搜索计算量和搜索时间，提高微电网配置优化算法效率和可用性。

5)、提出了一种新的改进正交优化群智能算法的分布式电源规划，为今后分布式电源规划提供了新的思路。

附图说明

图1是实施例中IEEE14节点配电系统配电网络结构图。

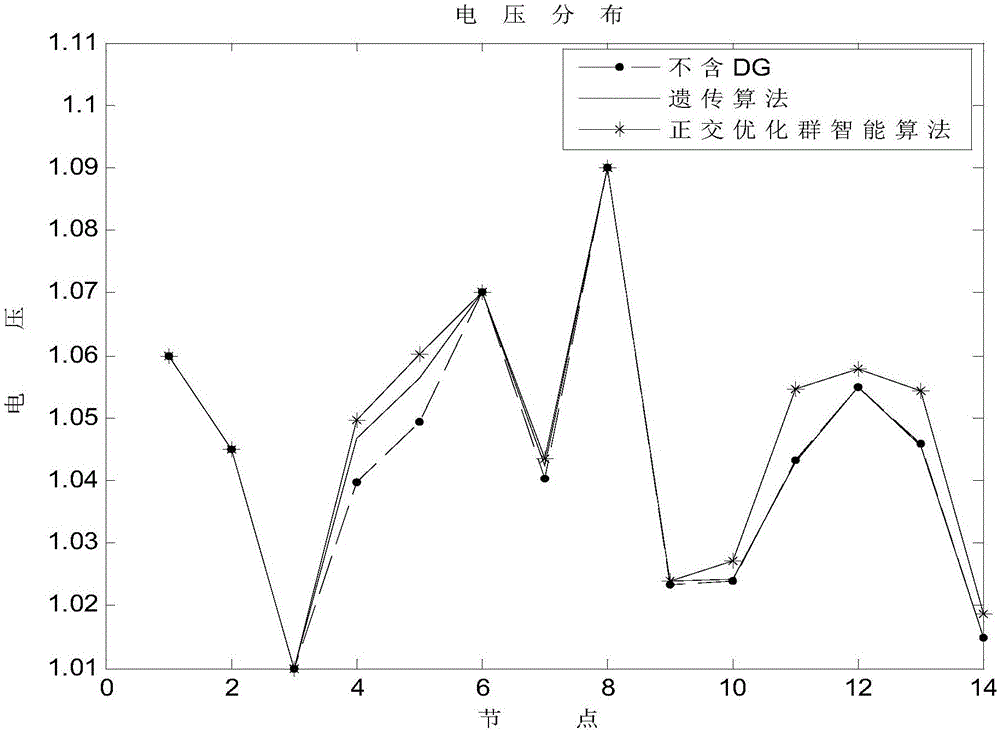
图2是实施例中不含DG规划、基于遗传算法DG规划、基于改进正交优化群智能算法的DG规划三种情况下的电压分布图。

具体实施方式

一种基于改进正交优化群智能算法的分布式电源规划方法，包括以下步骤：

1)、以系统有功网损、投资运行成本及负荷点电压偏移量为优化指标建立多目标优化模型。

2)、初始化，输入节点网络的原始数据；

3)、构建初始正交表L_a(b^c)，计算正交表的局部最优值；

4)、方差比例分析。在正交表的方差分析中，计算出各变量的方差比例ρ_i，根据方差比例建立新的正交表，反复进行迭代优化，直到找到最优解。

本发明一种基于改进正交优化群智能算法的分布式电源规划方法，将分布式电源规划应用于正交试验中，并且在正交试验的DG容量方差分析中加入方差比例分析，为DG的规划提供搜索方向和搜索范围，寻求最优解。最后通过实际算例仿真计算，并与遗传算法相比较，验证了该算法的有效性和优异性，为分布式电源的规划提供了新的思路。

具体步骤如下：

步骤1)：建立分布式电源规划优化模型。分布式电源规划中，要求具有较优的配电网的有功网损、投资运行成本及负荷点电压偏移量等。其中，配电网的有功网损f₁最小如下，

式中，P_loss为配电网有功网损；G_k(i,j)相应支路k的电导；U_i，U_j分别为节点i,j的电压幅值；δ_ij为相应节点i，j的电压相角差。

分布式电源投资运行成本f₂最小如下

式中，N_DG为安装DG的节点数，C_az,i为i节点运行维护成本，C_OM,i为i节点安装投资成本单位为万元/(KW·h)；P_DGi为i节点DG容量；n为DG的使用年限；r为贴现率；

负荷点电压偏移量f₃最小如下：

式中，U_i，分别表示负荷节点i的实际电压、期望电压和最大允许电压偏差,

以配电网的有功功损、分布式电源投资运行成本、负荷点电压偏移量为评价目标，分布式电源选址和定容的多目标优化模型如式子所示：

min f＝(f₁,f₂,f₃) (4)

步骤2)：给分布式电源规划模型建立约束条件，其中约束条件分为不等式约束条件与等式约束条件，不等式约束条件：

DG总有功功率约束条件

式中，P_DG.i为节点i的DG安装容量，P_DG..all为DG总有功功率上限。

DG的节点电压约束条件：

V_imin≤V_i≤V_imax,i＝1,2,…,N_B (6)

式中，V_imin，V_imax分别为节点i的电压下限与上限；N_B为系统节点总数。

DG的有功功率约束条件：

0≤P_DGi≤P_DGimax,i＝1,2,…,N_DG (7)

式中，P_DG.imax为节点i的DG上限；

DG等式约束条件为:

式中，G_ij，B_ij分别为节点i，j间的电导和电纳；P_Gi，Q_Gi分别为节点i发电机的有功功率和无功功率；P_Li，Q_Li分别为节点i负荷的有功功率和无功功率；

步骤3)：初始化系统网络的参数：节点网络的支路数据电导G_ij和电纳B_ij；负荷端有功功率P_Li以及无功功率Q_Li；系统的发电机有功功率P_Gi以及无功功率Q_Gi；确定电压上下限V_imin、V_imax；各节点分布式电源的容量P_DGi

步骤4)：正交试验设计是用部分试验来代替全面试验，通过对部分试验结果的分析，了解全面试验的情况。根据任露泉.《试验优化设计与分析(第二版)》，高等教育出版社，2008，正交试验方案的主要步骤为：

(1)明确试验目的，确定试验指标。

(2)确定需要考察的因素，选取适当的水平。

(3)选用合适正交表。

(4)进行表头设计。

(5)编制试验方案。

根据模型的需求确定代表分布式电源规划正交试验的样本数a、代表分布式电源容量的正交表因素水平数b、代表节点数的正交表列数c，确实正交表各因素各水平代表数值，构建正交表L_a(b^c)。例如：本发明对IEEE14节点系统进行DG规划，节点1为平衡节点，不安装DG，其余13个节点都设计三种水平的DG安装容量：节点2为B₁、B₂、B₃，节点3为C₁、C₂、C₃，节点4为D₁、D₂、D₃，…，设计的正交表L₂₇(3¹³)如表1所示。

表1 IEEE14节点系统正交表L₂₇(3¹³)

步骤5)：并根据所建立的多目标函数和约束条件，对配电网系统进行潮流计算，对正交表各个试验号进行潮流计算，得到分布式电源规划相应的配电网的有功网损、投资运行成本及负荷点电压偏移量的试验结果。

步骤6)：建立模糊综合评判矩阵，找出局部最优值。设c_ij(i＝1，2，3；j＝1，2，3,…，a)表示第个i优化目标(有功网损，投资运行成本，电压偏移量)的第j个试验结果。

式中，r_ij表示第个i优化目标(有功网损，投资运行成本，电压偏移量)中第j个试验结果的值在相应优化目标值总和中所占的比例。

由式子(9)得到模糊综合评判矩阵R＝(r_ij)_3×a。根据经验设置三个优化目标的权系数向量A＝(a₁，a₂，a₃)，通过加权平均法计算综合评判向量B_1×a，综合评判向量中最小值所对应的试验号即为分布式电源规划的局部最优值X＝(x₁，_x2，x₃,…,x_c,)。

b_j＝∑(a_i·r_ij)(j＝1,2…a) (10)

式中，a_i为权系数值，b_j为综合评判值。

步骤7)：对正交表进行方差分析，计算网络系统各位置DG容量的方差比例：

式中，SS_j指因素j的偏差平方和，y_i为每个试验号的综合评判值，KK_ij指正交表第j列因素的第i个水平的综合评判值的总和，k指相应因素的水平数。

式中，SS_T指总偏差平方和。

由统计概论学：

式中，SS_A是因素A的偏差平方和，SS_A包含指数A的纯粹波动平方和以及部分误差的波动平方，σ²为正交试验的方差，k为因素A的水平数；

σ²的无偏估计量如下式：

式中，为σ²的无偏估计量，E为求期望；

指数A引起的纯粹波动平方和:

SS_A'＝SS_A-(k-1)V_e (15)

式中，SS’_A为A的纯粹波动平方和；

计算误差引起的纯粹波动平方和:

SS_e'＝SS_e+(k-1)V_e (16)

式中，SS_e为误差偏差平方和，SS’_e为误差的纯粹波动平方和；

方差比例定义为纯粹波动平方与占总波动比:

ρ_A+ρ_B+…+ρ_M+ρ_e＝1

式中，SS_T为总偏差平方和，ρ_i为各因素i的方差比例，ρ_e为误差的方差比例；

将传统方差分析方法和纯粹波动相结合，得到基于纯粹波动的方差比例分析方法，根据式(11)—式(17)计算出各变量的方差比例ρ_i。

步骤8)：构造新的正交表。根据上一轮迭代得到的分布式电源容量的局部最优解X＝(x₁，x₂，x₃,…,x_c,)以及各因素的方差比例ρ_i，根据式子(18)更新各个节点的三种DG容量水平的值(本发明设计为三水平正交表)，将各节点新的DG容量水平值按表1的顺序构造一个新的正交表。

步骤9)：反复迭代步骤5)～步骤8)，直到各节点方差比例相等时，迭代结束，进入步骤10)。

步骤10)：改进正交优化群智能算法结束，最后一次迭代得到的最优解即为DG规划的最优解X^*＝(x^*₁，x^*₂，x^*₃,…,x^*_c)。

实施例：

以IEEE14节点网络系统为例：

根据本发明提出的分布式电源规划数学模型以及改进正交优化群智能算法，通过MATLAB对IEEE14节点配电系统进行仿真，其配电网络结构如图1所示，标幺值为100MVA，各节点的电压0.97～1.1倍基准电压，系统总负荷为259.9MW+73.5Mvar。将分布式电源作为普通的PQ点来处理，设节点1为平衡节点。在多目标模型的模糊综合评估，有功网损、电压偏移量、投资和运行成本的权重分别为1/2，3/8，1/8，分布式电源的规划如表2所示。

表2 分布式电源安装位置和安装容量

从表2可以看出，根据遗传算法进行分布式电源规划：2，4，6三个节点，安装容量分别为：0.25MW，0.25MW，0.25MW；根据改进正交优化群智能算法进行分布式电源规划：4，6，11，13四个节点，安装容量分别为：0.118MW，0.193MW，0.25MW，0.1889MW。

表3为分布式电源规划优化结果与优化前的比较：

表3 优化前和优化后结果

图2为不含DG规划，基于遗传算法DG规划和基于改进正交优化群智能算法的DG规划三种情况下的电压分布图。

表3可以看出，不含DG的配电网的有功网损为0.2765MW，电压偏移量为0.2394。两种含有DG规划配电网的有功网损和电压偏移量均比不含DG配电网的小；由图2可看出DG规划的电压稳定性要比不含DG规划要略好，所以DG规划效果明显。

为了进一步验证改进正交优化群智能算法的有效性以及优越性，在数学模型与约束条件相等条件下，将其与遗传算法相比较，由表2得遗传算法的有功网损为0.1717MW，电压偏移量为0.236，DG投资与运行成本为599.1326万元；改进正交优化群智能算法的有功网损为0.1599MW，电压偏移量为0.2296，DG投资与运行成本为599.0527万元。通过对比，算法在三个方面均优于遗传算法，并且图2中改进正交优化群智能算法电压稳定较好，因此改进正交优化群智能算法优化效果更好。