一种低频预紧式双稳态振动能量收集器及制作方法

本发明涉及振动能量收集技术领域，尤其涉及一种低频预紧式双稳态振动能量收集器及制作方法。

背景技术：

目前对于海浪能的能量回收主要是依靠电磁式发电机，通过电磁感应定律来将机械能转换成电能。但同时也发现了电磁发电的缺陷，它只能针对高频振动激励来进行能量转换，而近年来对压力发电和摩擦发电的开发都有了新的发现和应用，它们以其能够针对低频能量和更高的发电效率凸显出自身的优势，但同时难以大面积进行能量回收以及对结构设计要求高的特点，也使得对它们的开发受到了限制。

技术实现要素：

基于背景技术存在的技术问题，本发明提出了一种低频预紧式双稳态振动能量收集器及制作方法，通过悬臂梁自身发生形变而产生内在的弹力势能来作为双势阱的压力源，提高了在低频振动环境下的工作效率。

本发明提出的一种低频预紧式双稳态振动能量收集器，包括能量回收装置、一端固定的立杆和具有一定弯曲挠度的悬臂梁，悬臂梁的一端与能量回收装置固定连接、另一端与立杆自由端固定连接。

进一步地，所述悬臂梁与能量回收装置的连接处设置有树脂板，螺钉依次穿过悬臂梁、树脂板、能量回收装置的凸台端固定。

进一步地，所述立杆和悬臂梁数量对应设置，每个悬臂梁的一端能量回收装置固定连接、另一端与对应的立杆自由端固定连接。

进一步地，6个悬臂梁均匀分布于能量回收装置的外周。

进一步地，所述能量回收装置包括空心壳体和设置于空心壳体中的摩擦纳米发电机，空心壳体采用树脂材质。

所述悬臂梁弯曲挠度的总机械能u(z)公式如下：

a＝w(2tp+ηstsh)

ηs＝ec/ep

其中，ub表示弯曲势能，uc表示压力势能，ep为悬臂梁的杨氏模量，i表示悬臂梁横截面的惯性矩，z表示在对悬臂梁总长度l0施加横向位移为δl静力载荷时，悬臂梁中心的弯曲位移，l表示弯曲悬臂梁首尾连接的直线长度，l＝l0-δl，a为悬臂梁的等效横截面积，z0为δl不变时，悬臂梁中心点的最大弯曲位移，e表示悬臂梁的杨氏等效模量，是悬臂梁的第一模态函数，w表示悬臂梁的宽度，tsh表示悬臂梁的厚度，tp表示能量回收装置的厚度，ec为弹性元件的杨氏模量。

一种低频预紧式双稳态振动能量收集器，能量回收装置、立杆和悬臂梁，悬臂梁的两端分别与能量回收装置和立杆固定连接；

其中悬臂梁的弯曲挠度设置方法如下：

构建预紧式双稳态结构，得到外部激励力f与悬臂梁本体参数对应的势能函数，所述悬臂梁本体参数包括悬臂梁中间质量块的重量、悬臂梁中间部分的加速度、悬臂梁中间部分的速度以及悬臂梁中间部分的弯曲位移；

基于所述能量回收装置中摩擦纳米发电机的重量和形状体积，构建以所述悬臂梁作为弹性结构的双稳态运动模型；

改变所述悬臂梁长度和横截面积，输入所述双稳态运动模型，输出跨越双稳态壁垒的双稳态势能函数，实现能量回收装置更宽的工作频域和振幅。

一种计算机可读储存介质，其特征在于，所述计算机可读存储介质上存储有若干获取分类程序，所述若干获取分类程序用于被处理器调用并执行如上所述的低频预紧式双稳态振动能量收集器。

本发明提供的一种低频预紧式双稳态振动能量收集器及制作方法的优点在于：本发明结构中提供的一种低频预紧式双稳态振动能量收集器及制作方法，依靠外部激励产生的惯性力带动悬臂梁上下摆动来跨越双稳态的壁垒进行拓频能量回收，因而通过悬臂梁自身发生形变而产生内在的弹力势能来作为双势阱的压力源，提高了在低频振动环境下的工作效率。

附图说明

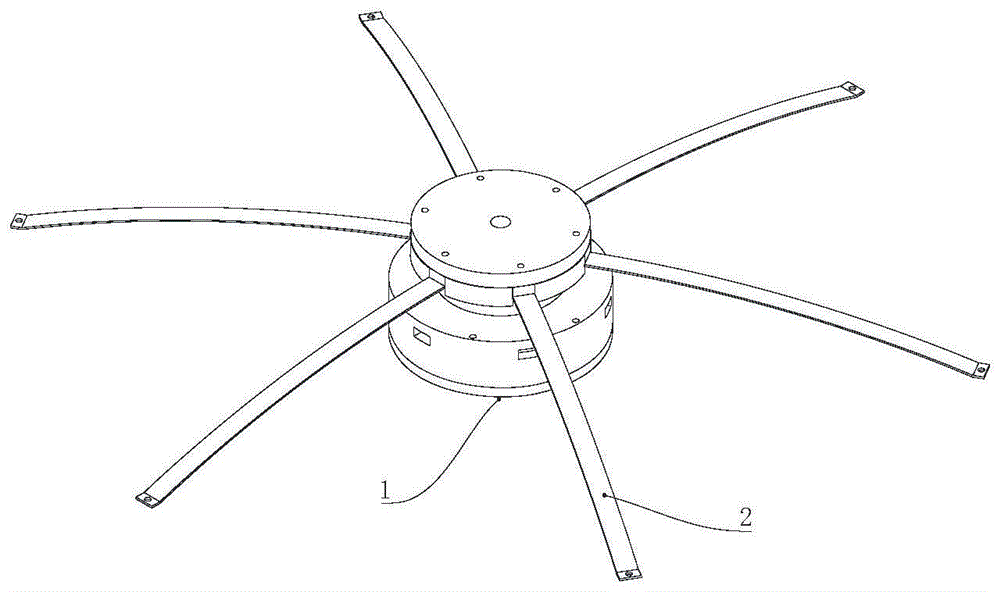
图1为本发明的结构示意图；

图2为预紧式双稳态结构模型示意图；

图3为非线性势能函数u(x)的曲线图；

图4为改变初始位移z0和悬臂梁横截面积a的情况下，得到的不同弯曲位移z下的势能函数u(z)；

图5为没有双稳态结构(悬臂梁)的情况下，摩擦纳米发电机产生的电压图；

图6为添加双稳态结构(悬臂梁)的情况下，摩擦纳米发电机产生的电压图；

图7为摩擦纳米发电机在加入双稳态后，在外部激励10mm的振幅下，不同频率的振幅图

其中，1-能量回收装置，2-悬臂梁。

具体实施方式

下面，通过具体实施例对本发明的技术方案进行详细说明，在下面的描述中阐述了很多具体细节以便于充分理解本发明。但是本发明能够以很多不同于在此描述的其他方式来实施，本领域技术人员可以在不违背本发明内涵的情况下做类似改进，因此本发明不受下面公开的具体实施的限制。

目前波浪能主流应用的情况包括以下几种：振荡水柱式波浪能收集器、振荡式波浪能收集器、收缩波道式波浪能收集器。都是依靠针对高频波浪能设计的电磁式发电机作为能量回收单元的能量回收装置们对于低频波浪能应用有限。

双稳态结构通过设计两个机械势阱，通过外部磁力或者内部弯曲应力来使整体结构能由最初的单稳态运动，变成在两个稳态之间来回跳动的双稳态运动，使得受迫进行振动的能量回收装置1在两个势阱之间来回振荡，从而提高能量回收装置的位移大小和能量输出功率。目前实现双稳态来达到拓拓宽频率范围的方法主包括两种：一种是依靠永磁体的排斥力和吸引来作为势阱的压力源，另一种则是通过压缩弹簧钢，使其自身发生形变而产生内在的弹力势能来作为双势阱的压力源。本申请通过设置具有一定挠度的悬臂梁2作为被压缩的弹簧钢，来实现拓频目的。

如图1所示为实现拓频的装置，本发明提出的一种低频预紧式双稳态振动能量收集器，包括能量回收装置1、一端固定的立杆和具有一定弯曲挠度的悬臂梁2，悬臂梁2的一端与能量回收装置1固定连接、另一端与立杆自由端固定连接。

悬臂梁2的设置数量可以根据需要进行设置，以下以6个悬臂梁2进行说明：同步设置6个立杆，立杆的作用是使得悬臂梁2具有一定的弯曲挠度，6个悬臂梁等角度分布于能量回收装置1的周边，使得整个能量收集器处于结构平衡状态。于悬臂梁2的固定，所述悬臂梁2与能量回收装置1的连接处设置有树脂板，以避免悬臂梁2振动，引起能量回收装置1的同步振动，从而造成能量回收装置1中结构、元器件等出现结构变形、脱落等缺陷，螺钉依次穿过悬臂梁2、树脂板、能量回收装置1的凸台端固定；悬臂梁2与立杆直接也可以通过螺钉穿过悬臂梁2端部，将悬臂梁2固定于立杆的自由端；悬臂梁2两端固定，中间位置发生一定的弯曲，实现悬臂梁2具有一定弯曲挠度的固定设置。

针对能量回收装置1，包括空心壳体和设置于空心壳体中的摩擦纳米发电机，空心壳体采用树脂材质，空心壳体11的柔性设置，结合波浪能的柔性流动，使得整个振动能量收集器更灵敏，进而提高了整个能量收集器的收集效率和质量。需要说明的是，摩擦纳米发电机可以采用现有的发电组件，即摩擦纳米发电机可以内部使用kapton薄膜和液态金属，通过液体流动形成电势差，进行摩擦发电，在此不做累述。

在本实施例中，对于悬臂梁2的弯曲挠度设置，需要遵循一定的设计要求，悬臂梁2的弯曲挠度设置方法如下：

s1：构建预紧式双稳态结构，得到外部激励力f与悬臂梁2本体参数对应的势能函数，所述悬臂梁2本体参数包括悬臂梁2中间质量块的重量、悬臂梁2中间部分的加速度、悬臂梁2中间部分的速度以及悬臂梁2中间部分的弯曲位移；

中间质量块的设置可以提高中间部分悬臂梁受到外界激励产生的惯性力。为了实现结构上产生的预紧式双稳态，如图2所示，首先要保证q＝x/2t>2.31，其中x为两个稳态之间的距离，即x为弯曲梁在上稳态弯曲位置与下稳态弯曲位置之间的距离，t为悬臂梁的厚度，悬臂梁2未压缩时的原始长度为l1，悬臂梁2压缩弯曲后首尾连接的直线长度l2，压缩距离y＝l2-l1。

在这个过程中上下稳态之间的距离x随压缩距离y的增加而增加。因此为了实现双稳态之间的相互转化，需要借助外部激励来越过双稳态之间的势垒，外部激励力的大小为f。所以需要确定压缩距离y，上下稳态之间距离x以及外部激励力f大小之间的关系。为此可以借助经典的二阶质量-阻尼-弹簧系统来对双稳态系统进行分析。由于双稳态系统，所以需要加入一个非线性项，其力学表达式为：

其中，m为悬臂梁中间质量块的重量，d为阻尼系数，表示悬臂梁中间部分的加速度，表示悬臂梁中间部分的速度，x表示悬臂梁中间部分偏离原始位置的弯曲位移，ψ(x)为恢复力。

恢复力ψ(x)是通过势能函数u(x)中对x求导而得：

非线性势能函数u(x)可以通过以下表达式来表达：

将式(3)带入式(1)可得式(4)：

根据式(4)可得到非线性势能函数u(x)的曲线图，如图3所示，由曲线图可以得出f(t)和x之间的对应关系，即可得出悬臂梁作为被压缩的弹簧钢，来实现拓频时，对应的较佳弯曲距离，进而对悬臂梁弯曲距离进行了优化设计。

s2：基于所述能量回收装置1中摩擦纳米发电机的重量和形状体积，构建以所述悬臂梁2作为弹性结构的双稳态运动模型；

采用如图2所示的双稳态构建方法，能够避免两端预紧梁在挠度函数存在二阶导数为零的振型节点。为了确定之后需要固定两端长度，可以利用这种模型来进行计算，同时它也能够更加方便地研究能量收集装置1在不同轴向压缩位移、激励加速度和振动频率下的输出特性。为了更好地计算势能函数，首先需要确定悬臂梁2的总长度l0，弯曲后悬臂梁2首尾连接的直线长度l，悬臂梁2的弯曲横向长度δl，从而可得以下关系：

l0＝l+δl

弯曲悬臂梁的总机械能u(z)由弯曲势能和ub和压缩势能uc构成，对应的公式如下：

a＝w(2tp+ηstsh)(8)

ηs＝ec/ep(10)

其中，ub表示弯曲势能，uc表示压力势能，ep为悬臂梁的杨氏模量，i表示悬臂梁横截面的惯性矩，z表示在对悬臂梁总长度l0施加横向位移为δl静力载荷时，悬臂梁中心的弯曲位移，l表示弯曲悬臂梁首尾连接的直线长度，l＝l0-δl，a为悬臂梁的等效横截面积，z0为δl不变时，悬臂梁中心点的最大弯曲位移，e表示悬臂梁的杨氏等效模量，是悬臂梁的第一模态函数，w表示悬臂梁的宽度，tsh表示悬臂梁的厚度，tp表示能量回收装置的厚度，tp取1，ec为弹性元件的杨氏模量，ec，ηs取1。

由于双稳态结构的存在，悬臂梁上不同的点x发生了竖直方向z的位移，通过第一模态函数，将这个位移和点的位置的关系转换成势能大小。

根据式(5)，在改变悬臂梁2长度从而改变初始位移z0(mm)和悬臂梁横截面积a(mm²)的情况下得到的不同弯曲位移z下的势能函数，如图4所示，从图中可以看出，悬臂梁2的长度和横截面积a对双稳态势能函数有着显著影响。悬臂梁2的长度越长，导致z0越大，从而使得两稳态之间间距相差过大，导致壁垒也随之增大；除此之外悬臂梁2的横截面积的增加会提高双稳态转换所需要的外部激励，所以壁垒也会增加。相反过小的壁垒则会降低双稳态结构托宽频域的效果，因而如图4中a＝30，z0＝20对应线条11的势能函数，就优于其他线条，所以相关参数也是使能量回收装置拥有最佳输出功率的结构参数。

s3：改变所述悬臂梁2长度和横截面积，输入所述双稳态运动模型，输出跨越双稳态壁垒的双稳态势能函数，实现能量回收装置1更宽的工作频域和振幅。

本申请的能量收集器主要依靠外部激励产生的惯性力带动悬臂梁上下摆动来跨越双稳态的壁垒进行拓频能量回收。这种能量回收模式称之为惯性力能量回收，它的主要工作频域主要集中在双稳态的两个势阱的谐振频域之间。谐振频率是指使弹性结构能够产生最大振幅的外部激励频率。双稳态系统受不同频率外部激励的影响是：

1.当外界激励的频率和双稳态结构的谐振频率相近时，双稳态系统的振幅一般为最大值，这个时候弹性结构的工作效率往往最高，适合用于能量回收。

2.当外部激励小于悬臂梁的的谐振频率时，双稳态结构只做小振幅的单稳态摆动，这时候的振幅受双稳态结构影响比外部激励振源的振幅要小。

3.当外部激励远大于悬臂梁谐振频率时，双稳态结构失效，悬臂梁将不会上下摆动，随着外部激励一同振动，振幅和振动频率和外部激励一致。

因此在拓宽双稳态势阱(拓宽能量回收装置工作频域)的前提下，保证双稳态势垒能在外部激励的振幅作用产生的惯性力能够被打破。通过这样的选择方式，可以使得能量回收装置1拥有更宽的工作频域和振幅大小，从而提高其输出功率。如图4中a＝30，z0＝20对应线条11的势能函数，就优于其他线条，所以相关参数也是使能量回收装置拥有最佳输出功率的结构参数。

在本实施例中，通过步骤s1至s3，悬臂梁的选择首先要满足步骤s1中的预紧式双稳态结构，以得到悬臂梁2的外部激励力与弯曲位移之间的关系，以保证当前悬臂梁2可以实现双稳态结构，然后悬臂梁还要满足步骤s2中悬臂梁2作为弹性结构的双稳态运动模型，从而在较大程度上获取低频波浪能下总机械能与悬臂梁的长度、横截面积之间的关系，然后通过步骤s3改变悬臂梁2长度和横截面积，根据不同长度和悬臂梁横截面积得到不同弯曲位移z下的势能函数，根据势能函数曲线图，得到较优的势能函数，因而对应得出具有一定长度、横截面积的悬臂梁2，进而将该悬臂梁2与能量回收装置1进行安装，即可得到低频预紧式双稳态振动能量收集器。

例如：

在没有双稳态结构(悬臂梁)的情况下，利用振动台产生10mm振幅，15hz频率的振动对液态摩擦纳米发电机激励，产生的电压图如图5所示，加入了双稳态(悬臂梁)后，摩擦纳米发电机的发电电压图如图6所示，通过图6可知，在加入双稳态后，摩擦纳米发电机在低频低振幅的外部激励下，从开始的接近50v的输出电压，增长到了接近125v的输出电压。

摩擦纳米发电机在加入双稳态后，在外部激励10mm的振幅下，不同频率的振幅图，如图7所示，从5.6hz开始，中间部分的能量回收装置1，可以产生125mm-125mm的振幅，到16.2hz之后，可以持续地产生125mm-125mm的振幅，证明双稳态结构在低频低振幅的外部激励下，可以拓宽能量回收装置的振幅。独立层式液态金属摩擦纳米发电机自身可以适应低频高振幅的振动激励环境，所以借助双稳态的势能函数关系，可以在振动过程中牺牲部分振动频率来充分利用外部的惯性力，从而提高能量回收装置1的振幅以及加速度，从而提高能量回收效率。

以上所述，仅为本发明较佳的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，根据本发明的技术方案及其发明构思加以等同替换或改变，都应涵盖在本发明的保护范围之内。