经验模态分解构造观测矩阵的方法与流程

本发明涉及矩阵技术领域，特别是涉及经验模态分解构造观测矩阵的方法。

背景技术：

压缩感知理论中，由于并不能预先知道k-稀疏信号x在其稀疏变换域中k个分量的具体位置。因此，观测矩阵φ往往被设计得更倾向于随机矩阵，使得测量具备普适性(测量通带宽)，才能保证x中的重要信息能被公平地测量到，才能大概率地保持信号信息的完整性。但是，随机性导致有用的信息并未被着重测量，而无用的信息被多次测量，这也是为了实现高精度重构，所需测量次数比k大很多的原因之一。同时，实际测量中因为压缩测量，能量不可避免地损失，而当能量损失到一定程度时，信息损失也不可避免。

理论上讲，由于高斯随机矩阵和伯努利随机矩阵中的元素都是独立同分布的，因此与任何信号或者正交基的相关性很小。经过学者证明，对于任意信号，这两种矩阵具有接近最优的观测性能，但是其缺点在于存储复杂度和计算复杂度。多年来，研究者们提出了多种观测矩阵，改进和优化主要面向：(1)能够达到尽量少的观测次数；(2)结构尽量简单、稀疏(降低存储和计算复杂度)；(3)易于硬件实现。改进型观测矩阵主要分为部分随机矩阵、结构化矩阵和确定性矩阵。典型的有：(1)局部傅里叶矩阵和局部哈达玛矩阵系列，这一系列矩阵的构造方式是随机选取正交变换矩阵的某些行，其优势在于每个矩阵元素都有固定的计算公式；(2)托普利兹矩阵和循环矩阵系列，这一系列矩阵将线性系统中的卷积以及循环卷积计算应用于观测矩阵设计，结构化矩阵在满足观测要求和降低随机性方面进行了折衷。(3)基于编码理论的低相关性确定性矩阵，确定性矩阵易于硬件实现，这一系列矩阵基于信源编码或信道编码中的数学工具，能保证设计的矩阵有很小的列相关性。但缺点在于受到复杂数学运算和各种约束，往往只能构造出维数比较小的矩阵。

研究表明，结合信号先验知识设计匹配的观测矩阵，使得恢复性能有明显提升：如果已有信号模板(如主动探测等应用)或有大量的相似训练信号(如诱发脑电等应用)，根据信号的特征指导观测矩阵的构造；又或以某个参量作为衡量标准，在观测过程中根据待测信号的变化进行自适应地调整，压缩感知的压缩性能应该可以得到提高；在压缩感知编码中若能够使用边信息(与待处理信号类似的信号)，利用该信息构造观测矩阵，可以大大减少测量次数；以微分熵来表征压缩感知解的可信度，以微分熵下降是否最快衡量在下一次迭代中所选的观测矩阵，该方法优化了观测矩阵，同等测量次数下比随机观测矩阵的重构性能有很大提高。

所以本发明提供一种新的基于信号先验知识设计观测矩阵的方案来解决此问题。

技术实现要素：

针对上述情况，为克服现有技术之缺陷，本发明基于信号特征来构造观测矩阵的思想，提出利用对参考信号进行经验模态分解(empiricalmodedecomposition,emd)后得到的本征模函数(intrinsicmodefunction,imf)，按照循环矩阵的形式构建压缩感知观测矩阵的方法。

其解决的技术方案是，经验模态分解构造观测矩阵的方法，首先设置一路参考信号，该参考信号与待处理的信号具有相同或相似的特征，然后对该参考信号进行emd分解，获得一组本征模函数后，按照循环矩阵的形式将本征模函数构造成所需的观测矩阵，具体实现步骤如下：

(1)对参考信号xr进行emd分解，得到一组本征模函数向量imf1～imfp；定义向量imf1表示为上标1表示第一个本征模函数向量，imfp表示为所有imf向量写成矩阵形式：

(2)将本征模函数通过整体循环扩充得到行数为m的本征模函数循环矩阵，整体循环的方法表示为：

由于以上技术方案的采用，本发明与现有技术相比具有如下优点：

(1)在利用压缩感知进行信号降噪应用中，为参考信号添加一定程度的噪声后形成的观测矩阵，对降噪有更佳的效果；

(2)在利用压缩感知进行信号降噪应用中，对于待处理的含噪信号与参考信号在时间基准有错位的情况，与传统随机观测矩阵相比，仍能够更好地凸显信号的频域特征，具有实用价值。

附图说明

图1为本发明经验模态分解构造观测矩阵的方法流程。

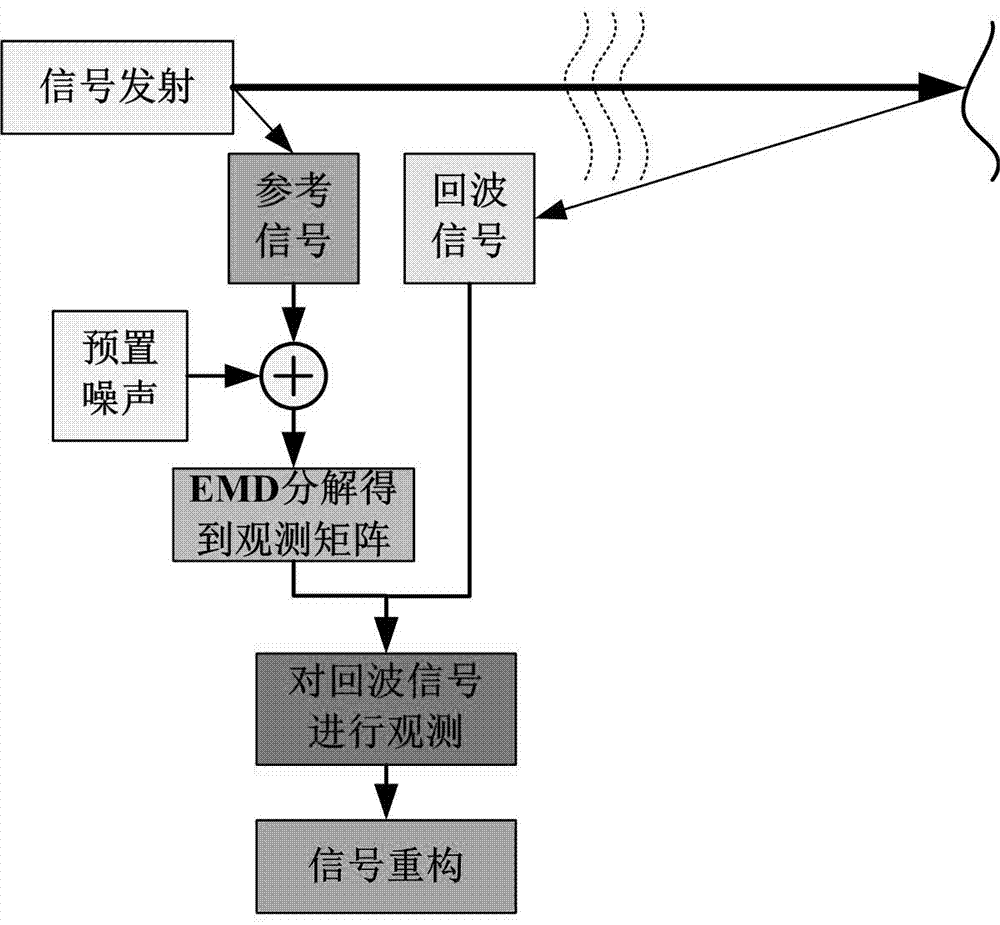
图2为本发明经验模态分解构造观测矩阵的方法典型应用场景。

图3为本发明经验模态分解构造观测矩阵的降噪效果图。

图4为本发明中的参考信号信噪比对降噪效果的影响图。

图5为本发明对与参考信号有时域错位的信号降噪效果图。

具体实施方式

有关本发明的前述及其他技术内容、特点与功效，在以下配合参考附图1至附图5对实施例的详细说明中，将可清楚的呈现。以下实施例中所提到的结构内容，均是以说明书附图为参考。

具体实施方式中的应用场景如附图2所示，应用场景为典型的主动探测系统。其中，参考信号取自发射信号，加入预置噪声后进行emd分解，用于构造imf循环矩阵作为压缩感知的观测矩阵。利用该观测矩阵对回波信号进行观测并进行信号重构，重构后的信号的信噪比有明显地提高。

为了验证本方法的可行性以及实际使用的效果，下面进行仿真分析验证本方法。

(1)回波信号与参考信号在时域严格对准。

以4种不同频率的正弦波合成1×n信号x，n＝256。试验中，以稀疏随机矩阵和高斯随机矩阵为对比，三种观测矩阵的观测次数和重构算法的迭代次数均一致。在降噪试验中，用awgn函数对x添加高斯白噪声后作为待降噪信号，信噪比为5db。imf循环矩阵的构造过程为：用awgn函数对x预置不同程度(5～20db)的高斯白噪声作为参考信号，分别进行emd分解，得到imf分量后根据测量次数m构造循环矩阵。附图3给出了参考信号信噪比15db时，不同观测矩阵的降噪效果。附图4给出了参考信号的不同信噪比对降噪效果的影响曲线。

由附图3可知，imf循环矩阵在较少测量次数时即有很好的降噪效果。参考信号信噪比会影响降噪效果，由附图4可知，无预置噪声并非是最好的选择，而是存在一个最佳信噪比，且该最佳的信噪比与测量次数相关。因为在某个信噪比时，emd分解后的imf同时包含了信号和噪声的特征，因此可以达到更好的降噪效果。

(2)回波信号与参考信号在时域上存在对准误差。

考虑到回波信号不可能与参考信号在时域上严格对准，在仿真时设置一个时域误差δ：采样点0～δ为随机噪声，采样点(δ+1)～n为含噪回波信号，利用高斯随机矩阵和稀疏随机矩阵作为对比，重构算法是正交匹配追踪算法。仿真中设置时域误差为采样点数δ＝20。发射信号x由200hz的载波通过50hz频率调制而成，用awgn函数对x添加高斯白噪声后作为待降噪的回波含噪信号，信噪比为-1db。参考信号信噪比20db，测量次数为80次，重构算法为正交匹配追踪算法。各阶段信号的频谱如附图5所示。随机矩阵对比实验中，回波信号没有时域误差。

由附图5可知，与理想情况相比，虽然imf循环矩阵对与参考信号有错位的信号在降噪效果上有所降低，但仍能够很好地保留信号的频域特征，抑制干扰信号的频域特征，可以视为实现了有效降噪，且在波形和频谱图上体现出降噪效果要明显优于随机矩阵。

本发明面向拥有待处理信号的先验知识的压缩感知应用(现有技术)，提出了利用对参考信号进行经验模态分解得到的本征模函数构造观测矩阵的方法——本征模函数循环矩阵。仿真结果表明：为参考信号添加一定程度的噪声后再进行emd分解，对于降噪有更佳的效果；在含噪信号与参考信号在时域完全对准的情况下，imf循环矩阵能够以较明显少于随机矩阵的测量次数达到更优的降噪效果；在含噪信号与参考信号在时域有错位的情况下，虽然降噪效果与理想情况有所降低，但是由频谱图发现，imf循环矩阵能够很好地凸显信号的频域特征。

以上所述是结合具体实施方式对本发明所作的进一步详细说明，不能认定本发明具体实施仅局限于此；对于本发明所属及相关技术领域的技术人员来说，在基于本发明技术方案思路前提下，所作的拓展以及操作方法、数据的替换，都应当落在本发明保护范围之内。